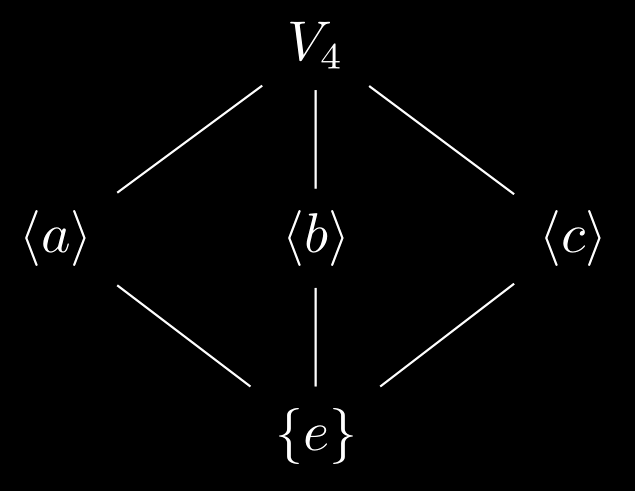Abstract Algebra: A Brief Summary of Group Theory

1. Basic axioms

Definition: binary operation

A binary operation $\star$ on a set $G$ is a function $\star$: $G\times G \to G$.

Note that for any $a,b\in G$, we shall write $a\star b $ for $\star(a,b)$.

1. A binary operation $\star$ on a set $G$ is associative if $\forall a,b,c \in G$, $a\star(b\star c) = (a\star b) \star c$.
2. If $\star$ is a binary operation on a set $G$,
   • we say $a,b\in G$ are commute if $a\star b =b\star a$;
   • we say $\star$ (or $G$) is commutative if $\forall a,b\in G$, $a\star b = b\star a$.

Examples: binary operation

• $+,\times$ are commutative binary operations on $\mathbb{Z}$ (or $\mathbb{Q}, \mathbb{R},\mathbb{C}$).
• $-$ is a noncommutative binary operation on $\mathbb{Z}$, where $a-b\neq b-a$.
• $-$ is not a binary operation on $\mathbb{Z}^{+}$ (nor $\mathbb{Q}^{+},\mathbb{R}^{+}$) because for $a,b\in\mathbb{Z}^{+}$, $a-b \notin \mathbb{Z}^{+}$ if $a < b $.

Definition: group

A group is an order pair $(G,\star)$ where $G$ is a set and $\star$ is a binary operation on $G$ satisfying the following axioms:

1. $\star$ is associative, i.e., $\forall a,b,c\in G$,$(a\star b)\star c = a\star (b\star c)$,
2. $\exists e \in G$ called identity, such that $\forall a\in G$, $a\star e =e \star a = a$,
3. $\forall a \in G$, $\exists a^{-1}\in G$ called inverse, such that $a\star a^{-1} = a^{-1}\star a =e$.

1. The group $(G,\star)$ is called abelian (or commutative) if $\forall a,b\in G$, $a\star b = b\star a$.
2. The group $(G,\star)$ is called finite if in addition $G$ is a finite set, otherwise it is infinite.

Examples: group

• $\mathbb{Z}, \mathbb{Q}, \mathbb{R}$ and $\mathbb{C}$ are groups under $+$ with $e=0$ and $\forall a, a^{-1}=-a$.
• $\mathbb{Q}-\qty{0},\mathbb{R}-\qty{0}, \mathbb{C}-\qty{0}$, $\mathbb{Q}^{+},\mathbb{R}^{+}$ are groups under $\times$ with $e=0$ and $\forall a, a^{-1}=\frac{1}{a}$.
• For $n\in\ZZ^+$, $\ZZ/n\ZZ$ is an abelian group under the operation $+$ of addition of residue classes/
• Fpr $n\in\ZZ^{+}$, the set $(\ZZ/n\ZZ)^{\times}$ of equivalence classes $\bar{a}$ which have multiplicative inverses mod $n$ is an abelian group under multiplication of residue classes.

For simplicity, we usually say $G$ is a group, but that doesn’t imply the set itself is a group, we still need to specify the binary operation $\star$. E.g., $(\mathbb{Z},+)$ is a group, but $(\mathbb{Z},\times)$ is not a group.

If $(A, \star)$ and $(B,\diamond)$ are groups, their direct product $A\times B$ is a new group, which means

\[\begin{equation} A \times B = \{(a,b) | a\in A,b\in B\}, \quad (a_1,b_1)(a_2,b_2) = (a_1\star a_2,b_1\diamond b_2). \end{equation}\]

Proposition

If $G$ is a group under the operation $\star$, then

1. the identity of $G$ is unique;
2. $\forall a\in G$, $a^{-1}$ is unique;
3. $\forall a \in G$, $(a^{-1})^{-1} = a$;
4. $\forall a,b\in G$, $(a\star b)^{-1} = (b^{-1})\star (a^{-1})$;
5. for any $a_1,a_2,\dots,a_n \in G$, $a_1 \star a_2\star \cdots \star a_n$ is independent of how the expression is bracketed (generalized associative law).

Proposition

Let $G$ (operation $\cdot$ will be omitted) be a group and $a,b\in G$. The equations $ax=b$ and $ya=b$ have unique solutions for $x,y\in G$. In particular,

1. if $au = av$ , then $u=v$;
2. if $ub=vb$, then $u=v$.

Definition: the order of a group and its element

For $G$ a group and $x\in G$, define the order of $G$ is its cardinality, i.e., the number of its elements, and denote this integer by $\abs{G}$. If $G$ is not finite, we say its order is infinite.

Define the order of $x$ to be the smallest positive integer $n$ such that $x^n=e$ and denote this integer by $\vert x\vert$, $x$ is said to be of order $n$.

If no positive power of $x$ is the identity, the order of $x$ is defined to be infinity and $x$ is said to be of infinite order. E.g., in the additive groups $\mathbb{Z},\mathbb{Q},\mathbb{R}$ or $\mathbb{C}$ every nonzero (i.e., nonidentity) element has infinite order.

Definition: group table.

Let $G = {g_1,g_2,\dots,g_n}$ be a finite group with $g_1= e$. The multiplication table or group table of $G$ is the $n\times n$ matrix whose $i,j$ entry is the group element $g_ig_j$.

\[\begin{array}{c|cccc} G & g_1 & g_2 & \cdots & g_i & \cdots & g_j & \cdots & g_n \\ \hline g_1 & g_1 g_1 & g_1g_2 & \cdots & g_1g_i &\cdots & g_1g_j & \cdots & g_1g_n \\ g_2 & g_2g_1 & g_2g_2 & \cdots & g_2g_i & \cdots & g_2 g_j & \cdots & g_2 g_n \\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \cdots\\ g_i & g_ig_1 & g_ig_2 & \cdots & g_ig_i & \cdots & g_i g_j& \cdots & g_ig_n \\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \cdots\\ g_j & g_jg_1& g_jg_2& \cdots & g_jg_i & \cdots & g_jg_j& \cdots & g_jg_n\\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \cdots\\ g_n & g_n g_1 & g_n g_2 & \cdots & g_n g_i & \cdots & g_n g_j & \cdots & g_n g_n \end{array}\]

2. Some specific groups

2.1. Dihedral groups

Definition: dihedral group

For $n\in\mathbb{Z}^{+}, n\geq 3$, the dihedral group $D_n$ is defined to be the group consisting of the symmetry actions of a regular $n$-gon, where the operation is composition of actions.

The group $D_n$ is a non-abelian group of order $2n$ ($n$ reflections and $n$ rotations totally).

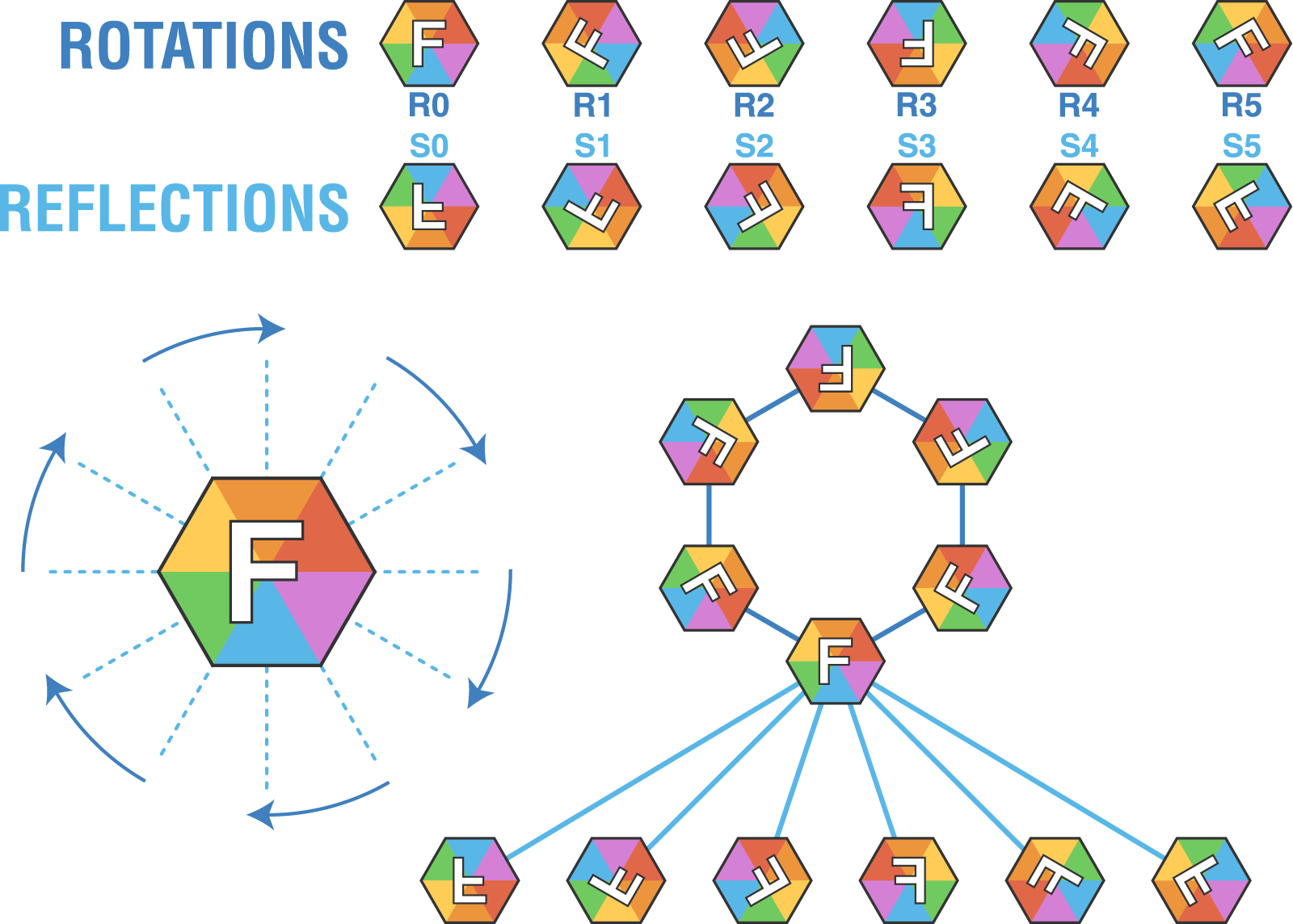The symmetry group of a regular hexagon consists of six rotations and six reflections. The six reflections consist of three reflections along the axes between vertices, and three reflections along the axes between edges. From hexnet.

Let $r$ be the rotation clockwise about the origin through $2\pi/n$ radian, $s$ be the reflection about the line of symmetry through vertex $1$ and the origin. Then

\[\begin{equation} D_{n} = \braket{r,s}{ r^n = s^2 = e, rs = sr^{-1}}, \end{equation}\]

where $r$ and $s$ are a set of generators of $D_{n}$.

2.2. Symmetric groups

Definition: symmetric group

1. For $\Omega \neq \emptyset$, $S_{\Omega}$ is defined to be the set of all bijections from $\Omega$ to itself (i.e., the set of all permutations of $\Omega$). The set of $S_{\Omega}$ is a group under function composition, and $S_{\Omega}$ is called the symmetric group on the set $\Omega$.
2. In the special case when $\Omega = \qty{1,2,\dots,n}$, the symmetric group on $\Omega$ is denoted $S_n$, the symmetric group of degree $n$, and $\abs{S_n} = n!$.

A cycle is a string of integers which represents the element of $S_n$ which cyclically permutes these integers (and fixes all other integers), i.e., the cycle $(a_1\ a_2\ \dots \ a_m)$ is the permutation which sends $a_i$ to $a_{i+1}$, $1\leq i \leq m-1$ and sends $a_m$ to $a_1$.

In general, for each $\sigma\in S_n$, it can be written as the following form

\[\begin{equation} \sigma = (a_1\ a_2\ \dots \ a_{m_{1}})(a_{m_1 +1} \ a_{m_1 + 2} \ \dots \ a_{m_2}) \dots (a_{m_{k-1}+1} a_{m_{k-1}+2}\cdots a_{m_k}), \end{equation}\]

which is called the cycle decomposition of $\sigma$.

The length of a cycle is the number of integers which appear in it. A cycle of length $t$ is called a $t$-cycle. A 2-cycle is called a transposition. Every element of $S_n$ may be written as a product of transpositions, i.e.,

\[\begin{equation} S_n = \langle T \rangle \quad \text{where $T= \qty{(i,j) \ | \ 1\leq i < j \leq n}$}. \end{equation}\]

Two cycles are called disjoint if they have no numbers in common. Disjoint cycles commute. The cycle decomposition of each permutation is the unique way of expressing a permutation as a product of disjoint cycles. The order of a permutation is the l.c.m. (least common multiple) of the lengths of the cycles in its cycle decomposition.

The identity permutation of $S_n$ is

\[\begin{equation} e = (1)(2)(3)\cdots(n). \end{equation}\]

Example: elements of $S_3$

Note that $|S_3| = 3! =6$, the cycle decomposition of 6 elements is $e$, $(2\ 3)$, $(1\ 3)$, $(1\ 2)$, $(1\ 2\ 3)$ and $(1\ 3\ 2)$.

Since $(1\ 2) \circ (1\ 3) = (1 \ 3 \ 2)$, $(1 \ 3)\circ(1\ 2) = (1\ 2\ 3)$, it shows that $S_n$ is a non-abelian group for all $n\geq 3$.

2.3. Matrix groups

Definition: field

A field is a set $F$ together with two binary operations $+$ and $\cdot$ on $F$ such that $(F,+)$ is an abelian group (call its identity $0$) and ($F - \qty{0},\cdot$) is also an abelian group, and the following distributive law holds:

\[\begin{equation} a\cdot(b+c) = (a\cdot b) + (a\cdot c) , \quad \forall a,b,c \in F. \end{equation}\]

For any field $F$ let $F^{\times} = F- {0}$.

Definition: general linear group

Let $F$ be a field, then the general linear group $GL_n(f)$ is the group of invertible $n\times n$ with entries in $F$ under matrix multiplication.

If $F$ is a finite field, then $GL_n(F)$ has only finitely many elements:

• if $F$ is a field and $\vert F \vert <\infty$, then $\abs{F} = p^{m}$ for some prime $p$ and integer $m$;
• if $F = q <\infty$, then $\abs{GL_n(F)} = \prod_{k=0}^{n-1}(q^n - q^k)$.

2.4. The quaternion group

Definition: the quaternion group

The quaternion group, $Q_8$ is defined by

\[\begin{equation} Q_8 = \{e,-e,i,-i,j,-j,k,-k\},\quad \text{where $i^2 = j^2 = k^2=ijk=-e$}. \end{equation}\]

Note that $Q_8$ is a non-abelian group of order $8$.

3. Homomorphisms and isomorphisms

3.1. Homomorphisms

Definition: homomorphism

Let $(G,\star)$ and $(H,\diamond)$ be groups. A map $\varphi:G\to H$ such that

\[\begin{equation} \varphi(x\star y) = \varphi(x) \diamond \varphi(y) ,\quad \forall x,y,\in G \end{equation}\]

is called a homomorphism. In cases where no confusion arises, we always write $\varphi(xy) = \varphi(x)\varphi(y)$.

Proposition

Let $G$ and $H$ be groups and let $\varphi:G\to H$ be a homomorphism.

1. $\varphi(e_{G})= e_H$.
2. $\varphi(g^{-1}) = \varphi(g)^{-1}, \forall g\in G$.
3. $\varphi(g^n) = \varphi(g)^n, \forall n \in \ZZ$.

• The image of a homomorphism $\varphi:G\to H$, denoted by $\mathrm{im}\ \varphi$, is simply the image of $\varphi$ as a map of sets

  \[\begin{equation} \mathrm{im}\ \varphi = \qty{h\in H \ \vert\ h = \varphi(g), \forall g\in G}. \end{equation}\]

• The kernel of a homomorphism $\varphi:G\to H$, is the set of elements of $G$ that are mapped to the identity in $H$:

  \[\begin{equation} \mathrm{ker}\ \varphi = \qty{g\in G \ \vert\ \varphi(g) = e_{H}}. \end{equation}\]

Examples: homomorphism

• Let $G$ be any group, let $H=\qty{e}$ and define $\varphi: G\to H$ by $\varphi(g)=1$, for all $g\in G$. This map is trivial homomorphism and $\mathrm{ker}\ \varphi = G$.
• Let $G = \RR^2$ (operation vector addition), let $H = \RR$ (operation addition) and define $\varphi: \RR^2\to \RR$ by $\varphi((x,y)) = x$ which means projection onto the $x$-axis. Then $\varphi$ is a homomorphism. And $\mathrm{ker}\ \varphi = \qty{(x,y)\vert x=0}$ is the $y$-axis.

• Let $G= Q_8$ and let $H=V_4$ be the Klein $4$-group. Define $\varphi:Q_8\to V_4$ by

  \[\varphi(\pm 1) = 1,\quad \varphi(\pm i) = a,\quad \varphi(\pm j) = b,\quad \varphi(\pm k) =c.\]

  Then $\varphi$ is a homomorphism and $\mathrm{ker}\ \varphi = \qty{\pm 1}$.

3.2. Isomorphisms

Definition: isomorphism

Let $(G,\star)$ and $(H,\diamond)$ be groups. A map $\varphi:G\to H$ is called an isomorphism and $G$ and $H$ are said to be isomorphic or of the same isomorphism type, written $G \cong H$, if

1. $\varPhi$ is a homomorphism (i.e., $\varphi(xy) = \varphi(x)\varphi(y)$ where the group operations are not explicitly written), and
2. $\varphi$ is a bijection.

Examples: isomorphism

• For any group $G$, $G\cong G$.
• The exponential map exp : $\mathbb{R}\to\mathbb{R}^{+}$ defined by $\exp(x) = \mathrm{e}^{x}$, $\RR \to \RR^+$ is an isomorphism from $(\RR,+)$ to $(\RR,\times)$, since $\e^{x+y} = \e^x+\e^y$.
• Let $\triangle,\Omega\neq \emptyset$, then $S_{\triangle}\cong S_{\Omega} \Leftrightarrow \abs{\triangle} = \abs{\Omega}$.

4. Subgroups

4.1. Definition of subgroup

Definition: subgroup

Let $G$ be a group. The subset $H\subset G$ is a subgroup of $G$ if $H\neq \emptyset$ and $H$ is closed under product and inverses. Note that the binary operation of $H$ is the same as $G$.

• If $H$ is a subgroup of $G$ we shall write $H\leq G$.
• If $H\leq G$ and $H\neq G$ we shall write $ H < G $ .

Examples: subgroup

• Any group $G$ has two subgroups: $H=G$ and $H = \qty{e}$; the latter is called the trivial subgroup.
• $\ZZ \leq \QQ$ and $\QQ\leq \RR$ with the operation of addition.
• Let $H = \qty{1,r,r^2,\dots,r^{n-1}}$, then $H\leq D_n=\expval{r,s}$.
• Let $G$ and $H$ be groups and let$\varphi:G\to H$ be a homomorphism, then $\mathrm{im} \ \varphi\leq H$, $\mathrm{ker}\ \varphi \leq G$.
• If $K\leq H$ and $H\leq G$, then $K\leq G$.

Proposition: the subgroup criterion

A subset $H$ of a group $G$ is a subgroup if and only if

1. $H\neq \emptyset$, and
2. $\forall x,y\in H$, $xy^{-1}\in H$.

4.2. Centralizers and normalizers, stabilizers and kernels

Definition: centralizer

Define $C_{G}(A) = \qty{g\in G \vert gag^{-1} = a, \forall a\in A}$. This subset $C_{G}(A)$ of $G$ is called the centralizer of $A$ in $G$.

Definition: center

Define $Z(G) = \qty{g\in G\vert gx=xg, \forall x\in G}$, the set of elements commuting with all the elements of $G$. This subset $Z(G)$ of $G$ is called the center of $G$.

Definition: normalizer

Define $gAg^{-1} = \qty{gag^{-1}\vert \forall a\in A}$. Define the normalizer of $A$ in $G$ to be the set $N_{G}(A) = \qty{g\in G \vert gA g^{-1} = A}$.

Proposition

1. $C_{G}(A) \leq G$;
2. $Z(G) = C_{G}(G)\leq G$;
3. $C_{G}(A)\leq N_{G}(A)\leq G$.

Examples: centralizer and normalizer

1. If $G$ is abelian, then $Z(G)=G$. And $C_{G}(A)=N_{G}(A) = G$ for any $A \subset G$.
2. Let $G = D_4$, $A=\qty{e,r,r^2,r^3}$, then $C_{D_4}(A)=A$, $N_{D_4}(A)= D_4$ and $Z(D_4) = \qty{1,r^2}$.
3. Let $G= S_3$, $A=\qty{1,(1\ 2)}$, then $C_{S_3}(A) = N_{S_3}(A)= A$ and $Z(S_3) = \qty{e}$.

Definition: stabilizer

If $G$ is a group acting on a set $S$ and $s$ is some fixed element of $S$, the stabilizer of $s$ in $G$ is the set $G_{s} = \qty{g\in G \vert g\cdot s =s}$ and $G_{s}\leq G$.

Definition: kernel

Define the kernel of the action of $G$ on a set $S$ to be the set $\qty{g\in G \vert g\cdot s = s, \forall s\in S}$, and it is also a subgroup of $G$.

4.3. Cyclic groups and cyclic subgroups

Definition: cyclic groups

A group $H$ is cyclic if $H$ can be generated by a single element, i.e., $H = \qty{x^n | n\in \ZZ} = \expval{x}$, where $x$ os a generator of $H$.

Examples: cyclic group

• $(\ZZ,+) = \expval{1} = \expval{-1} = \qty{n\cdot 1 \vert n \in \ZZ}$.
• $(\ZZ_n,+) = \expval{1} = \qty{m\cdot 1 \vert 0\leq m < n }$. Note that $\ZZ_n \cong \ZZ/ n \ZZ$

Proposition

1. If $H = \expval{x}$, then $\abs{H} = \abs{x}$.
2. Let $G$ be an arbitrary group, $x\in G$ and let $m,n\in \ZZ$. If $x^n=e$ and $x^m=e$, then $x^d = e$, where $d=(m,n)$. In particular, if $x^m=e$ for some $m\in Z$, then $\abs{x}$ divides $m$.

Theorem: any two cyclic groups of the same order are isomorphic

Any two cyclic groups of the same order are isomorphic. More specifically,

1. if $n\in\mathbb{Z}^{+}$ and $\abs{\expval{x}} = \abs{\expval{y}} = n $, then the map

   \[\begin{equation}\varphi: \expval{x}\to \expval{y}, \quad x^k \mapsto y^ k. \end{equation}\]

   is well defined and is an isomorphism.

2. if $\expval{x}$ is an infinite cyclic group, the map

   \[\begin{equation} \varphi: \mathbb{Z} \to \expval{x}, \quad k\mapsto x^k. \end{equation}\]

   is well defined and is an isomorphism.

The following two propositions determine precisely which powers of $x$ generate the group $\expval{x}$.

Proposition

Let $G$ be a group, let $x\in G$ and let $a \in \ZZ-\qty{0}$

1. If $\abs{x}=\infty$, then $\abs{x^a} = \infty$.
2. If $\abs{x} = n <\infty$ , then $\abs{x^a} = \frac{n}{(n,a)}$.
3. In particular, if $\abs{x} = n < \infty$ and $a$ is a positive integer dividing $n$ (i.e., $a\vert n$), then $\abs{x^a} = \frac{n}{a}$.

Proposition

Let $H = \expval{x}$.

1. Assume $\abs{x} = \infty$. Then $H = \expval{x^a}$ if and only if $a=\pm 1$.
2. Assume $\abs{x} = n<\infty$. Then $H=\expval{x^a}$ if and only if $(a,n)=1$. In particular, the number of generators of $H$ is $\varphi(n)$ (where $\varphi$ is Euler’s $\varphi$-function).

Theorem: complete subgroup structure of a cyclic group

Let $H=\expval{x}$ be a cyclic group.

1. Every subgroup of $H$ is cyclic.
2. If $\abs{H} = \infty$, then for any $a\neq b$ and $a,b \in \ZZ^{+}$, $\expval{x^a}\neq \expval{x^b}$.
3. If $\abs{H} = n < \infty$, then for any $a >0$ and $a\vert n$, there is a unique subgroup of $H$ of order $a$. It is $\expval{x^d}$, where $d = \frac{n}{a}$. Furthermore, for $m\in \ZZ$, $\langle x^m\rangle = \langle x^{(n,m)}\rangle$.

Examples: subgroups of $\ZZ/12\ZZ$

Note that $\ZZ/12\ZZ$ is a cyclic group of order 12, and

\[\ZZ/12\ZZ = \expval*{\bar{1}} = \expval*{\bar{5}} = \expval*{\bar{7}} = \expval*{\bar{11}}, \quad \varphi(12)=4.\]

The subgroups of $\ZZ/12\ZZ$ are:

1. \(\expval*{\bar{2}} = \expval*{\bar{10}}\) (order $6$);
2. \(\expval*{\bar{3}} = \expval*{\bar{9}}\) (order $4$);
3. \(\expval*{\bar{4}} = \expval*{\bar{8}}\) (order $3$);
4. \(\expval*{\bar{6}}\) (order $2$);
5. \(\expval*{\bar{0}}\) (order $1$).

The inclusions between them are given by

\[\expval*{\bar{a}} \leq \expval*{\bar{b}}, \quad \text{if and only if $(b,12)\vert (a,12)$}, \quad 1\leq a,b\leq 12.\]

4.4. Subgroups generated by subsets of a group

Proposition

Let $G$ be a group, if $\mathcal{A}$ is any nonempty collection of subgroups of $G$, then $K = \displaystyle{\bigcap_{H\in \mathcal{A}}} H \leq G$.

In the above proposition, let $\mathcal{A}=\qty{H\leq G \vert A \subseteq H}$, we can get a special subgroup:

Definition: subgroup generated by subsets of a group

If $A$ is any subset of the group $G$, define

\[\begin{equation} \expval{A} = \bigcap_{\substack{A\subseteq H\\ H\leq G}} H. \end{equation}\]

This is called the subgroup of $G$ generated by $A$. Note that $\expval{A}$ is the smallest subgroup of $G$ containing $A$.

Proposition

If $A$ is any subset of the group $G$, then

\[\begin{equation} \expval{A} = \qty{a_1^{\alpha_1}a_2^{\alpha_2}\cdots a_{n}^{\alpha_n}\vert \text{for each $i$, $a_i \in A,\alpha_i \in \ZZ, a_i \neq a_{i+1}$ and $n \in \ZZ^{+}$} }. \end{equation}\]

Furthermore, if $A$ is the finite subset $\qty{a_1,a_2,\dots,a_k}$ of the abelian group $G$, then

\[\begin{equation} \expval{A} = \qty{a_1^{\alpha_1} a_2^{\alpha_2}\cdots a_n ^{\alpha_n} \vert \text{$\alpha_i \in \ZZ$ for each $i$}}. \end{equation}\]

4.5. The lattice of subgroups of a group

Given a group $G$, the lattice of subgroups of $G$ is the partially ordered set whose elements are the subgroups of $G$ with the partial order relation being set inclusion. It is common to depict the subgroup lattice for a group using a Hasse diagram, which is constructed as follows:

1. Each subgroup $H$ of $G$ is a vertes;
2. Plot all subgroups of $G$ starting at the bottom with $\qty{e}$, ending at the top with $G$;
3. Vertices corresponding to subgroups with smaller order are placed lower in the diagram than vertices corresponding to subgroups with larger order.
4. Draw paths upwards between subgroups using the rule that there will be a line upward from $A$ to $B$ if $A\leq B$ and there are no subgroups properly between $A$ and $B$.

Let $G$ be a group and $H,K\leq G$:

• $H\cap K \leq G$. Moreover, $H\cap K$ is the largest subgroup contained in both $H$ and $K$.
• $\expval{H,K} \leq G$. Moreover, $\expval{H,K}$ is the smallest subgroup containing both $H$ and $K$.

Meet and join for subgroups $H$ and $K$.

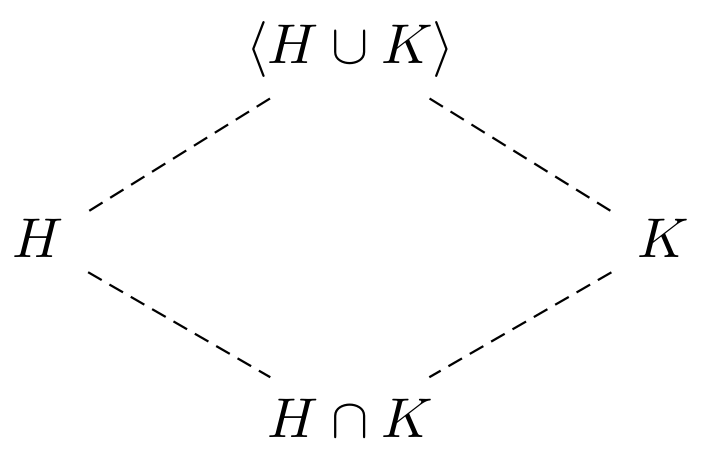
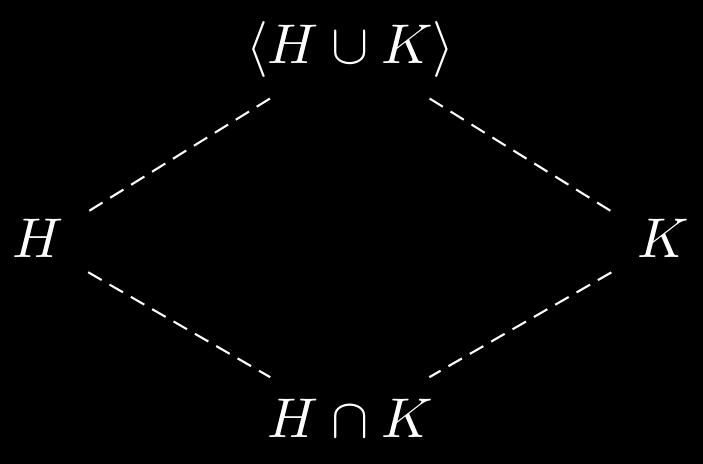
Note that isomorphic groups have the same lattices, but nonisomorphic groups may also have identical lattices.

Hasse diagram of the lattice of subgroups of the dihedral group Dih4, with the subgroups represented by their cycle graphs, from wiki

Examples: lattice of subgroups

• Some specific examples for lattice of subgroups of cyclic groups:

Subgroup lattice of some specific cyclic groups.

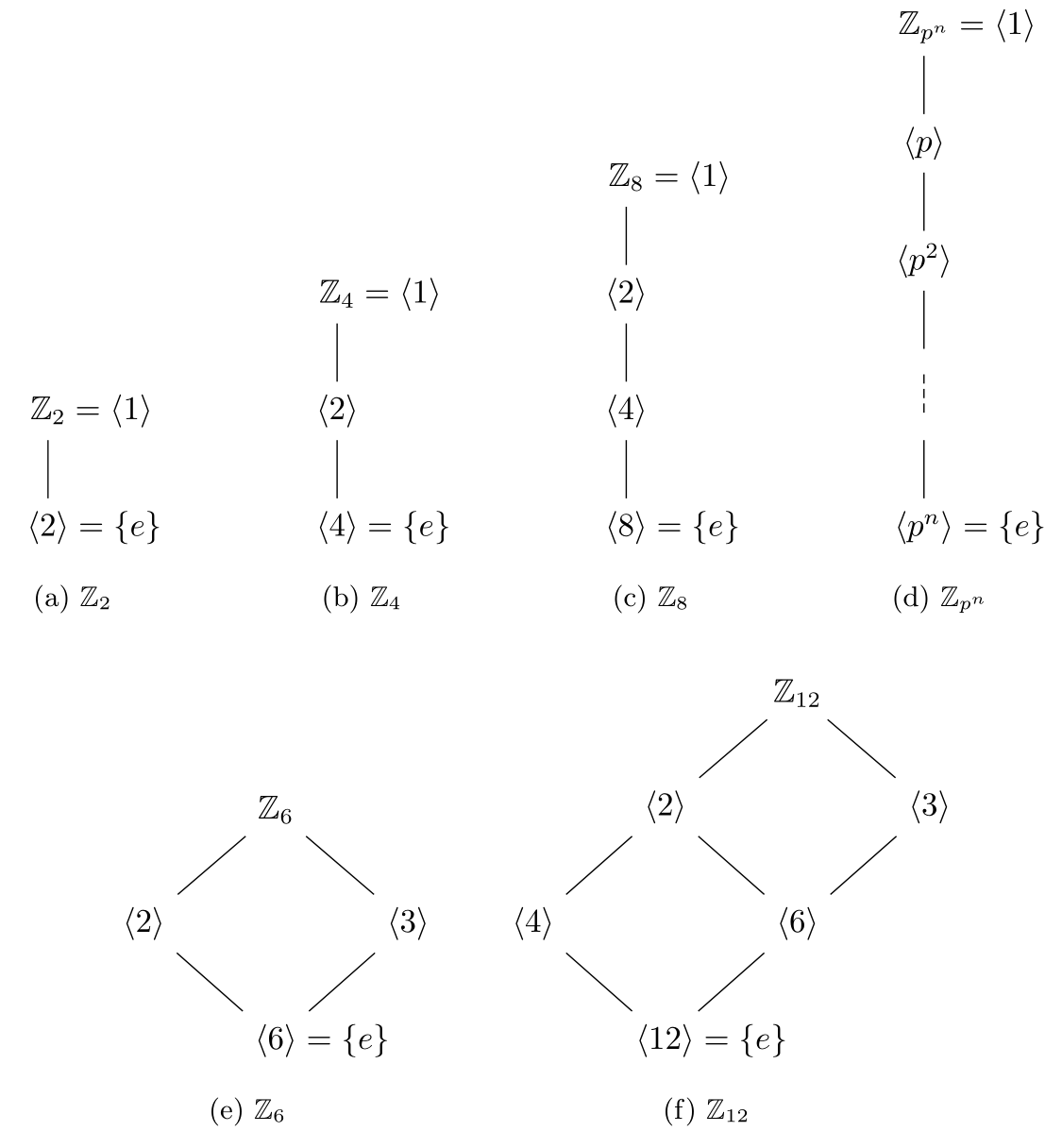
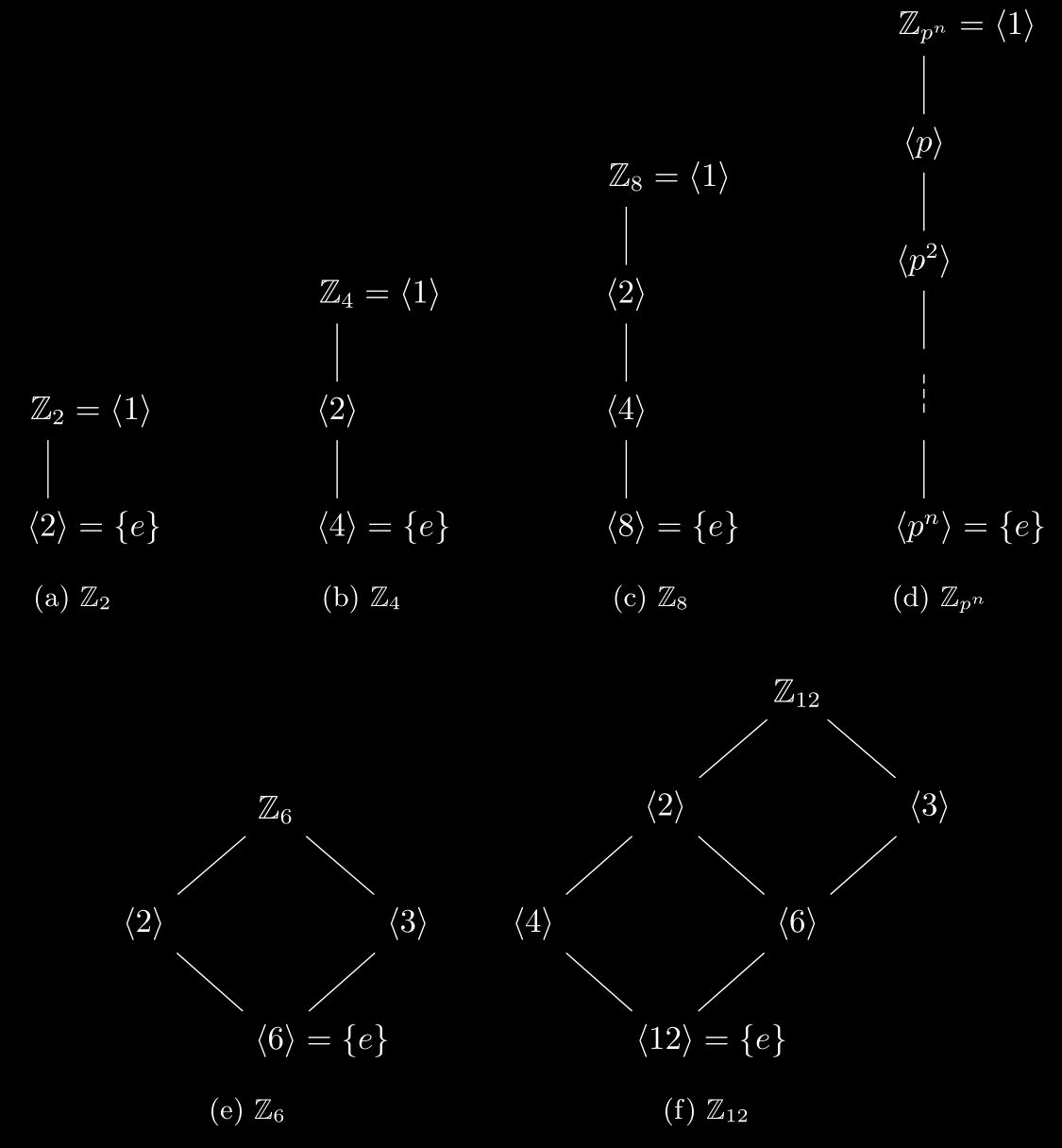
TikZ code

\usepackage{mathtools, amsfonts,tikz-cd}
\newcommand{\lr}[1]{\langle#1\rangle}
\def\ZZ{\mathbb{Z}}

% ------------- Z_2 -----------------------
\begin{tikzcd}[arrows=dash]
   \ZZ_2 \mathrlap{{}=\lr{1}} \ar[d] & \\
   \lr{2} \mathrlap{{}= \{e\}}
\end{tikzcd}

% ------------- Z_4 -----------------------
\begin{tikzcd}[arrows=dash]
   \ZZ_4 \mathrlap{{}=\lr{1}} \ar[d] & \\
   \lr{2} \ar[d]&\\
   \lr{4} \mathrlap{{}= \{e\}}
\end{tikzcd}

% ------------- Z_8 -----------------------
\begin{tikzcd}[arrows=dash]
   \ZZ_8 \mathrlap{{}=\lr{1}} \ar[d] & \\
   \lr{2} \ar[d]&\\
   \lr{4} \ar[d]&\\
   \lr{8} \mathrlap{{}= \{e\}}
\end{tikzcd}

% ------------- Z_p^n -----------------------
\begin{tikzcd}[arrows=dash]
   \ZZ_{p^n} \mathrlap{{}=\lr{1}} \ar[d]\\
   \lr{p} \ar[d]&\\
   \lr{p^2} \ar[d]&\\
   \ar[d,dashed]&\\[-0.2cm]
   \ar[d]&\\
   \lr{p^{n}} \mathrlap{{}= \{e\}}
\end{tikzcd}

% ------------- Z_6 -----------------------
\begin{tikzcd}[arrows=dash]
   &\ZZ_6 \ar{dl}\ar{dr} \\
   \lr{2} \ar{dr} & &  \lr{3} \ar{dl} \\
   &\lr{6} \mathrlap{{}= \{e\}}
\end{tikzcd}

% ------------- Z_12 -----------------------
\begin{tikzcd}[column sep={4em,between origins},arrows=dash]
    && \ZZ_{12} \ar{dl}\ar{dr} \\
    &\lr{2} \ar{dl} \ar{dr}& &  \lr{3} \ar{dl} \\
    \lr{4} \ar{dr} & &   \lr{6}=\{e\} \ar{dl}\\
    & \lr{12} \mathrlap{{}= \{e\}}&
\end{tikzcd}

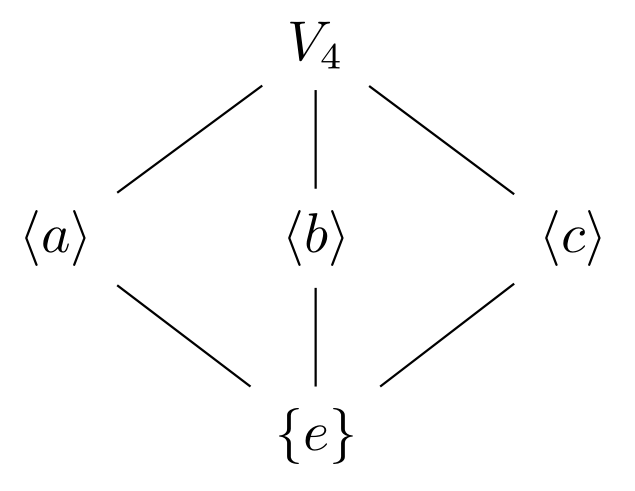
• The lattice of the Klein 4-group (Vierruppe), $V_4=\expval{a,b,c\vert a^2=b^2=c^2=e}$:

Subgroup lattice of $V_4$.

TikZ code

\usepackage{mathtools, amsfonts,tikz-cd}
\newcommand{\lr}[1]{\langle#1\rangle}

\begin{tikzcd}[arrows=dash]
    & V_4 \ar[ld] \ar[d] \ar[rd]\\
    \lr{a}\ar[rd]& \lr{b} \ar[d] & \lr{c} \ar[ld]\\
    &e
\end{tikzcd}

• The lattice of $S_3$:

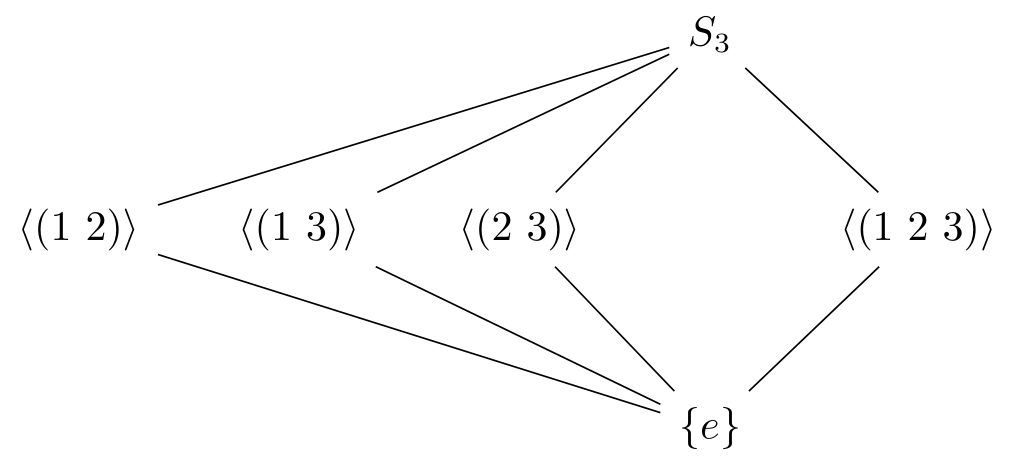
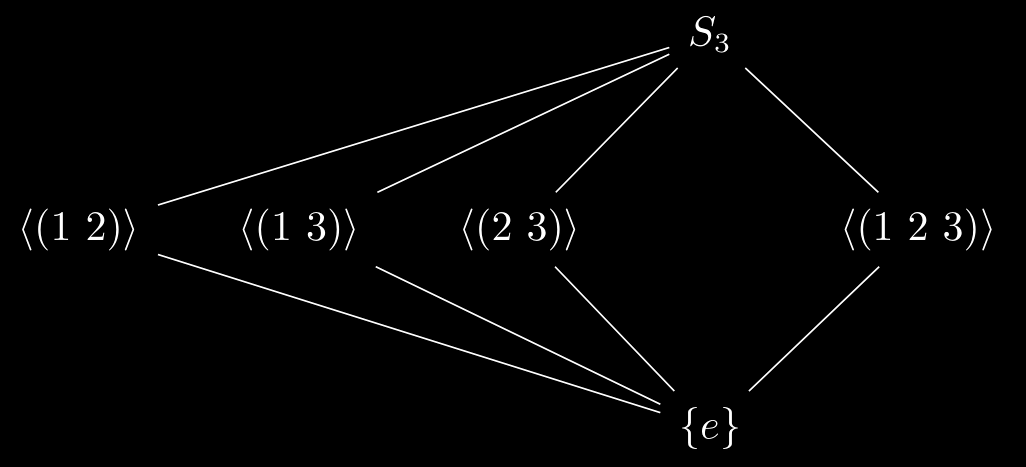
Subgroup lattice of $S_3$.

TikZ code

\usepackage{mathtools, amsfonts,tikz-cd}
\newcommand{\lr}[1]{\langle#1\rangle}

\begin{tikzcd}[arrows=dash]
    &&& S_3 \ar[llld] \ar[lld] \ar[ld] \ar[rd]\\
    \lr{(1\ 2)}\ar[rrrd]& \lr{(1\ 3)} \ar[rrd] & \lr{(2\ 3)}\ar[rd] & &\lr{(1\ 2\ 3)} \ar[ld]\\
    &&&\{e\}
\end{tikzcd}

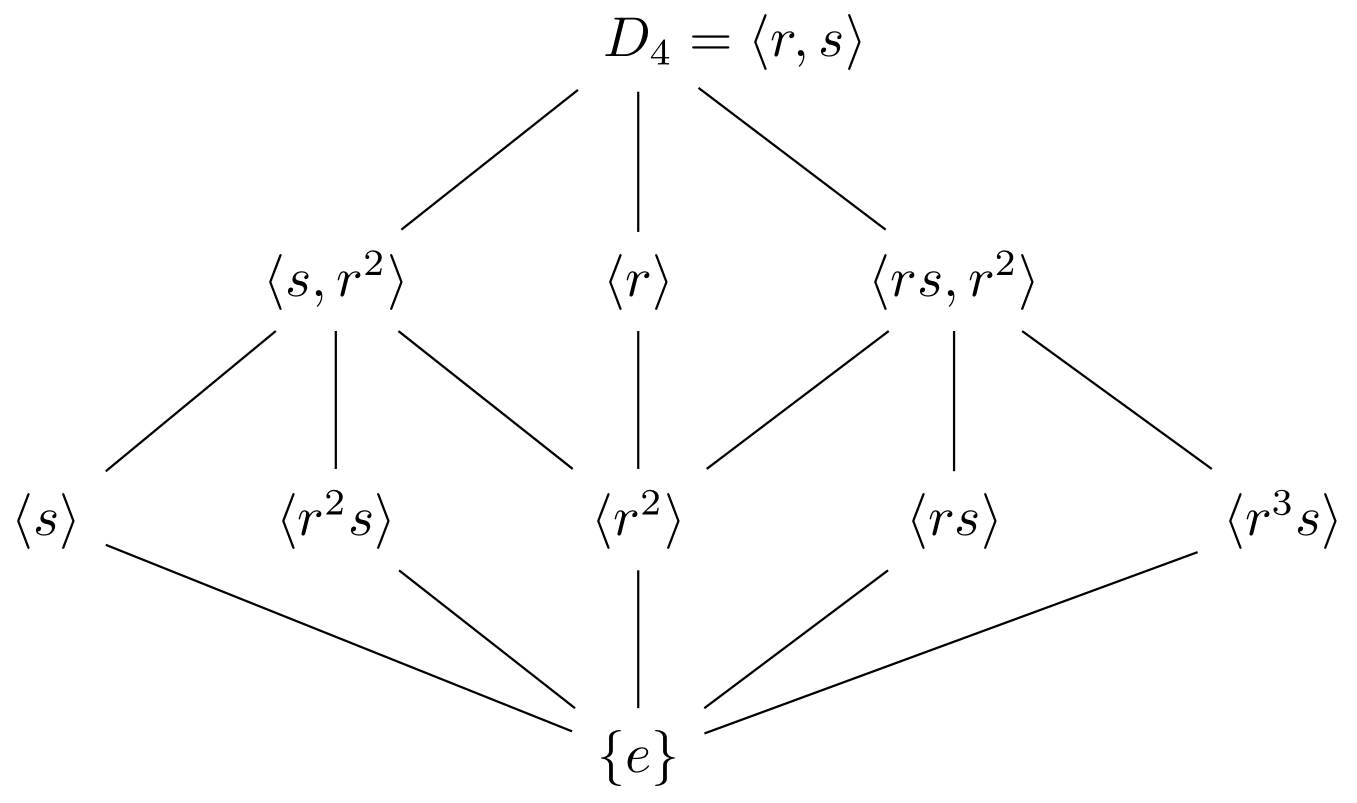
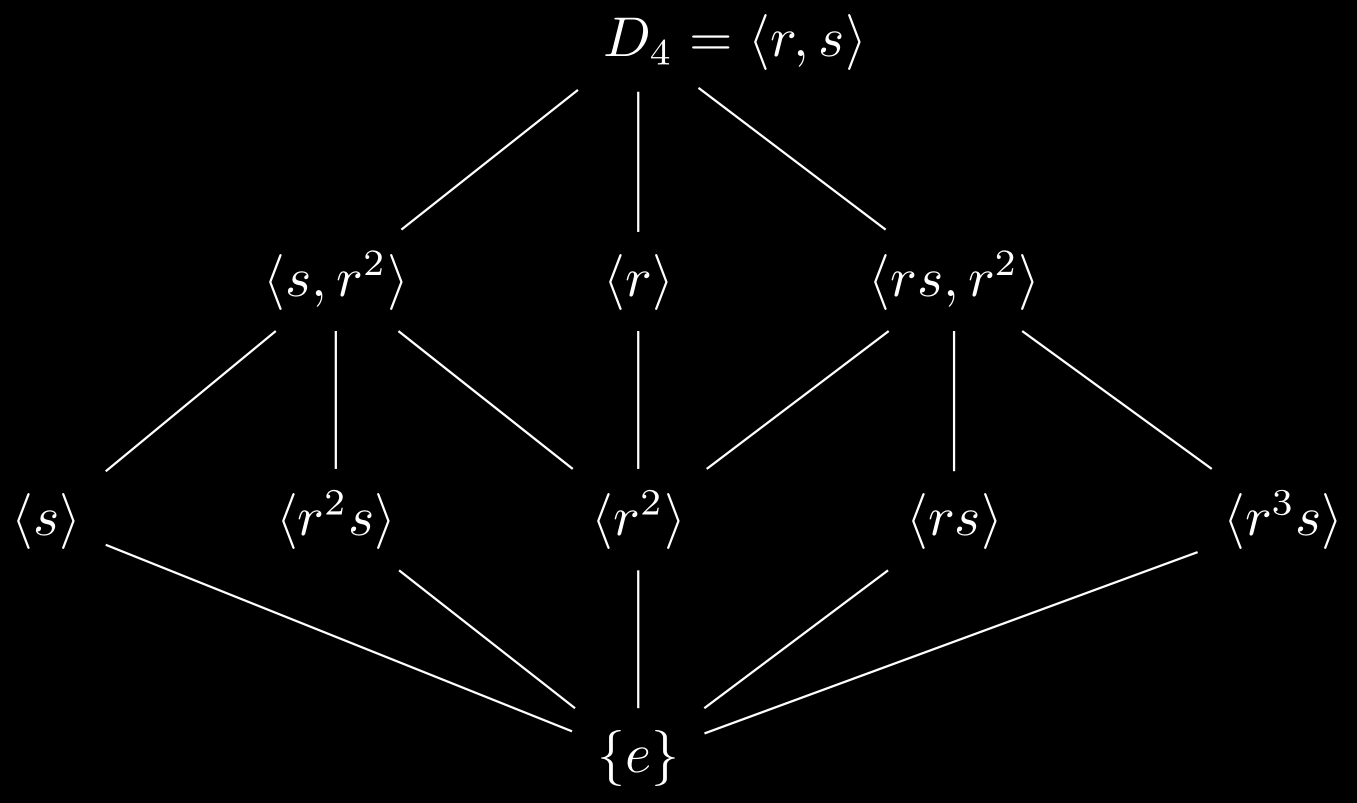
• The lattice of $D_4 = \expval{r,s}$:

Subgroup lattice of $D_4$.

TikZ code

\usepackage{mathtools, amsfonts,tikz-cd}
\newcommand{\lr}[1]{\langle#1\rangle}

\begin{tikzcd}[row sep=2.5em,arrows=dash]
    &&D_4\mathrlap{{}=\lr{r,s}} \ar[ld] \ar[d] \ar[rd]\\
    &\lr{s,r^2}\ar[ld]\ar[d]\ar[rd]&  
    \lr{r}\ar[d] 
    &\lr{rs,r^2}\ar[ld]\ar[d]\ar[rd]\\
    \lr{s}\ar[rrd]& \lr{r^2s}\ar[rd] &\lr{r^2} \ar[d]&\lr{rs}\ar[ld] & \lr{r^3s}\ar[lld]\\
    &&\{e\}
\end{tikzcd}

• The lattice of $Q_8$:

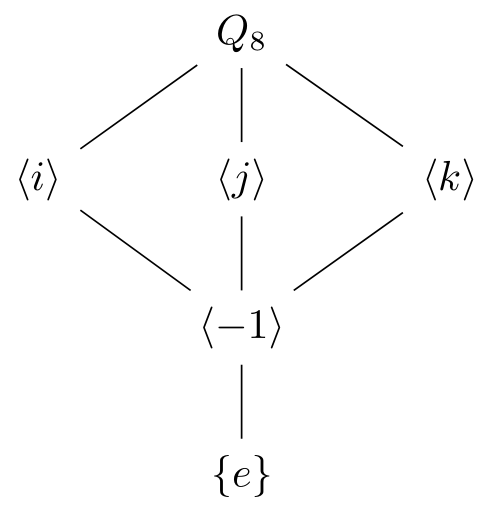
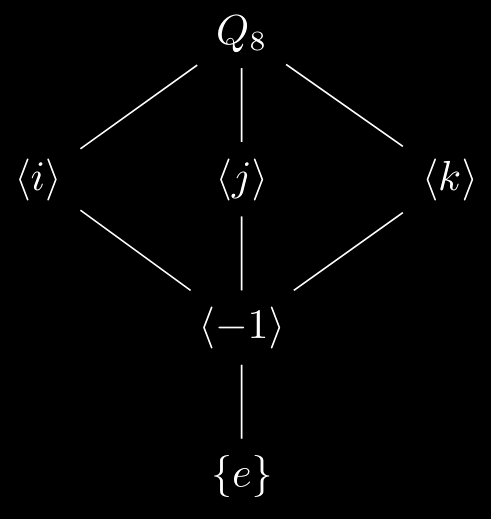
Subgroup lattice of $Q_8$.

TikZ code

\usepackage{mathtools, amsfonts,tikz-cd}
\newcommand{\lr}[1]{\langle#1\rangle}

\begin{tikzcd}[arrows=dash]
    &Q_8 \ar[ld] \ar[d] \ar[rd]\\
    \lr{i}\ar[rd]&  \lr{j}\ar[d] &\lr{k}\ar[ld]\\
    &\lr{-1}\ar[d]\\
    &\{e\}
\end{tikzcd}

• The lattice of $D_8$:

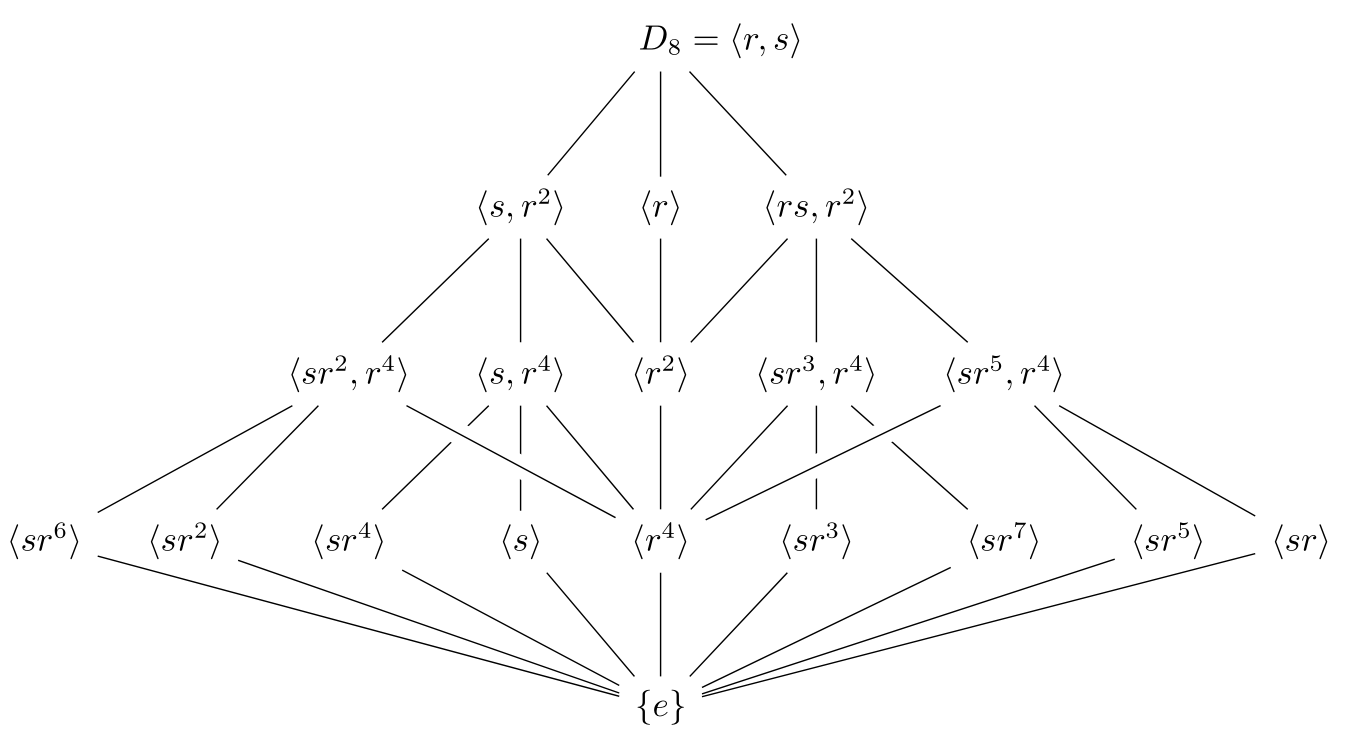
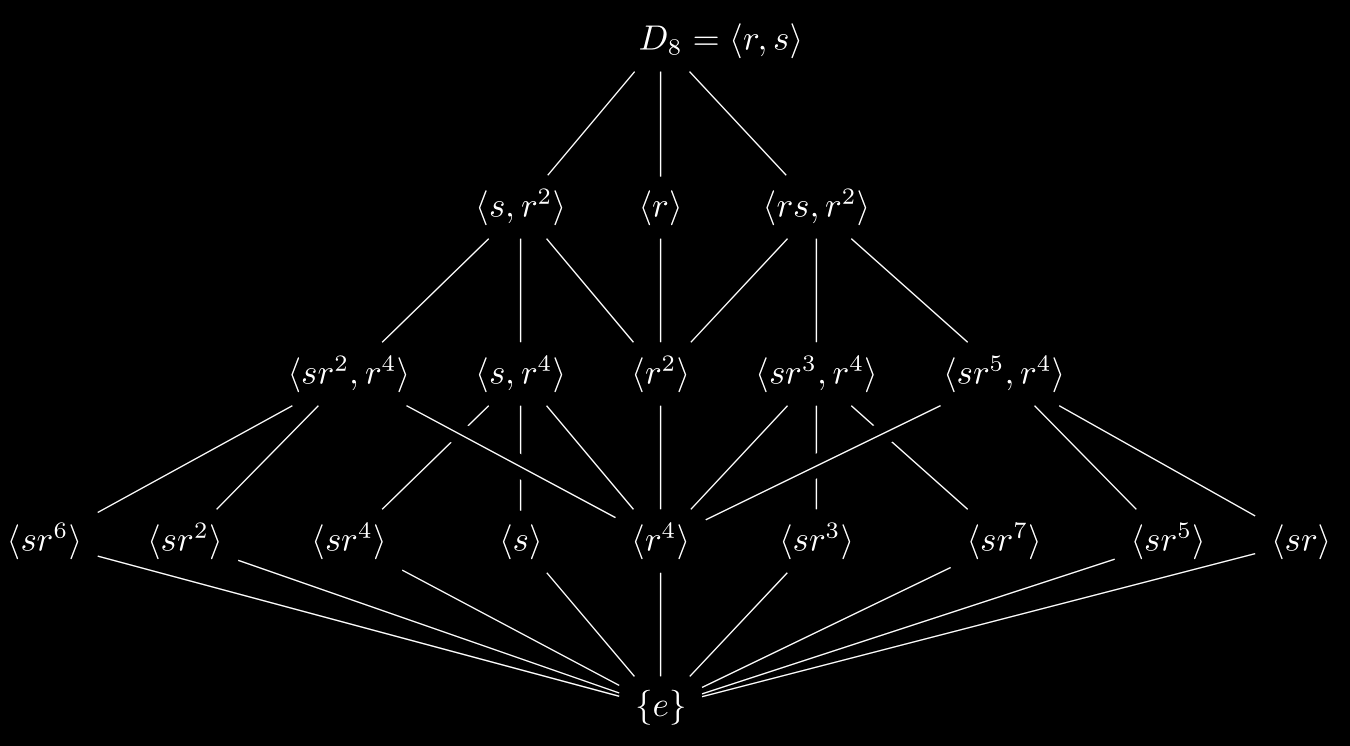
Subgroup lattice of $D_8$.

TikZ code

\usepackage{mathtools, amsfonts,tikz-cd}
\newcommand{\lr}[1]{\langle#1\rangle}

\begin{tikzcd}[row sep=3em,column sep=1em,arrows=dash]
    &&&&D_8\mathrlap{{}=\lr{r,s}} \ar[ld]\ar[d]\ar[rd]&\\
    &&&\lr{s,r^2}\ar[ld]\ar[d]\ar[rd]&  \lr{r}\ar[d] &\lr{rs,r^2}\ar[ld]\ar[d]\ar[rd]\\
    &&\lr{sr^2,r^4}\ar[lld]\ar[ld]\ar[rrd]&\lr{s,r^4}\ar[ld]\ar[d]\ar[rd] & \lr{r^2}\ar[d] & \lr{sr^3,r^4} \ar[ld]\ar[d]\ar[rd] & \lr{sr^5,r^4}\ar[lld]\ar[rd]\ar[rrd]\\
    \lr{sr^6}\ar[rrrrd]&\lr{sr^2}\ar[rrrd]& \lr{sr^4}\ar[rrd]& \lr{s}\ar[rd] & \lr{r^4}\ar[d] & \lr{sr^3}\ar{ld} & \lr{sr^7}\ar[lld]& \lr{sr^5}\ar[llld] & \lr{sr}\ar[lllld]\\
    &&&&\{e\}
    \arrow[from=3-3,to=4-5,crossing over]
    \arrow[from=3-7,to=4-5,crossing over]
\end{tikzcd}

4.6. Cosets and Lagrange’s theorem

Definition: coset

Let $G$ be a group and $H$ a subgroup of $G$.

1. Define a left coset of $H$ with representative $g\in G$ to be the set

   \[\begin{equation} g H = \qty{gh\ \vert\ \forall h\in H }. \end{equation}\]

2. Define a right coset of $H$ with representative $H g$ to be the set

   \[\begin{equation} H g = \qty{hg \ \vert \ \forall g\in H} \end{equation}\]

Examples: coset

Let $H$ be the subgroup of $S_3$ defined as $\qty{(1),(1\ 2\ 3), (1\ 3\ 2)}$.

• The left cosets of $H$ are

\[\begin{gather*} (1) H = (1\ 2\ 3) H = (1\ 3\ 2) H = \qty{(1),(1\ 2\ 3), (1\ 3\ 2)},\\[.2cm] (1\ 2) H = (1\ 3) H = (2\ 3) H = \qty{(1\ 2), (1\ 3), (2\ 3)}. \end{gather*}\]

• The right cosets of $H$ are

\[\begin{gather*} H(1) = H(1\ 2\ 3) = H(1\ 3\ 2) = \qty{(1),(1\ 2\ 3), (1\ 3\ 2)},\\[.2cm] H(1\ 2) = H(1\ 3) = H(2\ 3) = \qty{(1\ 2), (1\ 3), (2\ 3)}. \end{gather*}\]

Let $K$ be the subgroup of $S_3$ defined as $\qty{(1),(1\ 2)}$.

• The left cosets of $K$ are

\[\begin{gather*} (1)K = (1\ 2) K = \qty{(1),(1\ 2)},\\[.2cm] (1\ 3) K = (1\ 2\ 3) K =\qty{(1\ 3), (1\ 2\ 3)},\\[.2cm] (2\ 3) K = (1\ 3\ 2) K = \qty{(2\ 3),(1\ 3\ 2)}. \end{gather*}\]

• The right cosets of $K$ are

\[\begin{gather*} K (1) = K (1\ 2) = \qty{(1),(1\ 2)},\\[.2cm] K (1\ 3) = K (1\ 3\ 2) =\qty{(1\ 3), (1\ 3\ 2)},\\[.2cm] K (2\ 3) = K (1\ 2\ 3) = \qty{(2\ 3),(1\ 2\ 3)}. \end{gather*}\]

Let $H$ be a subgroup of a group $G$ and suppose that $g_1,g_2\in G$. The following conditions are equivalent:

1. $g_1 H= g_2 H$;
2. $H g_1^{-1} = H g_2 ^{-1}$;
3. $g_1 H \subset g_2 H$;
4. $g_2 \in g_1 H$;
5. $g_1^{-1} g_2 \in H$.

Proposition

Let $H$ be a subgroup of a group $G$. Then the left (right) cosets of $H$ in $G$ partition $G$. That is, the group $G$ is the disjoint union of the left (right) cosets of $H$ in $G$.

Define the index of $H$ in $G$ to be the number of left cosets of $H$ in $G$, denoted as $[G: H]$. Note that the number of left cosets of $H$ in $G$ is the same as the number of right cosets of $H$ in $G$.

Theorem: Lagrange's theorem

Let $G$ be a finite group and let $H$ be a subgroup of $G$. Then $\abs{G}/\abs{H} = [G:H]$. In particular, the number of elements in $H$ must divide the number of elements in $G$.

Proof

Based on our preview proposition, we can deduce that $G$ can be expressed in the following form:

\[G = (g_1 H)\cup (g_2 H) \cup \cdots \cup (g_{l} H),\]

where $g_i H$, $i=1,2,\dots,l$ are the disjoint left cosets of $H$. However, there is a map between $H$ and any coset of $H$ is bijective. Let $K$ be a left coset of $H$ in $G$. Then there is a $g\in G$ such that $K=gH$. Define $\phi : H\to K$ by $\phi(h) = g h $.

1. $\phi$ is one to one. If $h_1\neq h_2$, then with cancellation $gh_1\neq g h_2$, so $\phi(h_1)\neq \phi(h_2)$.
2. $\phi$ is onto. If $k \in K$, then there is an $h\in H$ such that $k=g h$. It follows that $\phi(h) = k$ and as $k$ was arbitrary, $\phi$ is onto.

So the cardinality of each of these cosets is the same as the order of $H$, then

\[\abs{G} = \abs{H} + \abs{H} + \cdots + \abs{H} = l \cdot \abs{H},\ \Rightarrow \ \abs{G}/\abs{H} = [G: H]\]

∎

There are some corollaries of Lagrange’s theorem:

1. Suppose that $G$ is a finite group and $g\in G$. Then $\abs{g} \mid \abs{G}$.
2. Let $\abs{G} = p$ with $p$ a prime number. Then $G$ is cyclic, i.e., $G\cong \ZZ_{p}$. And any $g\in G$ such that $g\neq e$ is a generator.
3. Let $H$ and $K$ be subgroups of a finite group $G$ such that $K\subset H \subset G$. Then

\[\begin{equation} [G: K ] = [G: H] [H:K]. \end{equation}\]

Theorem: Cauchy's theorem

If $G$ is a finite group and $p$ is a prime dividing $\abs{G}$, then $G$ has an element of order $p$.

Theorem: Sylow's theorem

If $G$ is a finite group of order $p^{\alpha} m$, where $p$ is a prime and $p$ does not dive $m$, then $G$ has a subgroup of order $p^{\alpha}$.

Proposition

Let $H$ and $K$ be subgroups of a group $G$ and define

\[\begin{equation} HK = \qty{hk \ \vert \ h\in H, k\in K}. \end{equation}\]

1. If $H$ and $K$ are finite, then

   \[\begin{equation} \abs{HK} = \frac{\abs{H}\abs{K}}{\abs{H\cap K}}. \end{equation}\]
2. $HK$ is a subgroup if and only if $HK=KH$.
3. If $H\leq N_{G}(K)$, then $HK\leq G$. In particular, if $K\trianglelefteq G$ then $HK\leq G$ for any $H \leq G$.
4. If $A \subset N_{G}(K)$, we shall say $A$ normalizes $K$.
5. If $A \subset C_{G}(K)$, we shall say $A$ centralizes $K$.

5. Normal subgroups and Quotient groups

5.1. Definition of normal subgroup and quotient group

Definition: normal subgroup

A subgroup $N$ of a group $G$ is normal in $G$ if $g N = Ng$ for all $g\in G$. That is, a normal subgroup of a group $G$ is one in which the right and left cosets are precisely the same.

If $N$ is a normal subgroup of $G$, we shall write $N \trianglelefteq G$.

Examples: normal subgroup

• Any group $G$ has two trivial normal subgroups $N= G$ and $N=\qty{e}$. If $G$ has only trivial normal subgroups, it is called a simple group.
• Let $G$ be an abelian group, every subgroup $N$ of $G$ is a normal subgroup.
• Let $G$ be a group and $N\leq G$, if $[G:N] = 2$, then $N\trianglelefteq G$.

We can also define normal subgroup $N$ of $G$ as $gN g^{-1} = N$ for all $g\in G$. The element $g ng^{-1}$ is called the conjugate of $n\in N$ by $g$. The set $gNg^{-1}$ is called the conjugate of $N$ by $g$. So the normal subgroup is invariant under conjugation by members of the group of which it is a part.

Let $N$ be a subgroup of the group $G$. The following are equivalent:

1. $N\trianglelefteq G$;
2. $N_{G}(N)=G$;
3. $gN= Ng$, for all $g\in G$;
4. $gN g^{-1} \subseteq N$, for all $g\in G$.

Note that normal subgroups do not have transitivity. For example, $\expval{s}\trianglelefteq \expval{s,r^2}$ and $\expval{s,r^2}\trianglelefteq D_8$ but $\expval{s}\ntrianglelefteq D_8$ because $rsr^{-1} = sr^2 \notin \expval{s}$.

Definition: quotient group

Let $G$ be a group and $N \trianglelefteq G$, then the cosets of $N$ in $G$ form a group $G/N$ under the operation $(aN)(bN) = abN$. This group is called the factor or quotient group of $N$ in $G$ and read “$G$ modulo $N$”.

We can immediately write:

\[\begin{equation} |G| = |G/N| |N| \end{equation}\]

Examples: quotient group

• If $N \leq Z(G)$, then $N\trianglelefteq G$. In particular, $Z(G)\trianglelefteq G$.

• Consider the normal subgroup of $S_3$, $N=\qty{(1),(1\ 2\ 3), (1\ 3 \ 2)}$. The cosets of $N$ in $S_3$ are $N$ and $(1\ 2)N$. The factor group $S_3/N$ has the following multiplication table:

  \[\begin{array}{c|cc} S_3/N & N& (1\ 2)N\\[.2cm] \hline N & N & (1\ 2)N\\[.2cm] (1\ 2) N & (1\ 2)N & N \end{array}\]

  So $S_3/ N \cong \mathbb{Z}_2$.

Definition: natural projection

Let $N\trianglelefteq G$. The homomorphism $\pi: G \to G/N$ defined by $\pi(g) = gN$ is called the natural projection (homomorphism) of $G$ onto $G/N$. The kernel of this homomorphism is $N$.

5.2. The isomorphism theorems

Theorem: the first isomorphism theorem

If $\varphi:G\to H$ is a homomorphism of groups, then $\mathrm{ker}\ \varphi \trianglelefteq G$ and $G/ \mathrm{ker}\ \varphi \cong \varphi(G)$.

Theorem: the second or diamond isomorphism theorem

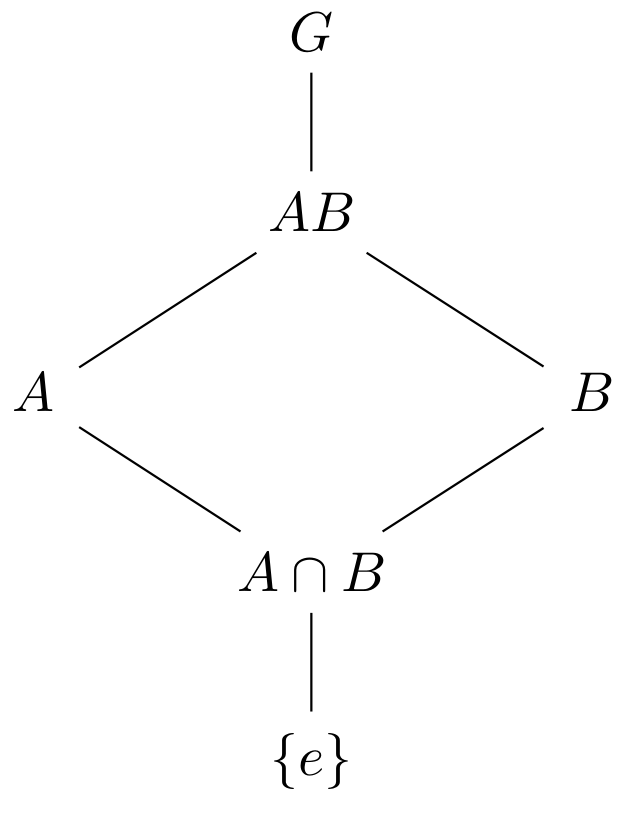
Let $G$ be a group, let $A$ and $B$ be subgroups of $G$ and assume $A \leq N_{G}(B)$. Then $AB$ is a subgroup of $G$, $B \trianglelefteq AB$, $A\cap B \trianglelefteq A$ and $AB/B \cong A/ A\cap B$.

Proof

We will first prove that $AB$ is a subgroup of $G$. Suppose that $a_1b_1,a_2b_2 \in AB$. Since $A\leq N_{G}(B)$, there must exist $b_3 \in B$ so that $b_1 a_2 = a_2 b_3$. Then

\[a_1 b_1 a_2 b_2 = a_1 a_2 b_3 b_2 = (a_1 a_2) (b_3b_2) \in AB.\]

and there must exist $b_4 \in B$ so that $a_1 b_1^{-1}a^{-1} = b_4$, then

\[(a_1 b_1)^{-1} = b_1^{-1} a_{1}^{-1} = a_1^{-1} a_1 b_1 a_{1}^{-1} = a_1^{-1} b_4 \in AB.\]

So $AB \leq G$. Since $A \leq N_{G}(B)$ and $B\leq N_{G}(B)$, it follows that $AB\leq N_{G}(B)$, i.e., $B$ is a normal subgroup of the subgroup $AB$, then the quotient group $AB/B$ is well defined. Define the map $\varphi:A \to AB/B$ by $\varphi(a) = aB$ and $\varphi$ is a homomorphism since

\[\varphi(a_1a_2) = (a_1a_2)B = a_1 B \cdot a_2 B = \varphi(a_1) \varphi(a_2).\]

For the second equal sign, we take advantage of the properties of cosets. Alternatively, the map $\varphi$ is just the restriction to the subgroup $A$ of the natural projection homomorphism $\pi: AB\to AB/B$, so is also a homomorphism. And $\varphi$ is surjective, the identity in $AB/B$ is the coset $e B$, so the kernel of $\varphi$ consists of the elements $a\in A$ with $aB=e B$, i.e., $\mathrm{ker} \ \varphi = A\cap B$. By the first isomorphism theorem, $A\cap B\trianglelefteq A$ and $A/A\cap B\cong AB/B$.

∎

Subgroup lattice (looks like a diamond).

Theorem: the third isomorphism theorem

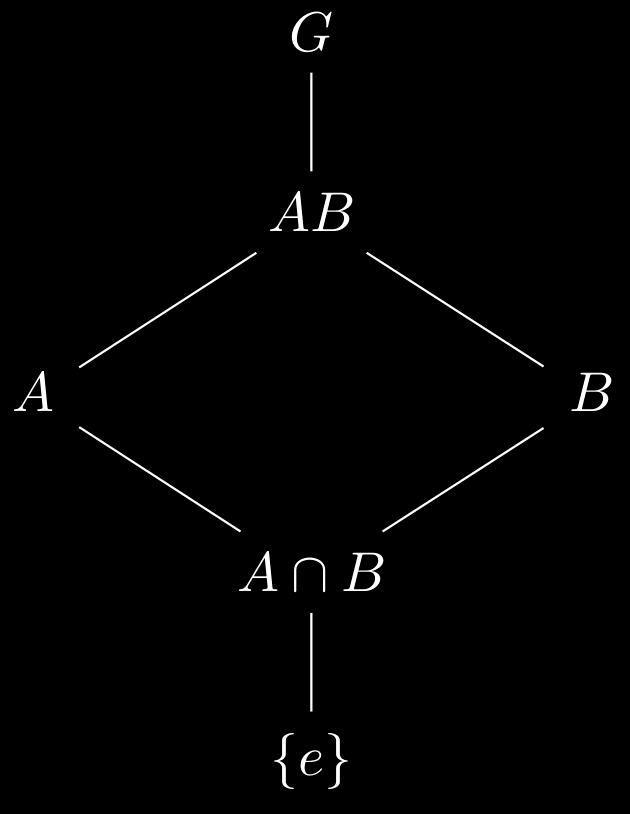
Let $G$ be a group and let $H\trianglelefteq G, K\trianglelefteq G$ with $H\leq K$. Then $K/H\trianglelefteq G/H$ and

\[\begin{equation} (G/H)(K/H) \cong G/K. \end{equation}\]

Proof

Note that $gH \in G/H$, $kH\in K/H$ for all $g\in G, k\in K$. Then $(gH)( kH) (g^{-1}H) = (gkg^{-1})H \in KH $, since $K\trianglelefteq G$. So $K/H\trianglelefteq G/H$.

Then note that $H \trianglelefteq K$. Define $\varphi: G/H \to G/K$ by $\varphi(gH) = gK$. Then we show $\varphi$ is well-defined. Suppose $g_1 H = g_2 H$, then $g_2^{-1} g_1 \in H$. Since $H\leq K$, then $g_2^{-1}g_1 \in H$ and so $g_1 K = g_2 K$, i.e., $\varphi(g_1H) = \varphi(g_2 H)$. Since $g$ may be chosen arbitrarily in $G$, $\varphi$ is a surjective homomorphism. Finally,

\[\begin{align*} \mathrm{ker}\ \varphi & = \qty{g H \in G/H \ | \ \varphi(gH) = e_G K}\\[.2cm] & = \qty{gH\in G/H\ | \ gK = e_{G}K}\\[.2cm] & = \qty{gH\in G/H\ | \ g\in K} = K/H. \end{align*}\]

By the first isomorphism theorem, $(G/H)/(K/H) \cong G/K$.

∎

Theorem: the fourth or lattice isomorphism theorem

Let $G$ be a group and let $N \trianglelefteq G$. Then there is a bijection from the set of subgroups $A$ of $G$ which contain $N$ onto the set of subgroups $\bar{A} = A/N$ of $G/N$.

In particular, every subgroup of $\bar{G}$ is of the form $A/N$ for some subgroup $A$ of $G$ containing $N$ (namely, its preimage in $G$ under the natural projection homomorphism from $G$ to $G/N$). This bijection has the following properties: for all $A,B \leq G$ with $N\leq A$ and $N\leq B$,

1. $A\leq B$ if and only if $\bar{A} \leq \bar{B}$,
2. if $A\leq B$, then $\abs{B:A} = \abs{\bar{B} : \bar{A}}$,
3. $\overline{\expval{A,B}} = \langle\bar{A},\bar{B}\rangle$,
4. $\overline{A\cap B} = \bar{A}\cap \bar{B}$, nd
5. $A \trianglelefteq G$ if and only if $\bar{A} \trianglelefteq G$.

This theorem tell us, the natural projection homomorphism $G\to G/N$ defines a bijective correspondence between the set of subgroups of $G$ containing $N$ and the set of (all) subgroups of $G/N$. If we regard $N$ as $e$ (this is of course true in $G/N$), then the lattice for $G/N$ (or rather, an isomorphic copy) appears in the lattice for $G$ as the collection of subgroups of $G$ between $N$ and $G$.

Examples: isomorphic copy

In the following examples, we use double lines to show the subgroup lattice of the quotient group.

• Let $G=Q_8$ and let $N$ be the normal subgroup $\expval{-1}$. Note that $Q_8/\expval{-1} \cong V_4$.

Subgroup lattice of $Q_8$ and the double lines give the lattice of $Q_8/\langle -1\rangle$.

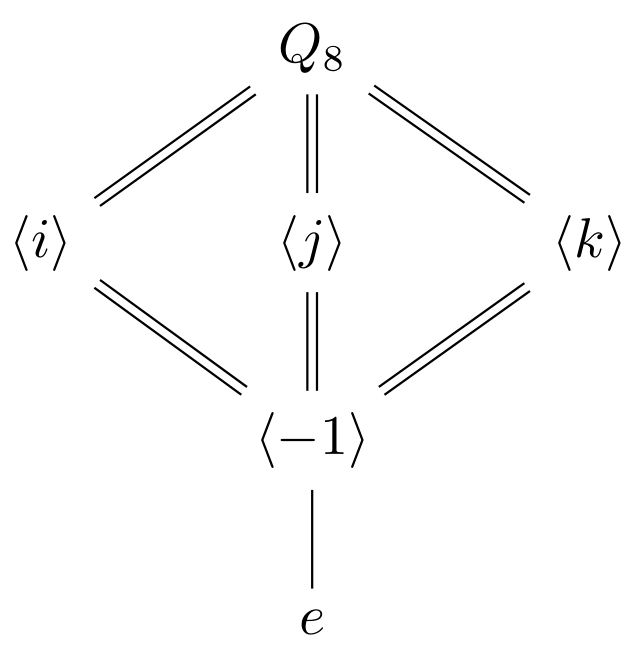
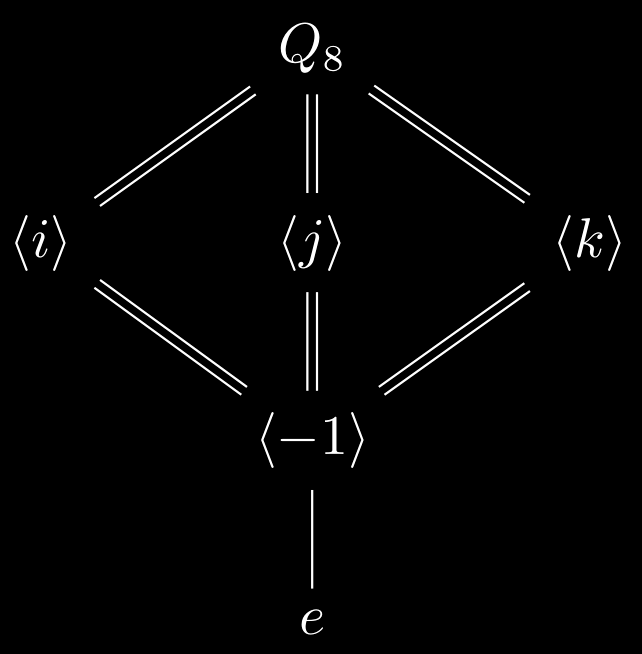
TikZ code

\usepackage{mathtools, amsfonts,tikz-cd}
\newcommand{\lr}[1]{\langle#1\rangle}

\begin{tikzcd}[arrows=dash]
    & Q_8 \ar[ld,shift right=0.2ex]\ar[ld,shift left=0.2ex] \ar[d,shift right=0.2ex]\ar[d,shift left=0.2ex] \ar[rd,shift left=0.2ex]\ar[rd,shift right=0.2ex]\\
    \lr{i}\ar[rd,shift right=0.2ex]\ar[rd,shift left=0.2ex]& \lr{j} \ar[d,shift right=0.2ex]\ar[d,shift left=0.2ex] & \lr{k}\ar[ld,shift left=0.2ex]\ar[ld,shift right=0.2ex]\\
    &\lr{-1}\ar[d]\\
    &e
\end{tikzcd}

• Let $G=D_4$ and $N$ be the normal subgroup $\expval{r^2}$. Note that $D_4/\expval{r^2} \cong V_4$.

Subgroup lattice of $D_4$ and the double lines give the lattice of $D_4/\langle r^2\rangle$.

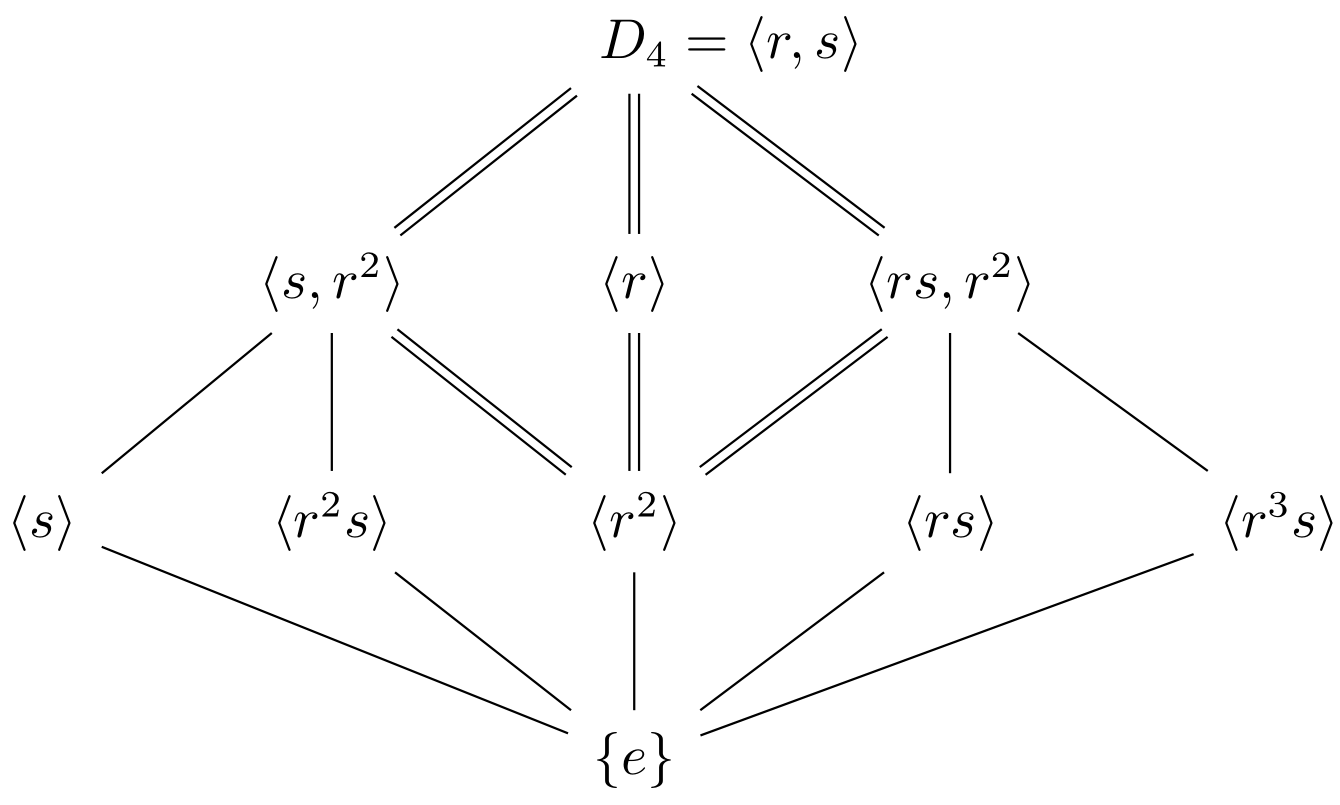
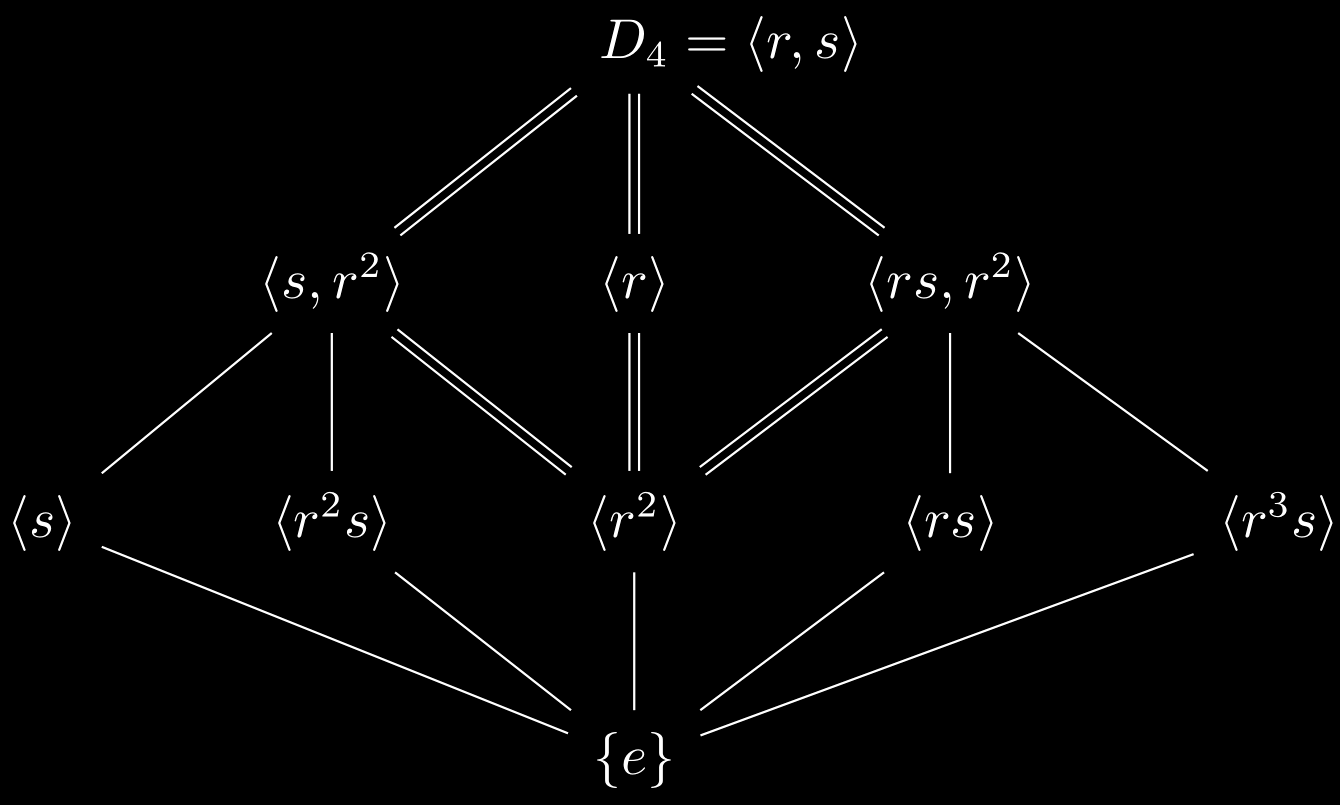
TikZ code

\usepackage{mathtools, amsfonts,tikz-cd}
\newcommand{\lr}[1]{\langle#1\rangle}

\begin{tikzcd}[row sep=2.5em,arrows=dash]
    &&D_4\mathrlap{{}=\lr{r,s}} \ar[ld,shift left=.2ex]\ar[ld,shift right=.2ex] \ar[d,shift left=.2ex]\ar[d,shift right=.2ex] \ar[rd,shift right=.2ex]\ar[rd, shift left=.2ex]\\
    &\lr{s,r^2}\ar[ld]\ar[d]\ar[rd,shift right=.2ex]\ar[rd, shift left=.2ex]&  
    \lr{r}\ar[d,shift left=.2ex]\ar[d,shift right=.2ex]
    &\lr{rs,r^2}\ar[ld,shift left=.2ex]\ar[ld,shift right=.2ex]\ar[d]\ar[rd]\\
    \lr{s}\ar[rrd]& \lr{r^2s}\ar[rd] &\lr{r^2} \ar[d]&\lr{rs}\ar[ld] & \lr{r^3s}\ar[lld]\\
    &&\{e\}
\end{tikzcd}

5.3. Hölder program

Definition: composition series

In a group $G$ a sequence of subgroups

\[\qty{e} = N_0 \leq N_1 \leq N_2 \leq \cdots \leq N_{k-1} \leq N_k =G.\]

is called a composition series if $N_i \trianglelefteq N_{i+1}$ and $N_{i+1}/N_i$ a simple group (i.e., there is no non-trivial normal subgroup), $0\leq i\leq k-1$. If the above sequence is a composition series, the quotient groups $N_{i+1}/N_i$ are called composition factors of $G$.

Example: composition series

For example,

\[\qty{e} \trianglelefteq \langle s \rangle \trianglelefteq \langle s,r^2 \rangle \trianglelefteq D_4 \quad \text{and} \quad \qty{e} \trianglelefteq \langle r^2\rangle \trianglelefteq \langle r \rangle \trianglelefteq D_4.\]

are two composition series for $D_4$ and in each series there are $3$ composition factors, each of which is isomorphic to (the simple group) $\ZZ_2$.

Theorem: Jordan-Hölder theorem

Let $G$ be a finite group with $G\neq\qty{e}$. Then

1. $G$ has a composition series and
2. The composition factors in a composition series are unique, namely, if $\qty{e} = N_0\leq N_1\leq \cdots N_r = G$ and $\qty{e} = M_0 \leq M_1 \leq \cdots \leq M_s = G$ are two composition series for $G$, then $r=s$ and there is some permutation, $\pi$, of $\qty{1,2,\dots,r}$ such that

\[\begin{equation} M_{\pi(i)}/M_{\pi(i)-1} \cong N_i / N_{i-1}, \quad 1\leq i \leq r. \end{equation}\]

This motivates a two-part program for classifying all finite groups up to isomorphism:

The Hölder program

1. Classify all finite simple groups.
2. Find all ways of “putting simple groups together” to form other groups.

The classification of finite simple groups (part (1) of the Hölder program) is a monumental undertaking in algebra, completed by over a hundred mathematicians with tens of thousands of pages of text. This is beyond the scope of these notes; for more information, please refer to the Wikipedia.

5.4. Alternating groups

Note that for any $\sigma \in S_n$, there may be many ways of writing $\sigma$ as a product of transpositions. For fixed $\sigma$, the parity (i.e., an odd or even number of terms) is the same for any product of transpositions equaling $\sigma$.

Let $\epsilon(\sigma)$ be called the sign of $\sigma$. $\sigma$ is called an even permutation if $\epsilon(\sigma) = 1$ and an odd permutation if $\epsilon(\sigma)=-1$.

Proposition

The map $\epsilon:S_n \to \qty{\pm 1}$ is a homomorphism which means that $\epsilon(\sigma \tau) = \epsilon(\sigma) \epsilon(\tau)$.

Proposition

Transpositions are all odd permutations and $\epsilon$ is a surjective homomorphism.

Definition: alternating group

The alternating groups of degree $n$, denoted by $A_n$, is the kernel of the homomorphism (i.e., the ser of even permutations).

Note that $\abs{A_N} = \frac{1}{2}\abs{S_n} =\frac{n!}{2}$ and $A_n$ is a non-abelian simple group for all $n\geq 5$. The signs of permutation obey the usual $\ZZ_2$ laws:

\[\begin{align*} (\text{even})(\text{even}) &= (\text{odd})(\text{odd}) = \text{even},\\[.2cm] (\text{even})(\text{odd}) & = (\text{odd})(\text{even}) = \text{odd}. \end{align*}\]

Thus,

\[\begin{equation} \epsilon(\sigma) = \begin{cases} +1, \quad &\text{if $\sigma$ is a product of an even number of transpositions.}\\[.2cm] -1, &\text{if $\sigma$ is a product of an odd number of transpositions.} \end{cases} \end{equation}\]

So an $m$-cycle is an odd permutation if and only if $m$ is even. And $m$-cycle is an even permutation if and only if $m$ is odd.

Proposition

The permutation $\sigma$ is odd if and only if the number of cycles of even length in its cycle decomposition is odd.

Subgroup lattice of $A_4$.

TikZ code

\usepackage{mathtools, amsfonts,tikz-cd}
\newcommand{\lr}[1]{\langle#1\rangle}

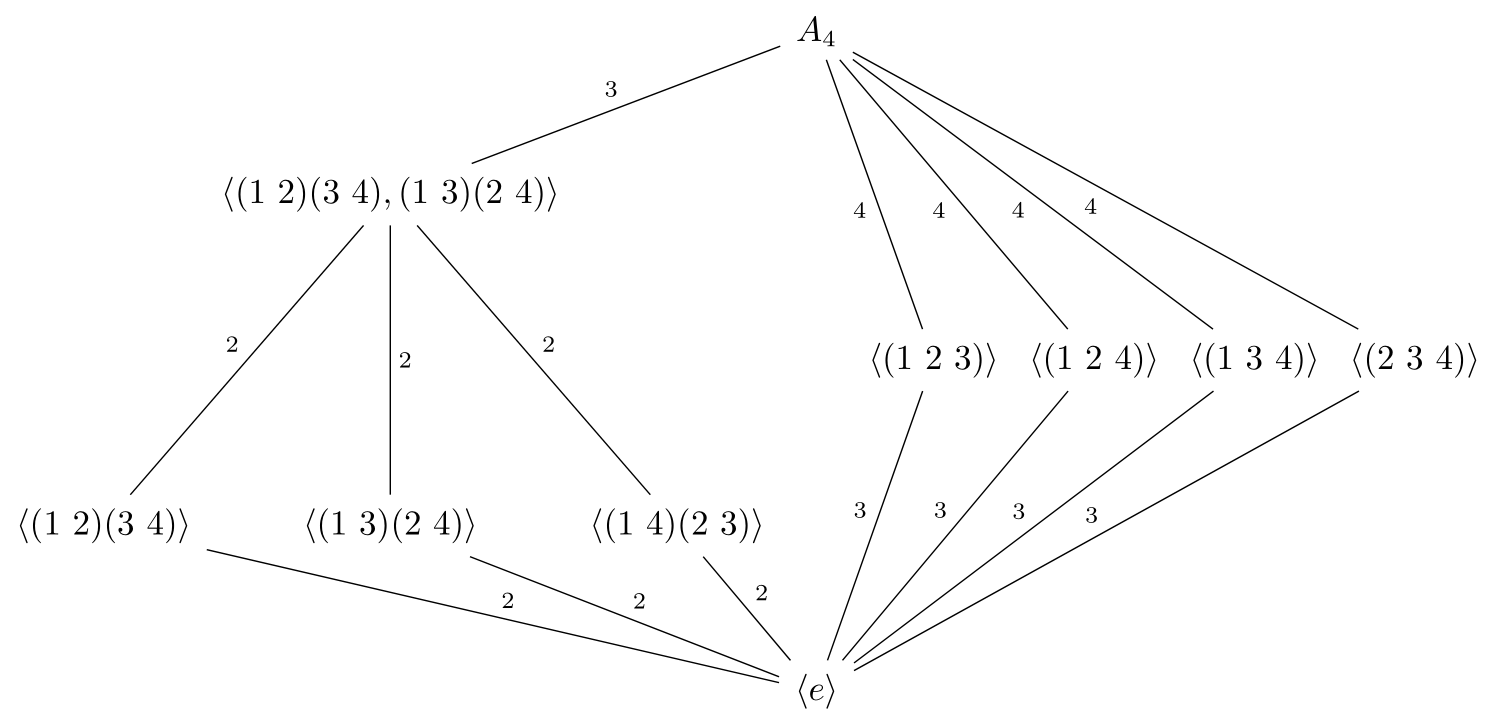
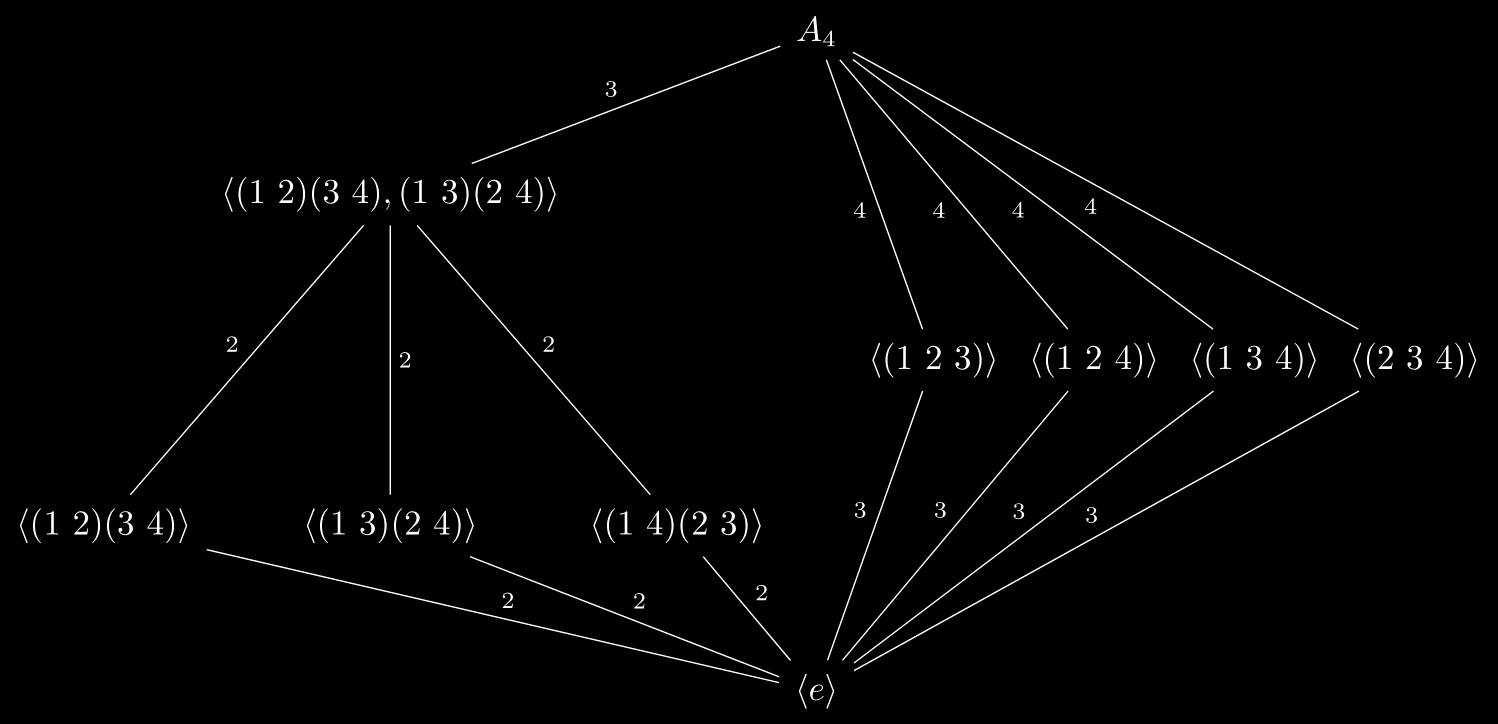
 \begin{tikzcd}[row sep =3em,column sep=0em,arrows=dash]
     &&& A_4 \ar[lld, "3"'] \ar[rdd,"4"']\ar[rrdd,"4"']\ar[rrrdd,"4"']\ar[rrrrdd,"4"']\\
     & \lr{(1\ 2)(3\ 4),(1\ 3)(2\ 4)} \ar[ldd,"2"']\ar[dd,"2"]\ar[rdd,"2"]\\
     &&&& \lr{(1\ 2 \ 3)}\ar[ldd,"3"'] & \lr{(1\ 2\ 4)}\ar[lldd,"3"'] & \lr{(1\ 3\ 4)}\ar[llldd,"3"'] & \lr{(2\ 3\ 4)}\ar[lllldd,"3"']\\
     \lr{(1\ 2)(3\ 4)}\ar[rrrd,"2"] & \lr{(1\ 3)(2\ 4)}\ar[rrd,"2"] & \lr{(1\ 4)(2\ 3)}\ar[rd,"2"]\\
     &&& \lr{e}
 \end{tikzcd}

6. Group actions

6.1. Definition of group action and permutation representation

Definition: group action

A group action of a group $G$ on a set $A$ is a map: $G\times A \to A$ (written as $g\cdot a$, $\forall g\in G$ and $\forall a\in A$) satisfying the following properties:

1. $g_1\cdot(g_2\cdot a) = (g_1g_2)\cdot a$, $\forall g_1,g_2\in G,a\in A$, and
2. $e\cdot a = a$, $\forall a\in A$.

Note that $\cdot$ is not a binary operation and $ga$ is always a member of $A$. In case where no danger of confusion, $g\cdot a$ will usually be written simply as $ga$.

This definition of an action is more precisely named a left action. We could similarly define a right action, i.e., $(a\cdot g_2)\cdot g_1 = a\cdot (g_2g_1)$.

Proposition

Let the group $G$ act on the set $A$. For each fixed $g\in G$ we get a map $\sigma_g$ defined by

\[\begin{equation} \sigma_{g}: A\to A ,\quad \sigma_{g}(a) = g\cdot a \end{equation}\]

then,

1. for each fixed $g\in G$, $\sigma_{g}$ is a permutation of $A$, and
2. the map from $G$ to $S_{A}$ defined by $g\mapsto \sigma_{g}$ is a homomorphism. The homomorphism from $G$ to $S_{A}$ is called the permutation representation associated to the given action.

Let $G$ be a group and $A\neq\emptyset$. Then, let $ga=a$, $\forall a\in G, a\in A$. This action is called the trivial action and $G$ is said to act trivially on $A$. The associated permutation representation $G\to S_{A}$ is the trivial homomorphism which maps every element of $G$ to the identity.

Examples: group action

• Let $G$ be any group and let $A=G$. Define a map from $G\times A$ to $A$ by $g\cdot a = ga$, $\forall g\in G,a\in A$. The two properties of group action is obviously true. This action is called the left regular action of $G$ on itself. Note that this action is faithful.
• Let $G$ be the group of $2\times 2$ matrices, \(\qty{\mqty(\cos\theta &\sin\theta\\-\sin\theta &\cos\theta)\bigg\vert \theta \in \RR}\), under matrix multiplication. Let $A = \RR^2$. When these matrices multiply a column vector $\vb{v}$, $\vb{v}$ will be rotated clockwise by $\theta$. It is easy to verify that this is a group action.

Definition: kernel, stabilzer, fithful

1. The kernel of the action is the set of elements of $G$ that act trivially on every element of $A:\qty{g\in G \ \vert \ g\cdot a = a, \forall a\in A}$.
2. For each $a\in A$ the stabilizer of $a$ in $G$ is the set of elements of $G$ that fix the element $a: \qty{g\in G\ \vert \ g\cdot a = a}$ and is denoted by $G_a$.
3. An action is faithful if its kernel is the identity.

Proposition

For any group $G$ and any nonempty set $A$ there is a bijection between the actions of $G$ on $A$ and the homomorphisms of $G$ into $S_{A}$.

Then the definition of a permutation representation may be rephrased.

Definition: permutation representation

If $G$ is a group, a permutation representation of $G$ is any homomorphism of $G$ into the symmetric group $S_{A}$ for some nonempty set $A$.

We shall say a given action of $G$ on $A$ affords or induces the associated permutation representation of $G$.

Proposition

Let $G$ be a group acting on the nonemtpy set $A$. The relation of $A$ defined by

\[\begin{equation} a\sim b \quad \text{if and only if $a=g\cdot b$ for some $g\in G$}. \end{equation}\]

is an equivalence relation. For each $a\in A$, the number of elements in the equivalence class containing $a$ is $\abs{G:G_{a}}$, the index of the stabilizer of $a$.

Definition: orbit

Let $G$ be a group acting on the nonempty set $A$.

1. The equivalence class $\qty{g\cdot a \ \vert \ g\in G}$ is called the orbit of $G$ containing $a$.
2. The action of $G$ on $A$ is called transitive if there is only one orbit.

Examples: orbit

• If $G$ acts trivially on $A$ then $G_a = G$ for all $a\in A$ an the orbits are all elements of $A$. This action is transitive if and only if $\abs{A} =1$.
• The group $D_4$ acts transitively on the set of two pairs of opposite vertices. In this action the stabilizer of any point is $\langle s,r^2 \rangle$ (which is of index $2$).

• Let $G$ be thepermutation group defined by

  \[G = \qty{(1),(1\ 2\ 3),(1\ 3\ 2),(4\ 5),(1\ 2\ 3)( 4\ 5),(1\ 3\ 2)(4\ 5)}\]

  acting on the set $A=\qty{1,2,3,4,5}$. The orbits are $\qty{1,2,3}$ and $\qty{4,5}$.

6.2. Cayley’s theorem

Theorem

Let $G$ be a group, let $H$ be a subgroup of $G$ and let $G$ act by left multiplication on the set $A$ of left cosets of $H$ in $G$. Let $\pi_{H}$ be the associated permutation representation afforded by this action. Then

1. $G$ acts transitively on $A$;
2. the stabilizer in $G$ of the point $e H \in A$ is the subgroup $H$;
3. the kernel of the action (i.e., the kernel of $\pi_H$) is $\displaystyle{\bigcap_{x\in G} xHx^{-1}}$ , and $\mathrm{ker}\ \pi_{H}$ is the largest normal subgroup of $G$ contained in $H$.

Proof

For (1), let $aH$ and $bH$ be any two elements of $A$, and let $g=ba^{-1}$. Then $g\cdot aH = (ba^{-1})aH = bH$, and so th two arbitrary elements $aH$ and $bH$ of $A$ lie in the same orbit.

For (2), the stabilzer of the point $e H$ is, bydefinition, $\qty{g\in G\ \vert \ g\cdot e H = eH}$, i.e., $\qty{g\in G \ \vert \ gH=H} = H$.

For (3), by definition of $\pi_H$ we have

\[\begin{align*} \mathrm{ker}\ \pi_H & = \qty{g\in G \ \vert \ gxH=xH, \forall x\in G}\\[.2cm] &=\qty{g\in G \ \vert \ (x^{-1}gx)H= H, \forall x\in G}\\[.2cm] &=\qty{g\in G \ \vert \ x^{-1}gx \in H, \forall x\in G}\\[.2cm] &=\qty{g\in G \ \vert \ g\in xHx^{-1}, \forall x\in G} = \bigcap_{x\in G} xHx^{-1}. \end{align*}\]

which proves the first assertion of (3). Then note that $\mathrm{ker}\ \pi_H\trianglelefteq G$ and $\mathrm{ker}\ \pi_H \trianglelefteq H$. If now $N$ is any normal subgroup of $G$ contained in $H$ then we have $N=xNx^{-1} \leq xHx^{-1}$ for all $x\in G$ so that

\[N \leq \bigcap_{x\in G}xHx^{-1} = \mathrm{ker}\ \pi_H.\]

This shows that $\mathrm{ker}\ \pi_H$ is the largest normal subgroup of $G$ contained in $H$.

∎

Theorem: Cayley's theorem

Every group is isomorphic to a subgroup of some symmetric group. If $G$ is a group of order $n$, then $G$ is isomorphic to a subgroup of $S_n$.

Cayley’s Theorem is what we call a representation theorem. The aim of representation theory is to find an isomorphism of some group $G$ that we wish to study into a group that we know a great deal about, such as a group of permutations or matrices.

It has the following corollary:

1. If $G$ is a finite group of order $n$ and $p$ is the smallest prime dividing $\abs{G}$, then any subgroup of index $p$ is normal.

6.3. The calss equation

Definition: conjugation

1. Two elements $a$ and $b$ of $G$ are said to be conjugate in $G$ if there is some $g\in G$ such that $b = gag^{-1}$. The orbits of $G$ acting on itself by conjugation are called the **conjugacy classes of ** $G$.
2. Two subsets $S$ and $T$ are said to be conjugate in $G$ if there is some $g\in G$ such that $T= gSg^{-1}$.

Proposition

The number of conjugates of a subset $S$ in a group $G$ is the index of the normalizer of $S$, $\abs{G:N_{G}(S)}$.

In particular, the number of conjugates of an element $s$ of $G$ is the index of the centralizer of $s$, $\abs{G:C_{G}(s)}$.

Theorem: the calss equation

Let $G$ be a finite group and let $g_1,g_2,\dots,g_r$ be representatives of the distinct conjugacy classes of $G$ not contained in the center $Z(G)$ of $G$. Then

\[\begin{equation} \abs{G} = \abs{Z(G)} + \sum_i^{r} \abs{G: C_{G}(g_i)}. \end{equation}\]

From the calss equation, we can get two important consequences:

1. If $p$ is a prime and $P$ is a group of prime power order $p^{\alpha}$ for some $\alpha \geq 1$, then $P$ has a nontrivial center: $Z(P)\neq \qty{e}$.
2. If $\abs{P} = p^2$ for some prime $p$, then $P$ is abelian. More precisely, $P$ is isomorphic to either $\ZZ_{p^2}$ or $\ZZ_p\times \ZZ_p$.

6.4. Automorphisms

Definition: automorphism

Let $G$ be a group. An isomorphism from $G$ onto itself is called an automorphism of $G$. The set of all automorphisms of $G$ is denoted by $\mathrm{Aut}(G)$.

$\mathrm{Aut}(G)$ is a group under composition of automorphisms, the automorphism group of $G$. And $\mathrm{Aut}(G)$ is a subgroup of $S_G$.

Proposition

Let $H$ be a normal subgroup of the group $G$. Then $G$ acts by conjugation on $H$ as automorphisms of $H$. More specifically, the action of $G$ on $H$ by conjugation is defined for each $g\in G$ by

\[\begin{equation} h\mapsto ghg^{-1}, \quad \text{for each $h\in H$}. \end{equation}\]

For each $g\in G$, conjugation by $g$ is an automorphism of $H$. The permutation representation afforded by this action is a homomorphism of $G$ into $\mathrm{Aut}(H)$ with kernel $C_{G}(H)$. In particular, $G/C_{G}(H)$ is isomorphic to a subgroup of $\mathrm{Aut}(H)$.

It has the following corollaries:

1. If $K$ is any subgroup of the group $G$ and $g\in G$, then $K \cong gKg^{-1}$. Conjugate elements and conjugate subgroups have the same order.
2. For any subgroup $H$ of a group $G$, the quotient group $N_{G}(H)/C_G(H)$ i isomorphic to a subgroup of $\mathrm{Aut}(H)$. In particular, $G/Z(G)$ is isomorphic to a subgroup of $\mathrm{Aut}(G)$.

Definition: inner automorphism

Let $G$ be a group and let $g\in G$. Conjugation by $g$ is called an inner automorphism of $G$ and the subgroup of $\mathrm{Aut}(G)$ consisting of all inner automorphisms is denoted by $\mathrm{Inn}(G)$.

Definition: characteristic subgroup

A subgroup $H$ of a group is called characteristic in $G$, denoted $H$ char $G$, if every automorphism of $G$ maps $H$ to itself, i.e., $\sigma(H)=H$ for all $\sigma \in \mathrm{Aut}(G)$.

For some specific groups, we have the following consequences:

• The automorphism group of the cyclic group of order $n$ is isomorphic to $(\ZZ/n\ZZ)^{\times}$, an abelian group of order $\varphi(n)$ (where $\varphi$ is Euler’s function).
• The automorphism group of the cyclic group of order $p^{n}$ where $p$ is an odd prime is cyclic of order $p^{n-1}(p-1)$.
• For all $n\neq 6$ we have $\mathrm{Aut}(S_n) = \mathrm{Inn}(S_n)\cong S_n$.
• $\mathrm{Aut}(D_4)\cong D_4$.
• $\mathrm{Aut}(Q_8)\cong S_4$.
• $\mathrm{Aut}(V_4)\cong GL_2(\mathbb{F}_2) \cong S_3$.

6.5. Sylow’s theorem

Definition: $p$-group

Let $G$ be a group and let $p$ be a prime.

1. A group of order $p^{\alpha}$ for some $\alpha\geq 1$ is called a $p$-group. Subgroups of $G$ which are $p$-groups are called $p$-subgroups.
2. If $G$ is a group of order $p^{\alpha}m$, where $p \nmid m$, then a subgroup of order $p^{\alpha}$ is called a Sylow $p$-subgroup of $G$.
3. The set of Sylow $p$-subgroups of $G$ will be denoted by $\mathrm{Syl}_{p}(G)$ and the number of Sylow $p$-subgroups of $G$ will be denoted by $n_p(G)$ (or just $n_p$ when $G$ is clear from the context).

Theorem: Sylow's theorem

Let $G$ be a group of order $p^{\alpha}m$, where $p$ is a prime number and $p\nmid m$.

1. Sylow $p$-subgroups of $G$ exist, i.e., $\mathrm{Syl}_p(G)\neq \emptyset$
2. If $P$ is a Sylow $p$-subgroup of $G$ and $Q$ is any $p$-subgroup of $G$, then there exists $g\in G$ such that $Q\leq g Pg^{-1}$, i.e., $Q$ is contained in some conjugate of $P$. In particular, any two Sylow $p$-subgroups of $G$ are conjugate in $G$.

3. The number of Sylow $p$-subgroups of $G$ is of the form $1+kp$, i.e.,

   \[\begin{equation} n_p \equiv 1 (\mathrm{mod} \ p). \end{equation}\]

   Further, $n_p$ is the index in $G$ of the normalizer $N_G(P)$ for any Sylow $p$-subgroup $P$, hence $n_p$ divides $m$.

From Sylow’s theorem, we can obtain the following corollaries: Let $P$ be a Sylow $p$-subgroup of $G$. Then the following are quivalent:

1. $P$ is the unique Sylow $p$-subgroup of $G$, i.e., $n_p=1$.
2. $P$ is normal in $G$.
3. $P$ is characteristic in $G$.
4. All subgroups generated by elements of $p$-power order are $p$-groups, i.e., if $X$ is any subset of $G$ such that $\abs{x}$ is a power of $p$ for all $x\in X$, then $\expval{X}$ is a $p$-group.

7. References

1. Dummit, D. S., and Foote, R. M. Abstract Algebra, 3rd ed. John Wiley & Sons, Inc. (2004).
2. Artin, M. Algebra, 2nd ed. Pearson Education. (2011).
3. Judson, T. M. Abstract Algebra: Theory and Application. Orthogonal Publishing L3c. (2022).