Affleck–Kennedy–Lieb–Tasaki Model

AKLT 模型（Affleck-Kennedy-Lieb-Tasaki 模型）作为量子自旋链中的一个重要模型，不仅在凝聚态物理中为拓扑量子相变的研究开辟了新路径，也为理解量子纠缠、拓扑序与边界效应提供了典型的理论范例。自 1980 年代以来，AKLT 模型在量子信息和量子计算等领域的理论研究中不断显示出其独特的价值，尤其是其基态的 Valence Bond Solid (VBS) 态，为未来拓扑量子态的物理实现提供了基本思路。

本文第一节介绍 AKLT 模型的相关背景，它和凝聚态物理中的 Haldane conjecture 有密切联系。第二节介绍了 Majumdar-Ghosh 模型，它和 AKLT 模型一样都可以被严格求解，它的基态被称为二聚体态（dimer state）。第三节具体介绍 AKLT 模型哈密顿量和基态的构造，第四节以隐性反铁磁序、矩阵乘积态、边缘态三个方面分析了 AKLT 模型的性质。

1. Haldane 猜想

我们从最简单的一维自旋链模型出发，也就是自旋-1/2 Heisenberg 模型，它的哈密顿量是

\[\begin{equation} H = J \sum_{i=1}^{N} \mathbf{S}_i \cdot \mathbf{S}_{i+1}, \label{Heisenberg-model} \end{equation}\]

这里我们只计及了最近邻格点间的相互作用，且考虑周期性边界条件，即 $\mathbf{S}_{N+1} = \mathbf{S}_{1}$。我们知道，当 $J<0$ 时，$\eqref{Heisenberg-model}$ 的基态为铁磁序；当 $J>0$ 时，$\eqref{Heisenberg-model}$ 的基态为反铁磁序，由 Hans Bethe 于 1931 年精确求解¹，相关资料可以查询 Bethe ansatz。在热力学极限下，反铁磁 Heisenberg 模型的能谱是无能隙的（gapless），系统的关联函数呈现幂律衰减。

我们现在只考虑 $J>0$ 时的反铁磁自旋 Heisenberg 模型。从上面的结果我们自然而然地有这样一个疑问，对于其他自旋量子数情况下的自旋链，它的能谱是否也是无能隙的？系统的关联函数是否也是幂次衰减的？

对于 $s=1/2$ 的情况可以精确求解，人们相信对于 $s\ge 1$ 的情况也不会有太大改变。但 Haldane 在 1983 年提出了一个猜想²（即 Haldane conjecture），对于反铁磁自旋 Heisenberg 模型：

• 当自旋 $s$ 是整数时，系统是有能隙的（gapped），关联函数呈指数衰减；
• 当自旋 $s$ 是半整数时，系统是无能隙的（gapless），关联函数呈幂律衰减。

这一猜想在当时凝聚态物理学界引起了很大的反响。从经典的角度来看，$s$ 仅仅是自旋的大小，为什么 $s$ 是整数还是半整数会引来如此大的差别？对于 $s=1$ 的情况很快就得到了数值（密度矩阵重整化群，DMRG）和实验（$\mathrm{CsNiCl_3}$）上的验证。

整数自旋系统的能隙不受微扰的影响，这个稳定存在的有能隙的量子态构成了一个非平庸的量子相（其基态没有对称性破缺，但因为存在边界态，而与平庸的有能隙的直积态有本质区别），后来被称为 Haldane phase，它也是一种对称性保护拓扑相³（symmetry protected topological phase, SPT phase）。

对于一般情况的自旋 Heisenberg 模型难以求解，Haldane conjecture 至今也没有得到纯数学意义上的证明，但从数值、场论、实验等多个角度都验证了它的正确性。

本文将要介绍的 AKLT 模型就是基于 $s=1$ 的反铁磁 Heisenberg 模型添加了一个修正项得来的，这种精心设计的哈密顿量的基态可以被严格求解，验证了 Haldane conjecture。虽然 AKLT 模型和 $s=1$ 的反铁磁 Heisenberg 模型并不完全一致，但它们的基态都属于 Haldane phase，具有共同的性质，我们会发现，在 AKLT 模型自旋链的边缘会出现自旋-1/2 自由度，它们并不与主体链形成配对态，从而形成了一种非局域的拓扑特性。这一现象也说明 AKLT 模型具有边缘态和拓扑保护的特性。

2. Majumdar-Ghosh 模型

推广自旋-1/2 Heisenberg 模型的一个自然想法就是引入次近邻相互作用，也即 $J_1$-$J_2$ 模型，

\[\begin{equation} H = J_1 \sum_{i=1}^{N} \mathbf{S}_i \cdot \mathbf{S}_{i+1} + J_2 \sum_{i=1}^{N} \mathbf{S}_i\cdot \mathbf{S}_{i+2}. \end{equation}\]

次近邻相互作用实际上会引入阻挫（frustration），这就是另外的故事了。我们考虑一个特殊情况，即 $J_1= 2 J_2 =J$，这就是 Majumdar-Ghosh 模型⁴，

\[\begin{equation} H_{\mathrm{MG}} = \sum_{i=1}^{2N}\left(\mathbf{S}_i \cdot \mathbf{S}_{i+1} + \frac{1}{2} \mathbf{S}_{i}\cdot \mathbf{S}_{i+2}\right), \label{Majumdar-Ghosh-model} \end{equation}\]

其中 $s_i=1/2$，且引入了周期性边界条件，自旋链的长度为偶数 $2N$。为简便起见，已经令上式中的 $J=1$。当然我们也可以进一步把 Majumdar-Ghosh 模型的哈密顿量改写为：

\[\begin{align*} H_{\mathrm{MG}} = \frac{1}{2}\sum_{i=1}^{2N}\qty(\mathbf{S}_i\cdot \mathbf{S}_{i+1} + \mathbf{S}_{i+1}\cdot \mathbf{S}_{i+2} + \mathbf{S}_{i}\cdot \mathbf{S}_{i+2})= \frac{1}{4}\sum_{i=1}^{2N}\qty[\qty(\mathbf{S}_i+\mathbf{S}_{i+1} + \mathbf{S}_{i+2})^2 - \frac{9}{4}], \end{align*}\]

其中括号里的正是 site $i$, $i+1$, $i+2$ 处三个自旋耦合后投影到总自旋 $s=3/2$ 子空间的投影算符。我们知道三个自旋-1/2 粒子耦合后的总自旋可以是 $s=1/2$, $3/2$，如果我们能设法使得每一组三个粒子耦合后的总自旋为 1/2，那我们就找到了系统能量的最低态（也就是基态）。

这种构造显然是可以的，我们以前三个粒子为例，若它们的态矢量可以写为：

\[\begin{equation*} \ket{\phi_{123}} = (\ket{\uparrow_1\downarrow_2}-\ket{\downarrow_1\uparrow_2})\otimes\ket{\uparrow_3}, \end{equation*}\]

由于前两个粒子耦合成了自旋单态，所以三个粒子组成的整体总自旋是 $1/2$。我们把这种构造不断复制，就可以得到 Majumdar-Ghosh 模型的一个基态（补上了归一化系数）：

\[\begin{align} \ket{\Phi_{\mathrm{MG}}^{(1)}} &= \frac{\ket{\uparrow\downarrow}-\ket{\downarrow\uparrow}}{\sqrt{2}} \cdots\frac{\ket{\uparrow\downarrow}-\ket{\downarrow\uparrow}}{\sqrt{2}} = \bigotimes_{i=1}^{N} \frac{1}{\sqrt{2}}\qty(\ket{\uparrow_{2i-1}\downarrow_{2i}} - \ket{\downarrow_{2i-1}\uparrow_{2i}}). \end{align}\]

由于系统具有平移不变性，我们把上述基态中的每个自旋都翻过来（相当于整体平移了一个位置），它仍然是系统的基态，也即

\[\begin{align} \ket{\Phi_{\mathrm{MG}}^{(2)}} = \bigotimes_{i=1}^{N} \frac{1}{\sqrt{2}}\qty(\ket{\uparrow_{2i}\downarrow_{2i+1}} - \ket{\downarrow_{2i}\uparrow_{2i+1}}). \end{align}\]

可以证明 Majumdar-Ghosh 模型的基态是二重简并的⁵，我们找到的这两个态就是系统线性独立的两个基态。我们可以用图像来形象地描述这两个基态 $\vert\Phi_{\mathrm{MG}}^{(1)}\rangle$, $\vert\Phi_{\mathrm{MG}}^{(2)}\rangle$，

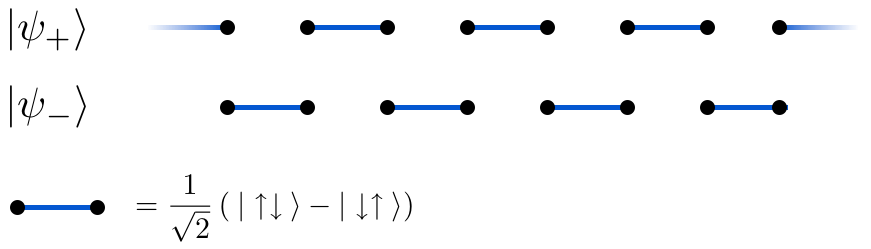Majumdar-Ghosh 模型的基态，其中 $\ket{\psi_+}$, $\ket{\psi_-}$ 就是 $\vert\Phi_{\mathrm{MG}}^{(1)}\rangle$, $\vert\Phi_{\mathrm{MG}}^{(2)}\rangle$，图源 Milez。

其中每一条线段都代表连接相邻 site 自旋-1/2 粒子构成的自旋单态，这其实就有点类似于化学里的化学键，每个自旋单态被称为 valence bond，显然 Majumdar-Ghosh 模型里不同的 valence bond 之间没有关联，系统基态仅仅是不同 valence bond 的直积。

如果将其中一组自旋单态变为自旋三重态，我们就得到了 Majumdar-Ghosh 模型的第一激发态，显然它和基态之间存在着一个非零的能隙。注意这一点并不违反 Lieb-Schultz-Mattis 定理，因为 Majumdar-Ghosh 模型的基态是二重简并的。

Ground states of the Majumdar-Ghosh model

Majumdar-Ghosh 模型二重简并的基态是（周期性边界条件）：

\[\begin{align*} \ket{\Phi_{\mathrm{MG}}^{(1)}}& =\bigotimes_{i=1}^{N} \frac{1}{\sqrt{2}}\qty(\ket{\uparrow_{2i-1}\downarrow_{2i}} - \ket{\downarrow_{2i-1}\uparrow_{2i}}), \\[.2cm] \ket{\Phi_{\mathrm{MG}}^{(2)}} &= \bigotimes_{i=1}^{N} \frac{1}{\sqrt{2}}\qty(\ket{\uparrow_{2i}\downarrow_{2i+1}} - \ket{\downarrow_{2i}\uparrow_{2i+1}}). \end{align*}\]

并且注意到 $\braket*{\phi_{\mathrm{MG}}^{(1)}}{\phi_{MG}^{(2)}} = 2(-1/2)^N$，如果自旋链长度 $2N\to\infty$，那么这两个基态就是正交的。

3. AKLT 模型

受到 Majumdar-Ghosh 模型的启发，如果我们希望找到由自旋单态组成的量子态作为系统基态的哈密顿量，一种简单而有效的方法是将哈密顿量表示为一串投影算符的组合，这些投影算符的作用是将量子态投影到与自旋单态正交的子空间中，因此，系统的基态能量为零，因为投影后的部分与自旋单态正交，最小能量对应着基态。

我们可以把这种套路用到更高自旋量子数的情况，在 1987 年， Affleck, Kennedy, Lieb 和 Tasaki 就提出了 AKLT 模型⁶，

\[\begin{equation} H_{\mathrm{AKLT}} = \sum_{i=1}^{N}\qty[ \mathbf{S}_i\cdot\mathbf{S}_{i+1} + \frac{1}{3} \left(\mathbf{S}_i\cdot\mathbf{S}_{i+1}\right)^2]. \label{AKLT-model} \end{equation}\]

其中 $s_i = 1$，且考虑了周期性边界条件，而这其实就是两个自旋-1 粒子耦合后投影到总自旋 $s=2$ 子空间的投影算符。注意 $\eqref{AKLT-model}$ 有着丰富的对称性，除了时间反演对称性（$\mathbf{S}\to - \mathbf{S}$）之外，还有 $\mathrm{SU}(2)$ 对称性。

从左至右分别是 Ian Affleck, Tom Kennedy, Elliott H. Lieb, 和 Hal Tasaki，令人遗憾的是 Ian Affleck 已于本月初离世。

在这里我们做一个简短的说明。考虑两个自旋-1 粒子耦合后的投影算符 $P_0$, $P_1$, $P_2$，分别代表投影到总自旋 $s=0,1,2$ 的子空间，而总自旋算符的平方 $\mathbf{S}^2 = (\mathbf{S}_i+\mathbf{S}_{i+1})^2$（其实就是 Casimir 算符）和投影算符是对易的，它们有共同的本征态 $\ket{s=0,m}$,$\ket{s=1,m}$, $\ket{s=2,m}$，我们可以依此列一个本征值表格：

\[\begin{array}{c||c} \ket{s,m} & \mathbf{S}^2 & P_0 & P_1 &P_2\\[.2cm] \hline s=0 & 0 & 1 & 0 & 0 \\[.2cm] \hline s=1 & 2 & 0 & 1 & 0 \\[.2cm] \hline s=2 & 6 &0 &0 & 1 \end{array}\]

依据这个表格，我们就可以直接写出投影算符的表达式：

\[\begin{align} P_0 &= \frac{1}{12}(\mathbf{S}^2 -2)(\mathbf{S}^2 -6) = \frac{1}{3}(\mathbf{S}_i\cdot\mathbf{S}_{i+1})^2 - \frac{1}{3},\\[.2cm] P_1 &= -\frac{1}{8} \mathbf{S}^2(\mathbf{S}^2-6) = -\frac{1}{2} (\mathbf{S}_i\cdot\mathbf{S}_{i+1})^2 - \frac{1}{2}\mathbf{S}_i\cdot\mathbf{S}_{i+1} + 1,\\[.2cm] P_2 & = \frac{1}{24}\mathbf{S}^2(\mathbf{S}^2-2) = \frac{1}{6}(\mathbf{S}_i\cdot\mathbf{S}_{i+1})^2 + \frac{1}{2} \mathbf{S}_i\cdot\mathbf{S}_{i+1} + \frac{1}{3}. \label{projector of AKLT} \end{align}\]

显然 $\eqref{projector of AKLT}$ 正是 AKLT 模型中哈密顿量的局域项（改变了比例系数，并求丢掉了常数项），如果系统中每对耦合的两个自旋组成 $s=0$ 或者 $s=1$ 的态，那么整个系统就处于能量最低的态，也即基态。关于这部分内容的解释，也可以参考 AKLT 模型的哈密顿量是怎么得出的。

这种方法和传统凝聚态的套路是反过来的，一般我们是先写下一个模型的哈密顿量，然后进行一通暴算得到模型的各种性质，比如基态、激发态、关联函数等。但在这里我们其实是先确定一个特定的态， 再基于这个态构造以它为基态的 parent Hamiltonian。

出于以上想法，我们可以将每个 site 的自旋-1 粒子视作两个自旋-1/2 粒子耦合成的自旋三重态，再令相邻 site 的自旋-1/2 粒子耦合成自旋单态。这样任意两个相邻 site 的两个自旋-1 粒子（或者说四个自旋-1/2 粒子）耦合后 的总自旋是 $s=0,1$，我们便得到了 AKLT 模型的基态，

\[\begin{equation} \ket{\Phi_{\mathrm{AKLT}}} = \bigotimes_{j=1}^{N} \mathcal{P}_j \bigotimes_{i=1}^{N}\frac{1}{\sqrt{2}}(\ket{\uparrow_{i}^{r}\downarrow_{i+1}^{l}} - \ket{\downarrow_{i}^{r}\uparrow_{i+1}^{l}}). \label{AKLT-gs} \end{equation}\]

其中 $\mathcal{P}_j = \ket{1} \bra{\uparrow_{j}^{l}\uparrow_j^{r}} +\ket{0}\qty(\bra{\uparrow_{j}^{l}\downarrow_{j}^{r}} +\bra{\downarrow_{j}^{l}\uparrow_{j}^{r}})/\sqrt{2} + \ket{-1}\bra{\downarrow_{j}^{l}\downarrow_{j}^{r}}$ 表示同一个 site 的两个自旋-1/2 粒子投影到 $s=1$ 自旋三重态的投影算符。AKLT 模型的基态被称为 VBS (valence-bond solid) state，其中一组自旋单态也被称为 valence bond，通过投影算符 $\mathcal{P}_j$ 把相邻的 valence bond 耦合到了一起，这一点与 Majumdar-Ghosh 模型是不同的。

如下图所示：

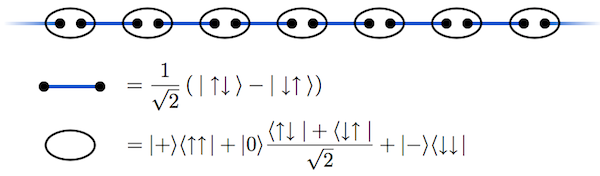AKLT 模型的基态，每个 site 处的自旋-1 粒子可以分解为两个自旋-1/2 粒子耦合成的自旋三重态。相邻 site 的自旋-1/2 粒子耦合成自旋单态，用线段表示。图中的圆圈代表两个自旋-1/2 粒子投影到 $s=1$ 的投影算符。图源 Milez。

可以证明⁷，在周期性边界条件下，AKLT 模型的基态是唯一的，系统的激发态和基态之间有非零的能隙 $\Delta E_0$，基态的关联函数满足：

\[\begin{equation} \lim_{N\to\infty} \frac{\expval{\mathbf{S}_i\cdot\mathbf{S}_j}{\Phi_{\mathrm{AKLT}}}}{\braket{\Phi_{\mathrm{AKLT}}}} = 4 (-3)^{-|i-j|} = 4(-1)^{i-j} \mathrm{e}^{-|i-j|/\xi}, \label{correlation-function} \end{equation}\]

其中关联长度 $\xi = 1/\ln 3 \simeq 0.91$，符合 Haldane conjecture 的指数衰减。Knabe 在 1988 年证明了能隙的下界 $\Delta E_0 \geq 0.496$，与自旋链的长度无关⁸。

另外，在不破坏 $\mathrm{SU}(2)$ 对称性和时间反演对称性的条件下，我们对系统施加一个小扰动，基态总是唯一的，且激发态和基态之间依然有非零的能隙⁹。这说明系统的能隙和基态唯一性不受微扰的影响，它其实就是一种 Haldane phase。

Unique ground state of the AKLT model

AKLT 模型唯一的基态是（周期性边界条件）：

\[\begin{equation*} \ket{\Phi_{\mathrm{AKLT}}} = \bigotimes_{j=1}^{N} \mathcal{P}_j \bigotimes_{i=1}^{N}\frac{1}{\sqrt{2}}(\ket{\uparrow_{i}^{r}\downarrow_{i+1}^{l}} - \ket{\downarrow_{i}^{r}\uparrow_{i+1}^{l}}). \end{equation*}\]

其中 $\mathcal{P}_j = \ket{1} \bra{\uparrow_{j}^{l}\uparrow_j^{r}} +\ket{0}\qty(\bra{\uparrow_{j}^{l}\downarrow_{j}^{r}} +\bra{\downarrow_{j}^{l}\uparrow_{j}^{r}})/\sqrt{2} + \ket{-1}\bra{\downarrow_{j}^{l}\downarrow_{j}^{r}}$。

4. AKLT 模型的性质

AKLT 模型除了提供 Haldane conjecture 的一个严格可解实例之外，还蕴藏了非常多的奇妙性质，我们这里具体探讨其中几个¹⁰。

4.1. 隐性反铁磁序

在经典的反铁磁材料中，反铁磁序的特点是相邻的自旋（例如自旋-1/2）朝向相反，形成交替排列的 Néel 序。例如，一个简单的自旋-1/2 反铁磁链可以表示为：

\[\begin{equation*} \cdots \uparrow\downarrow\uparrow\downarrow \cdots \end{equation*}\]

隐性反铁磁序并不像上面传统的反铁磁序那样可以通过直接观察自旋的空间排列来发现。在 AKLT 模型中，我们从基态 $\eqref{AKLT-gs}$ 中没有直接看到自旋“朝上和朝下交替排列”，但它其实仍然表现出反铁磁性，我们称它为隐性反铁磁序（hidden antiferromagnetic order）。

我们可以这样分析，考虑 site $i$ 和 $i+1$ 处的 valence bond，并对其标记 $\alpha_{i+1}=1,2$。如果 valence bond 处于 $\ket{\uparrow_{i}^{r}\downarrow_{i+1}^{l}}/\sqrt{2}$，那我们就标记 $\alpha_{i+1}=1$；如果 valence bond 处于 $\ket{\downarrow_{i}^{r}\uparrow_{i+1}^{l}}/\sqrt{2}$，我们就标记 $\alpha_{i+1} =2$。如下图所示，具体展示了 $\eqref{AKLT-gs}$ 中展开后的其中一项。

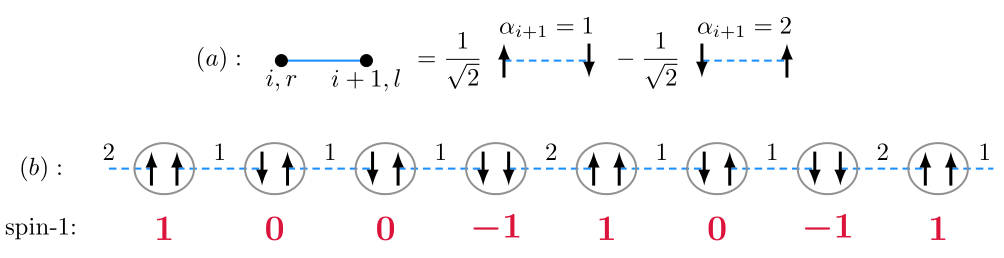(a) 一个 valence bond 对应一个自旋单态，我们将 $\ket{\uparrow_{i}^{r}\downarrow_{i+1}^{l}}/\sqrt{2}$, $\ket{\downarrow_{i}^{r}\uparrow_{i+1}^{l}}/\sqrt{2}$ 分别用 $\alpha_{i+1}=1,2$ 来进行区分。 (b) AKLT 模型基态展开后是特定自旋配置的组合，这里展示的是其中一项。

如果我们把 $s=0$ 全部删去，显然我们剩下的就是 $s=1,s=-1$ 交替排列的自旋链，它显然是一个反铁磁序。

注意：上述交替排列的 $1,-1$ 并不意味着基态有长程反铁磁序，这是因为在自旋链中还随机穿插着 $s=0$，因此并不违反 Haldane conjecture。

对于一般情况，我们也可以从延长自旋链的角度一步步考虑。假设 site 1 处的自旋是 $\cdots\uparrow\uparrow\cdots$，它对应的是 $s_1=1$。为了保证 bond 的总自旋为 0，则下一个连接的就必须是 $\downarrow$，也即 $\cdots\uparrow\uparrow\cdots\downarrow?$。这里的 $?$ 表示待定：

• 它可以取 $\uparrow$，那么 site 2 处就对应 $s_2=0$，即 $\cdots\uparrow\uparrow\cdots\downarrow\uparrow\cdots\downarrow?$;
• 也可以取 $\downarrow$，那么 site 2 处就对应 $s_2=-1$，即 $\cdots\uparrow\uparrow\cdots\downarrow\downarrow\cdots\uparrow?$。

依次不断连接下去，我们就会发现 $1,-1$ 必定是交错出现的，必不可能出现 $1,1$ 或 $-1,-1$ 的结构，比如 $\cdots\uparrow\uparrow\cdots\uparrow\uparrow\cdots$ 显然是不允许的，因为 bond 的总自旋必须是 $0$。

值得一提的是，尽管 AKLT 模型的基态是 VBS 态，通过 valence bond 进行连接，看起来就像是固体一样，但从我们上面的讨论来说并非如此，它更像是某种液体，每个 site 处的 $s=1,-1$ 并不固定，并且自旋链中可以随意穿插 $s=0$。这正是量子液体的一个典型特征，即系统的局部态不是固定不动的，而是充满了量子涨落。因此，VBS 态也可以被看作是带有隐性反铁磁序的量子自旋液体。

4.2. 矩阵乘积表示

张量网络是一类用于处理量子多体系统复杂问题的强有力工具，最近一二十年在凝聚态物理和量子信息领域取得了显著的进展¹¹。它的核心思想是通过将一个高阶量子态分解为多个低阶张量的缩并形式，从而将量子态的全局表示转化为局部张量的网络表示，显著减少所需的参数量，巧妙规避了高纠缠态的指数增长问题，同时保持了对态的高精度近似。

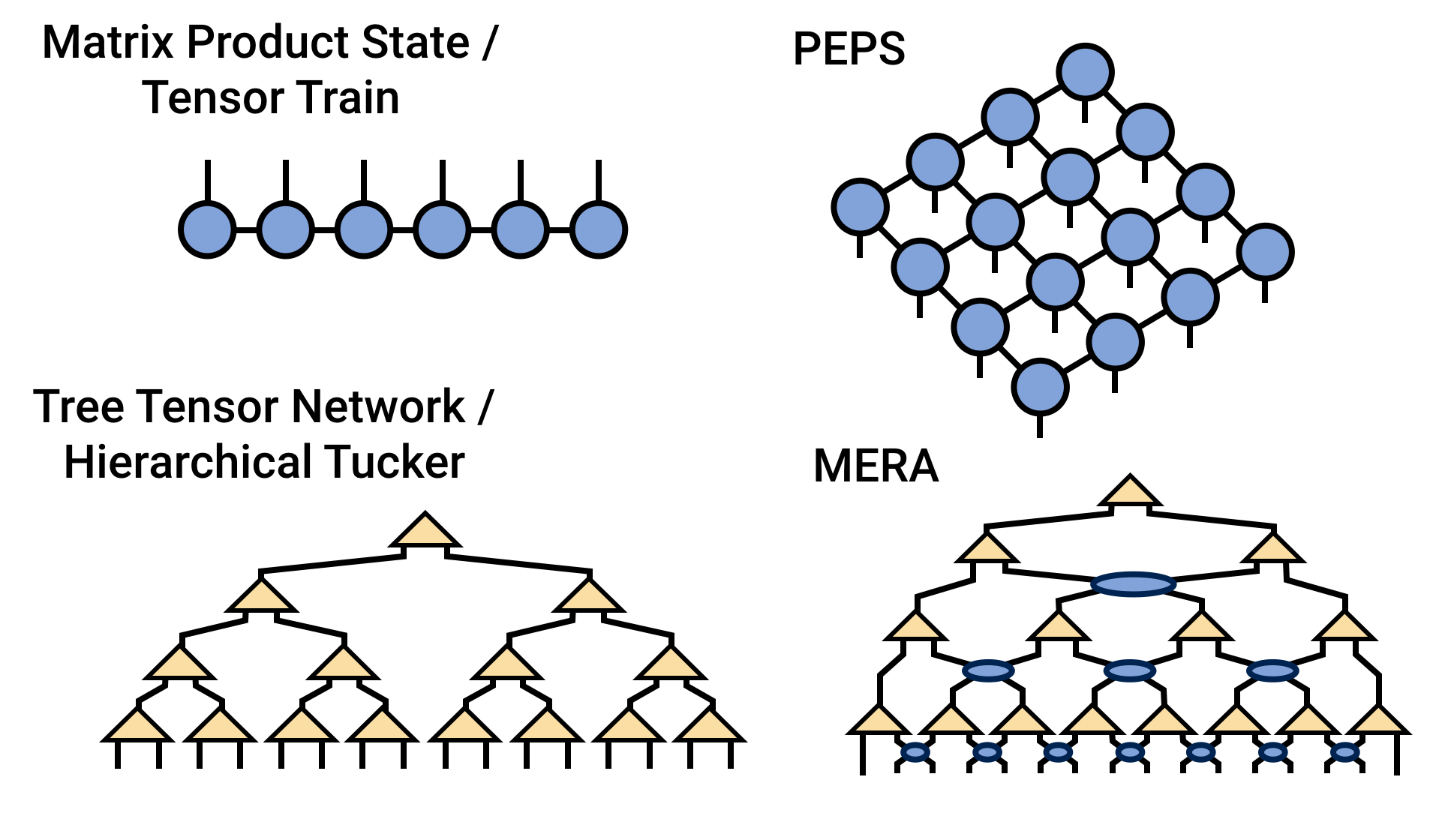几类常见的张量网络，分别是矩阵乘积态（MPS）、投影纠缠对态（PEPS）、树状张量网络（TTN）、多尺度纠缠重整化（MERA），图源 Tensor Network

而矩阵乘积态（matrix product state, MPS）是最常见的张量网络，尤其适用于刻画一维量子多体系统，比如描述自旋链的基态和低能激发态等。另外 MPS 最成功的例子就是密度矩阵重整化群方法（Density Matrix Renormalization Group, DMRG），它是一维情况里非常精准的数值算法。

我们可以先考虑一个更一般的自旋链，如下图所示：

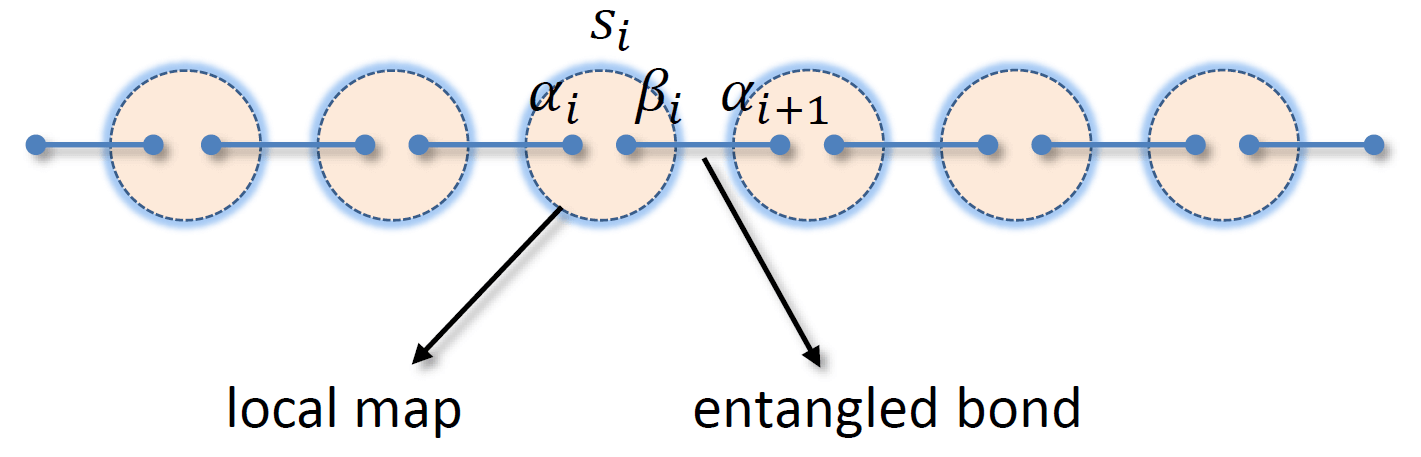更一般的自旋链，每个 site 处的自旋用 $s_i$ 来表示，它可以被看作是两个自旋 $\alpha_i,\beta_i$ 耦合后投影得到的，相邻 site 的自旋形成 entangled bond。图源 Honghao Tu’s Lectures。

我们把每个 site 上的物理自由度用 $s_i$ 来表示，它被分解为两个虚拟自由度 $\alpha_i,\beta_i$，经过投影算符 $\mathcal{P}_i$ 可以回到物理自由度上，其中

\[\begin{equation} \mathcal{P}_i = \sum_{s_i=1}^{d}\sum_{\alpha_i,\beta_i=1}^{D} B_{\alpha_i\beta_i}^{s_i}\ket{s_i}\bra{\alpha_i,\beta_i}, \end{equation}\]

其中 $B_{\alpha_i\beta_i}^{s_i}$ 是展开系数，而 entangled bond 可以表示成：

\[\begin{equation} \ket{I}_{i,i+1} = \sum_{\beta_i,\alpha_{i+1}=1}^{D} R_{\beta_i\alpha_{i+1}}\ket{\beta_i,\alpha_{i+1}}, \end{equation}\]

这里的 $R_{\beta_i,\alpha_{i+1}}$ 也表示展开系数。那么上图表示的态矢量可以写成：

\[\begin{equation} \ket{\psi_{\mathrm{PBC}}} = \Big(\bigotimes_{j=1}^{N} \mathcal{P_j}\Big)\Big(\bigotimes_{i=1}^{N}\ket{I}_{i,i+1}\Big). \end{equation}\]

经过一些并不复杂的运算，我们可以得到：

\[\begin{align*} \ket{\psi_{\mathrm{PBC}}} &= \Big(\bigotimes_{j=1}^{N} \mathcal{P_j}\Big)\Big(\bigotimes_{i=1}^{N}\ket{I}_{i,i+1}\Big)\\[.2cm] & = \sum_{s_1,\dots, s_N=1}^{d} \sum_{\alpha_1,\beta_1,\dots,\alpha_{N},\beta_{N}=1}^{D} \qty(B_{\alpha_1\beta_1}^{s_1}\cdots B_{\alpha_{N}\beta_N}^{s_N}) \ket{s_1,\dots, s_N} \bra{\alpha_1,\beta_1,\dots,\alpha_N,\beta_N}\\[.2cm] &\qquad \times \sum_{\alpha_1',\beta_1',\dots,\alpha_{N}',\beta_{N}'=1}^{D}\qty(R_{\beta_1'\alpha_2'}\cdots R_{\beta_N'\alpha_1'}) \ket{\alpha_1',\beta_1',\dots,\alpha_N',\beta_N'}\\[.2cm] &=\sum_{s_1,s_N=1}^{d} \sum_{\alpha_1,\beta_1,\dots,\alpha_N,\beta_N=1}^{D}\qty(B_{\alpha_1\beta_1}^{s_1}R_{\beta_1\alpha_2}\cdots B_{\alpha_N\beta_N}^{s_N} R_{\beta_N\alpha_1}) \ket{s_1,\dots,s_N}\\[.2cm] &=\sum_{s_1,s_N=1}^{d} \mathrm{Tr}(B^{s_1}R\cdots B^{s_2}R)\ket{s_1,\dots,s_N}. \end{align*}\]

我们可以定义 $A^{s_i}:= B^{s_i}R$，可以将上式简化为：

\[\begin{equation} \ket{\psi_{\mathrm{PBC}}} = \sum_{s_1,\dots,s_N=1}^{d} \mathrm{Tr}(A^{s_1} A^{s_2}\cdots A^{s_N})\ket{s_1,s_2,\dots,s_N}. \label{PBC} \end{equation}\]

如果我们考虑的是开边界条件，那么同理也可以得到：

\[\begin{equation} \ket{\psi_{\mathrm{OBC}}(\alpha_1\beta_N)} = \sum_{s_1,\dots,s_N=1}^{d} (A^{s_1} A^{s_2}\cdots \tilde{A}^{s_N})_{\alpha_1\beta_N}\ket{s_1,s_2,\dots,s_N}, \quad \text{where $\tilde{A}^{s_N} = B^{s_N}$} \label{OBC} \end{equation}\]

我们可以对每个矩阵 $A$ 用图像的形式表示，水平伸出去的两条腿代表 virtual freedom，竖直向上的一条腿代表 physical freedom。不同 $A$ 连接的两条腿代表缩并。那么我们可以将量子态 $\ket{\psi}$ 用图像的形式表示：

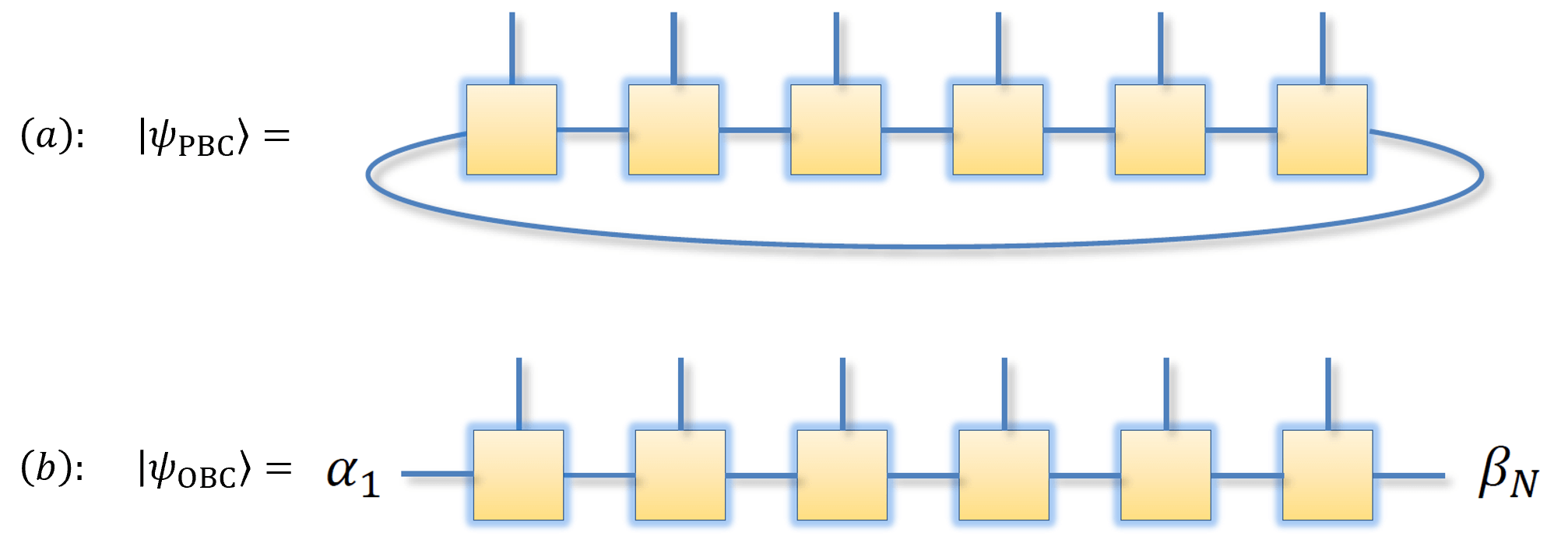MPS 示意图：(a) 代表周期性边界条件。(b) 代表开边界条件。图源 Honghao Tu’s Lectures。

从上面的分析中我们可以看出来 AKLT 模型的基态 $\eqref{AKLT-gs}$ 是一个典型的 MPS，其中

\[\begin{align*} \mathcal{P}_i &= \ket{1} \bra{\uparrow_{i}^{l}\uparrow_i^{r}} +\ket{0}\frac{\bra{\uparrow_{i}^{l}\downarrow_{i}^{r}} +\bra{\downarrow_{i}^{l}\uparrow_{i}^{r}}}{\sqrt{2}} + \ket{-1}\bra{\downarrow_{i}^{l}\downarrow_{i}^{r}},\\[.2cm] \ket{I}_{i,i+1} &= \frac{1}{\sqrt{2}}\qty(\ket{\uparrow_{i}^{r}\downarrow_{i+1}^{l}} - \ket{\downarrow_{i}^{r}\uparrow_{i+1}^{l}}). \end{align*}\]

于是

\[\begin{equation*} R = \frac{1}{\sqrt{2}}\begin{pmatrix} 0 & 1 \\ -1 &0 \end{pmatrix}, \quad B^{s=1} = \begin{pmatrix} 1& 0 \\ 0 &0 \end{pmatrix}, \quad B^{s=0} = \frac{1}{\sqrt{2}}\begin{pmatrix} 0&1 \\ 1&0 \end{pmatrix},\quad B^{s=-1}= \begin{pmatrix} 0& 0 \\ 0& 1 \end{pmatrix}. \end{equation*}\]

由此得到

\[\begin{equation} A^{s=1} = \frac{1}{\sqrt{2}}\begin{pmatrix} 0 & 1 \\ 0 &0 \end{pmatrix}, \quad A^{s=0} = \frac{1}{2} \begin{pmatrix} -1&0\\ 0&1 \end{pmatrix},\quad A^{s=-1} = \frac{1}{\sqrt{2}}\begin{pmatrix} 0& 0 \\ -1 &0 \end{pmatrix}. \end{equation}\]

AKLT 模型的基态 $\eqref{AKLT-gs}$ 就可以表示成：

\[\begin{equation} \begin{split} \ket{\Phi_{\mathrm{AKLT}}} &= \sum_{s_1,\dots,s_N} \mathrm{Tr}(A^{s_1}A^{s_2} \cdots A^{s_N}) \ket{s_1,s_2,\dots,s_N}\\[.2cm] & = \mathrm{Tr}(g_1g_2\cdots g_N). \end{split} \end{equation}\]

其中

\[\begin{equation} g_i = \sum_{s_i=-1,0,1} A^{s_i}\ket{s_i} = \frac{1}{\sqrt{2}} \begin{pmatrix} -\ket{0}_i & \sqrt{2}\ket{1}_i \\ -\sqrt{2}\ket{-1}_i & \ket{0}_i \end{pmatrix}. \end{equation}\]

利用 MPS 表示，我们也可以方便地计算出基态 $\eqref{AKLT-gs}$ 的归一化系数以及关联函数，如下图所示

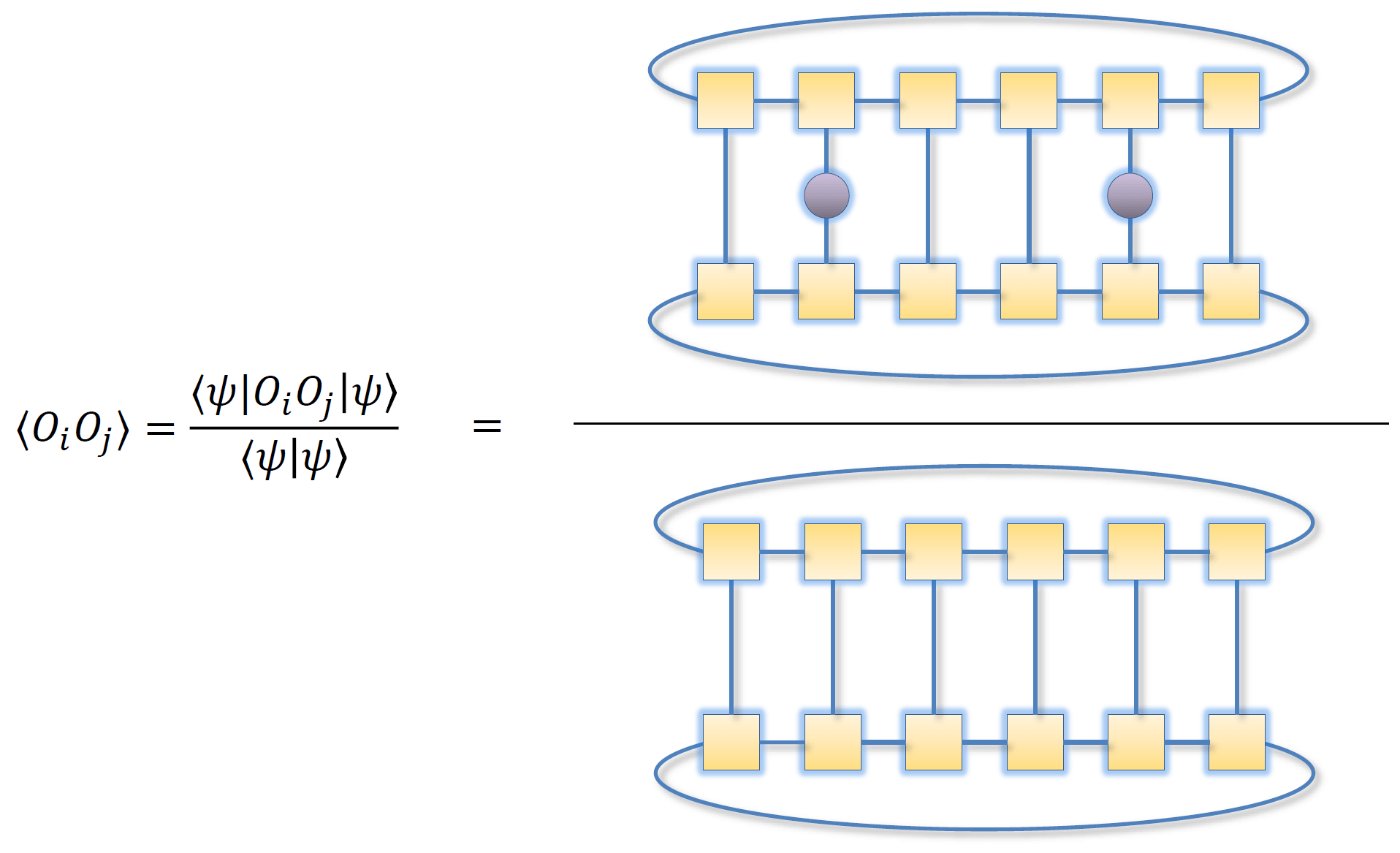利用 MPS 表示计算关联函数，图源 Honghao Tu’s Lectures。

通过一些计算就可以得到¹⁰：

\[\begin{equation} \lim_{N\to\infty} \frac{\expval{\mathbf{S}_{i}\cdot\mathbf{S}_{i+r}}{\Phi_{\mathrm{AKLT}}}}{\braket{\Phi_{\mathrm{AKLT}}}} = 4 \qty(-\frac{1}{3})^{r}, \end{equation}\]

这与之前提到的 $\eqref{correlation-function}$ 是一致的。

MPS representation of the AKLT model

AKLT 模型的基态可以用 MPS 表示：

\[\begin{equation*} \begin{split} \ket{\Phi_{\mathrm{AKLT}}} &= \sum_{s_1,\dots,s_N} \mathrm{Tr}(A^{s_1}A^{s_2} \cdots A^{s_N}) \ket{s_1,s_2,\dots,s_N}\\[.2cm] & = \mathrm{Tr}(g_1g_2\cdots g_N). \end{split} \end{equation*}\]

其中

\[\begin{gather*} A^{s=1} = \frac{1}{\sqrt{2}}\begin{pmatrix} 0 & 1 \\ 0 &0 \end{pmatrix}, \quad A^{s=0} = \frac{1}{2} \begin{pmatrix} -1&0\\ 0&1 \end{pmatrix},\quad A^{s=-1} = \frac{1}{\sqrt{2}}\begin{pmatrix} 0& 0 \\ -1 &0 \end{pmatrix},\\[.2cm] g_i = \sum_{s_i=-1,0,1} A^{s_i}\ket{s_i} = \frac{1}{\sqrt{2}} \begin{pmatrix} -\ket{0}_i & \sqrt{2}\ket{1}_i \\ -\sqrt{2}\ket{-1}_i & \ket{0}_i \end{pmatrix}. \end{gather*}\]

4.3. 边缘态

之前我们的讨论都是基于周期性边界条件，如果我们考虑开边界条件下的 AKLT 模型，显然首尾两端的自旋-1/2 粒子的自旋状态并不确定，因此 AKLT 模型的基态是四重简并的。

这一点从 $\eqref{OBC}$ 我们也可以具体看出来，其中 $\alpha_1,\beta_N$ 都是不固定的，而

\[\begin{equation} \ket{\Phi_{\mathrm{AKLT}}^{\mathrm{OBC}}(\uparrow\uparrow)}, \quad \ket{\Phi_{\mathrm{AKLT}}^{\mathrm{OBC}}(\uparrow\downarrow)},\quad \ket{\Phi_{\mathrm{AKLT}}^{\mathrm{OBC}}(\downarrow\uparrow)},\quad \ket{\Phi_{\mathrm{AKLT}}^{\mathrm{OBC}}(\downarrow\downarrow)} \end{equation}\]

是线性独立的四个基态，基态子空间的简并度其实就是由边界两个自旋-1/2 粒子来决定的，这也是 AKLT 模型所体现出的新奇的性质——整数自旋 $s=1$ 的自旋链，在边界处会出现半整数自旋 $s=1/2$ 的自由度，它也是边缘态的一个典型例子。这类边缘态普遍出现在具有某种拓扑性质的量子多体系统中，体现了拓扑保护下的量子相变或长程纠缠。这种特征不仅在自旋链中常见，还在广泛的拓扑相系统中展现出稳健的边界效应¹²。

5. 参考文献

1. Bethe H. Zur Theorie der Metalle. Z. Physik 71, 205–226 (1931). ↩︎

2. F. D. M. Haldane. Continuum dynamics of the 1-D Heisenberg antiferromagnet: Identification with the O(3) nonlinear sigma model. Physics Letters A, 93(9): 464-468 (1983). ↩︎

3. Z.-C. Gu, and X.-G. Wen. Tensor-entanglement-filtering renormalization approach and symmetry-protected topological order. Phys. Rev.B, (80):155131 (2009). ↩︎

4. C. K. Majumdar, D. K. Ghosh. On next nearest-neighbor interaction in linear chain. I, II. J. Math. Phys. 10, 1388–1402 (1969). ↩︎

5. W.J. Caspers, K.M. Emmett, W. Magnus, The Majumdar-Ghosh chain. Twofold ground state and elementary excitations. J. Phys. A: Math. Gen. 17, 2687 (1984). ↩︎

6. I. Affleck, T. Kennedy, E. H. Lieb, and H. Tasaki. Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev.Lett., (59):799 (1987). ↩︎

7. I. Affleck, T. Kennedy, E. H. Lieb, H. Tasaki, Valence bond ground states in isotropic quantum antiferromagnets. Commun. Math. Phys. 115,477–528 (1988). ↩︎

8. S. Knabe, Energy gaps and elementary excitations for certain VBS-quantum antiferromagnets. J. Stat. Phys. 52, 627–638 (1988). ↩︎

9. S. Michalakis, J.P. Zwolak, Stability of frustration-free hamiltonians. Commun. Math. Phys. 322, 277–302 (2013). ↩︎

10. H. Tasaki. Physics and mathematics of quantum many-body systems. Berlin: Springer, (2020). ↩︎ ↩︎²

11. R. Orus. A Practical Introduction to Tensor Networks: Matrix Product States and Projected Entangled Pair States. arXiv:1306.2164 [cond-mat.str-el] (2013). ↩︎

12. X.-G. Wen, Quantum Field Theory of Many-Body Systems: From the Origin of Sound to an Origin of Light and Electrons. Oxford University Press, Oxford, (2007). ↩︎