Derivation of General Formula for the Clebsch-Gordan Coefficients
1. Introduction
The addition of angular momenta is a fundamental problem in modern physics. For instance, when dealing with systems composed of multiple particles, such as atoms with multiple electrons, the total angular momentum of system is crucial. Specifically, we often inquire about how to add the orbital angular momentum and intrinsic spin momentum of an electron.
In this post, we will discuss the addition of two angular momenta for a quantum system and provide the general formula for the Clebsch-Gordan coefficients (CG coefficients). These coefficients are numbers that relate the total angular momentum eigenstates to the uncoupled tensor product basis.
2. Total angular momentum and state space
Consider a system formed by the union of two subsystems. The two angular momentum operators $\hat{\mathbf{J}}_1$ and $\hat{\mathbf{J}}_2$ are in different subspaces $V(j_1)$ and $V(j_2)$ respectively. We assume that $\hat{\mathbf{J}}_1$ and $\hat{\mathbf{J}}_2$ are independent, both of them satisfies the usual commutation relations
\[\begin{equation} [\hat{J}_{nk},\hat{J}_{nl}] = i\hbar \epsilon_{klm} \hat{J}_{nm}, \quad \text{where $n\in\{1,2\}$ and $k,l,m\in\{1,2,3\}$}. \end{equation}\]We choose the basis ${\ket{j_1,m_1}}$ of subspace $V(j_1)$ as the common eigenvectors of \(\hat{\mathbf{J}}_1^2\) and \(\hat{J}_{1z}\). Note that they are orthogonal and complete. And we define the rasing \(\hat{J}_{1+}\) and lowering \(\hat{J}_{1-}\) operators as \(\hat{J}_{1\pm} = \hat{J}_{1x}\pm i \hat{J}_{1y}\),
\[\begin{align} \hat{\mathbf{J}}_1^2 \ket{j_1,m_1} &= j_1(j_1+1)\hbar^2 \ket{j_1,m_1},\\[.3cm] \hat{J}_{1z}\ket{j_1,m_1}&=m_1\hbar \ket{j_1,m_1},\\[.3cm] \hat{J}_{1\pm} \ket{j_1,m_1}&=\hbar\sqrt{(j_1\mp m_1)(j_1\pm m_1 +1)}\ket{j_1,m_1\pm 1}. \end{align}\]Similarly for subsystem $(j_2)$,
\[\begin{align} \hat{\mathbf{J}}_2^2 \ket{j_2,m_2} &= j_2(j_2+1)\hbar^2 \ket{j_2,m_2},\\[.3cm] \hat{J}_{2z}\ket{j_2,m_2}&=m_2\hbar \ket{j_2,m_2},\\[.3cm] \hat{J}_{2\pm} \ket{j_2,m_2}&=\hbar\sqrt{(j_2\mp m_2)(j_2\pm m_2 +1)}\ket{j_2,m_2\pm 1}. \end{align}\]The state space of the global system is the tensor product of these two subspaces $V(j_1)$ and $V(j_2)$:
\[\begin{equation} V(J) = V(j_1) \otimes V(j_2). \end{equation}\]So we can get basis of the global state space by taking the direct product of the basis of the two subspaces. They are uncoupled basis and are denoted as ${\ket{j_1,m_1,j_2,m_2}}$,
\[\begin{equation} \ket{j_1,m_1,j_2,m_2} = \ket{j_1,m_1}\otimes\ket{j_2,m_2}. \end{equation}\]The space $V(J)$ is $(2j_1+1)(2j_2+1)$-dimensional since $V(j_1)$ is $(2j_1+1)$-dimensional and $V(j_2)$ is $(2j_2+1)$-dimensional.
The total angular momentum is defined as:
\[\begin{equation} \fcolorbox{#0070BF}{#F4FFF6}{ $\hat{\mathbf{J}} =\hat{\mathbf{J}}_1 \otimes \mathbb{1} + \mathbb{1}\otimes\hat{\mathbf{J}}_2 $.} \end{equation}\]where $\mathbb{1}$ denotes the identity operator. Sometimes we abbreviate it as $\hat{\mathbf{J}} = \hat{\mathbf{J}}_1 + \hat{\mathbf{J}}_2$. It is easy to show that the total angular momentum $\hat{\mathbf{J}}$ satisfies the angular momentum commutation relations
\[\begin{equation} [\hat{J}_{k},\hat{J}_{l}] = i\hbar\epsilon_{klm} \hat{J}_{m}. \end{equation}\]At this point, the angular momentum operators $\hat{\mathbf{J}}_1$ and $\hat{\mathbf{J}}_2$ should be understood as $\hat{\mathbf{J}}_1\otimes \mathbb{1}$ and $\mathbb{1}\otimes \hat{\mathbf{J}}_2$ respectively. Then we can obtain the following commutation relation
\[\begin{align} [\hat{J}_{z},\hat{\mathbf{J}}_1^2] &= [\hat{J}_z,\hat{\mathbf{J}}_2^2] =0,\\[.3cm] [\hat{\mathbf{J}}^2,\hat{\mathbf{J}}_1^2] & = [\hat{\mathbf{J}}^2,\hat{\mathbf{J}}_2^2] =0,\\[.3cm] [\hat{J}_{1z},\hat{J}_z] &= [\hat{J}_{2z},\hat{J}_z]=0. \end{align}\]The uncoupled basis ${\ket{j_1,m_1,j_2,m_2}}$ are simultaneous eigenstate of the operators \(\hat{\mathbf{J}}_1^2\), \(\hat{\mathbf{J}}_2^2\), \(\hat{J}_{1z}\) and \(\hat{J}_{2z}\). In this representation, it is more convenient to study the properties of each subsystem. This is also why they are called as uncoupled basis, so
\[\begin{align} \hat{\mathbf{J}}_1^2 \ket{j_1,m_1,j_2,m_2} &= j_1(j_1+1)\hbar^2\ket{j_1,m_1,j_2,m_2},\\[.3cm] \hat{\mathbf{J}}_2^2 \ket{j_1,m_1,j_2,m_2} &= j_2(j_2+1)\hbar^2\ket{j_1,m_1,j_2,m_2},\\[.3cm] \hat{J}_{1z} \ket{j_1,m_1,j_2,m_2}&=m_1\hbar\ket{j_1,m_1,j_2,m_2},\\[.3cm] \hat{J}_{2z} \ket{j_1,m_1,j_2,m_2}&=m_2\hbar\ket{j_1,m_1,j_2,m_2}. \end{align}\]But we find $\hat{\mathbf{J}}_1^2$, $\hat{\mathbf{J}}_2^2$, $\hat{\mathbf{J}}^2$ and $\hat{J}_z$ also commute. So they must have common eigenstates, which we will label them as ${\ket{j_1,j_2,J,M}}$. They are coupled basis of the global state space, note that they are distinct from the uncoupled basis. And we can find
\[\begin{align} \hat{\mathbf{J}}_1^2 \ket{j_1,j_2,J,M} & = j_1(j_1+1)\hbar^2\ket{j_1,j_2,J,M}, \\[.3cm] \hat{\mathbf{J}}_2^2 \ket{j_1,j_2,J,M} & = j_2(j_2+1)\hbar^2\ket{j_1,j_2,J,M}, \\[.3cm] \hat{\mathbf{J}}^2\ket{j_1,j_2,J,M} & = J(J+1)\hbar^2 \ket{j_1,j_2,J,M}, \\[.3cm] \hat{J}_z \ket{j_1,j_2,J,M} & = M\hbar \ket{j_1,j_2,J,M}, \end{align}\]where $M = m_1+m_2$ and $|j_1-j_2| \leq J \leq j_1+j_2$. And we can similarly define the ladder operator $\hat{J}_{\pm} = \hat{J}_x \pm i \hat{J}_y$ for total angular momentum, so
\[\begin{equation} \hat{J}_{\pm} \ket{j_1,j_2,J,M} = \hbar\sqrt{(J\mp M)(J\pm M+1)}\ket{j_1,j_2,J,M}. \end{equation}\]The total number of coupled basis must equal to the dimension of $V(J)$, and this is indeed the case since
\[\sum_{J=|j_1-j_2|}^{j_1+j_2} \underbrace{(2J+1)}_{\text{The number of $M$ for fixed $J$}} = (2j_1+1)(2j_2+1).\]Whether it is the uncoupled basis or the coupled basis, they both span the same vector space (state space for global system). The key formula to understand this is
\[\begin{equation} \fcolorbox{#0070BF}{#F4FFF6}{$ V(j_1)\otimes V(j_2) = V(j_1+j_2)\oplus V(j_1+j_2-1)\oplus \cdots \oplus V(|j_1-j_2|) $.} \end{equation}\]These two basis can be connected through unitary transformations
\[\begin{equation} \begin{split} \ket{j_1,j_2,J,M} &= \sum_{m_1=-j_1}^{j_1} \sum_{m_2=-j_2}^{j_2} \ket{j_1,m_1,j_2,m_2}\color{MediumBlue}{\braket{j_1,m_1,j_2,m_2}{j_1,j_2,J,M}} \\[.3cm] &= \sum_{m_1=-j_1}^{j_1}\sum_{m_2=-j_2}^{j_2} {\color{MediumBlue}{C_{j_1 m_1 j_2 m_2}^{JM}}} \ket{j_1,m_1,j_2,m_2}. \end{split} \end{equation}\]The coefficients \(C_{j_1m_1j_2m_2}^{JM} = \braket{j_1,m_1,j_2,m_2}{ j_1,j_2,J,M}\) of these expansions are called Clebsch-Gordan coefficients (CG coefficients). It is obvious that the CG coefficients can only be nonzero when
\[\begin{gather*} |j_1-j_2|\leq J \leq j_1+j_2,\\[.3cm] M = m_1+m_2. \end{gather*}\]Note that the definition of CG coefficients can not determine their values completely, they still have an arbitrary phase. We can, however, impose a convention to ensure that all CG coefficients are real,
\[\begin{aligned} C_{j_1j_1j_2j_2}^{j_1+j_2,j_1+j_2}&=\braket{j_1,j_1,j_2,j_2}{j_1,j_2,j_1+j_2,j_1+j_2}=1,\\[.3cm] C_{j_1j_1j_2,J-j_1}^{J,J}&=\braket{j_1,j_1,j_2,J-j_1}{j_1,j_2,J,J}>0. \end{aligned} \quad \text{Convention}\]Thus, $\braket{j_1,m_1,j_2,m_2}{ j_1,j_2,J,M} = \braket{j_1,j_2,J,M}{ j_1,m_1,j_2,m_2}$.
3. Orthogonality relations and recursion relations
Because the uncoupled basis and coupled basis are both individually orthogonal and complete, we can directly obtain two orthogonal relations for the CG coefficients, which means
\[\begin{aligned} \delta_{J' J}\delta_{M'M}&=\braket{j_1,j_2,J',M'}{j_1,j_2,J,M}\\[.3cm] &=\sum_{m_1}\sum_{m_2}\braket{j_1,j_2,J',M'}{j_1,m_1,j_2,m_2}\braket{j_1,m_1,j_2,m_2}{j_1,j_2,J,M}\\[.3cm] &=\sum_{m_1}\sum_{m_2}\braket{j_1,m_1,j_2,m_2}{j_1,j_2,J',M'}\braket{j_1,m_1,j_2,m_2}{j_1,j_2,J,M}, \end{aligned}\]or we can write it as
\[\begin{equation} \textcolor{Teal}{ \sum_{m_1}\sum_{m_2}C_{j_1m_1j_2m_2}^{J'M'}C_{j_1m_1j_2m_2}^{JM}=\delta_{J'J}\delta_{M'M}.\quad \text{Orthogonality relation (I)}} \end{equation}\]And
\[\begin{aligned} \delta_{m_1'm_1}\delta_{m_2'm_2} & = \braket{j_1,m_1',j_2,m_2'}{j_1,m_1,j_2,m_2}\\[.3cm] &=\sum_{J}\sum_{M}\braket{j_1,m_1',j_2,m_2'}{j_1,j_2,J,M}\braket{j_1,j_2,J,M}{j_1,m_1,j_2,m_2}\\[.3cm] &=\sum_{J}\sum_{M}\braket{j_1,m_1',j_2,m_2'}{j_1,j_2,J,M}\braket{j_1,m_1,j_2,m_2}{j_1,j_2,J,M}. \end{aligned}\]So
\[\begin{equation} \textcolor{Teal}{ \sum_{J}\sum_{M}C_{j_1m_1'j_2m_2'}^{JM}C_{j_1m_1j_2m_2}^{JM}=\delta_{m_1'm_1}\delta_{m_2'm_2}.\quad \text{Orthogonality relation (II) }} \end{equation}\]Utilizing total angular momentum ladder operators \(\hat{J}_{\pm} = \hat{J}_{1\pm} + \hat{J}_{2\pm}\), we can derive recursion relations for the CG coefficients.
\[\braket{j_1,m_1,j_2,m_2}{\hat{J}_{\pm}|j_1,j_2,J,M} = \mel{j_1,m_1,j_2,m_2}{(\hat{J}_{1\pm} + \hat{J}_{2\pm})}{j_1,j_2,J,M}.\]So
\[\begin{align*} &\sqrt{(J\mp M)(J\pm M+1)} \braket{j_1,m_1,j_2,m_2}{j_1,j_2,J,M\pm 1}\\[.3cm] ={}&\sqrt{(j_1\pm m_1)(j_1\mp m_1+1)} \braket{j_1,m_1\mp 1,j_2,m_2}{j_1,j_2,J,M}\\[.3cm] +{}& \sqrt{(j_2\pm m_2)(j_2\mp m_2+1)}\braket{j_1,m_1,j_2.m_2\mp 1}{j_1,j_2,J,M}. \end{align*}\]From this equation, we can obtain the recursion relations of CG coefficients
\[\textcolor{Teal}{ \begin{align} &\sqrt{(J-M)(J+M+1)}C_{j_1m_1j_2m_2}^{J,M+1} \qquad \text{Recursion relation (I)}\notag\\[.3cm] ={}& \sqrt{(j_1+m_1)(j_1-m_1+1)}C_{j_1,m_1-1,j_2m_2}^{JM} + \sqrt{(j_2+m_2)(j_2-m_2+1)}C_{j_1m_1j_2,m_2-1}^{JM}, \\[.6cm] &\sqrt{(J+M)(J-M+1)}C_{j_1m_1j_2m_2}^{J,M-1}\qquad \text{Recursion relation (II)}\notag\\[.3cm] ={}&\sqrt{(j_1-m_1)(j_1+m_1+1)}C_{j_1,m_1+1,j_2m_2}^{JM}+\sqrt{(j_2-m_2)(j_2+m_2+1)}C_{j_1m_1j_2,m_2+1}^{JM}. \end{align} }\]4. General expression for the Clebsch-Gordan coefficients
Using the previously obtained recursion relations and orthogonality relations, in this section, we will derive the general expression for CG coefficients. Note that we are adopting the convention mentioned earlier so that the CG coefficients are uniquely determined.
From the recursion relation (I), let $M=J$, the left hand side of the equation becomes zero, so
\[\sqrt{(j_1+m_1)(j_1-m_1+1)}C_{j_1,m_1-1,j_2m_2}^{JJ} + \sqrt{(j_2+m_2)(j_2-m_2+1)}C_{j_1m_1j_2,m_2-1}^{JJ} =0.\]Then let $m_1 \to m_1+1$, we can get another recursion relation
\[\begin{equation} C_{j_1 m_1 j_2 m_2}^{JJ} = -\sqrt{\frac{(j_2+m_2)(j_2-m_2+1)}{(j_1-m_1)(j_1+m_1+1)}} C_{j_1,m_1+1,j_2,m_2-1}^{JJ}. \label{equ:30} \end{equation}\]In $\eqref{equ:30}$, let $m_1\to m_1+1,m_2\to m_2-1$,
\[C_{j_1,m_1+1,j_2,m_2-1}^{JJ} = -\sqrt{\frac{[j_2+(m_2-1)][j_2-(m_2-1)+1]}{[j_1-(m_1+1)][j_1+(m_1+1)+1]}}C_{j_1,m_1+2,j_2,m_2-2}^{JJ}.\]Similarly,
\[\begin{gather*} C_{j_1,m_1+2,j_2,m_2-2}^{JJ} = -\sqrt{\frac{[j_2+(m_2-2)][j_2-(m_2-2)+1]}{[j_1-(m_1+2)][j_1+(m_1+2)+1]}}C_{j_1,m_1+3,j_2,m_2-3}^{JJ},\\[.3cm] \vdots\\[.3cm] C_{j_1,j_1-1,j_2,J-j_1+1}^{JJ} = - \sqrt{\frac{[j_2+(m_2-j_1+m_1+1)][j_2-(m_2-j_1+m_1+1)+1]}{[j_1-(m_1+j_1-m_1-1)][j_1+(m_1+j_1-m_1-1)+1]}} C_{j_1j_1 j_2 J-j_1}^{JJ}. \end{gather*}\]Note that we have already applied the selection rule $M = J = m_1+m_2$. Through repeated substitutions, we can obtain
\[\begin{align*} C_{j_1 m_1 j_2 m_2} &= (-1)^{j_1-m_1} \delta_{m_1+m_2,J}\\[.3cm] &\times \sqrt{\frac{(j_2+m_2)(j_2-m_2+1)}{(j_1-m_1)(j_1+m_1+1)}} \sqrt{\frac{[j_2+(m_2-1)][(j_2-(m_2-1)+1)]}{[j_1-(m_1+1)][j_1+(m_1+1)+1]}}\cdots \\[.3cm] &\times \sqrt{\frac{[j_2+(m_2-j_1+m_1+1)][j_2-(m_2-j_1+m_1+1)+1]}{[j_1-(m_1+j_1-m_1-1)][j_1+(m_1+j_1-m_1-1)+1]}} C_{j_1j_1 j_2,J-j_1}^{JJ}, \end{align*}\]where
\[\prod_{k=0}^{j_1-m_1-1} (j_2+m_2-k) = \frac{(j_2+m_2)!}{(j_2-j_1+m_1+m_2)!} = \frac{(j_2+m_2)!}{(j_2-j_1+J)!},\]and
\[\begin{align*} \prod_{k=0}^{j_1-m_1-1}[j_2-(m_2-k)+1] &= \frac{(j_1+j_2-J)!}{(j_2-m_2)!},\\[.3cm] \prod_{k=0}^{j_1-m_1-1}(j_1-m_1-k)&=(j_1-m_1)!,\\[.3cm] \prod_{k=0}^{j_1-m_1-1}[j_1+(m_1+k)+1] & = \frac{(2J)!}{(j_1+m_1)!}. \end{align*}\]Thus, we have
\[\begin{equation} C_{j_1m_1j_2m_2}^{JJ}= (-1)^{j_1-m_1}\delta_{m_1+m_2,J}\times \sqrt{\frac{(j_1+m_1)!(j_2+m_2)!}{(j_1-m_1)!(j_2-m_2)!}} \sqrt{\frac{(j_1+j_2-J)!}{(J+j_2-j_1)!(2J)!}} C_{j_1j_1j_2,J-j_1}^{JJ}. \label{equ:31} \end{equation}\]Since we know that
\[\ket{j_1,j_2,J,J} = \sum_{m_1}\sum_{m_2}C_{j_1m_1j_2m_2}^{JJ}\ket{j_1,m_1,j_2,m_2}, \quad \braket{j_1,j_2,J,J}{j_1,j_2,J,J} =1,\]which means $\sum_{m_1}\sum_{m_2} \vert C_{j_1m_1j_2m_2}^{JJ}\vert^2 =1$. So
\[\left[\sum_{m_1}\sum_{m_2}\frac{(j_1+m_1)!(j_2+m_2)!}{(j_1-m_1)!(j_2-m_2)!}\delta_{m_1+m_2,J}\right] \times \frac{(j_1+j_2-J)!}{(J+j_2-j_1)!(2J)!} |C_{j_1j_1j_2,J-j_1}^{JJ}|^2=1.\]One of the summation can be canceled, it can be simplified as
\[\left[\sum_{m_1} \frac{(j_1+m_1)!(j_2+J-m_1)!}{(j_1-m_1)!(j_2-J+m_1)!}\right] \times \frac{(j_1+j_2-J)!}{(J+j_2-j_1)!(2J)!} |C_{j_1j_1j_2,J-j_1}^{JJ}|^2 =1.\]The summation can be shown to be:
\[\begin{equation} \textcolor{ForestGreen}{\sum_{m_1=-j_1}^{j_1} \frac{(j_1+m_1)!(j_2+J-m_1)!}{(j_1-m_1)!(j_2-J+m_1)!} = \frac{(j_1+j_2+J+1)!(J+j_1-j_2)!(j_2+J-j_1)!}{(j_1+j_2-J)!(2J+1)!}}. \end{equation}\]Q. How to prove it?
According to our previous convention, where $C_{j_1 j_1 j_2 ,J-j_1}^{JJ}>0$, we can derive an important result
\[\begin{equation} C_{j_1 j_1 j_2,J-j_1}^{JJ} = \sqrt{\frac{(2J)!(2J+1)!}{(j_1+j_2+J+1)!(J+j_1-j_2)!}}. \end{equation}\]Substituting it into $\eqref{equ:31}$, we can obtain
\[\begin{align} C_{j_1m_1j_2m_2}^{JJ} &= (-1)^{j_1-m_1} \delta_{m_1+m_2,J}\notag \\[.3cm] &\times \sqrt{\frac{(j_1+m_1)!(j_2+m_2)!}{(j_1-m_1)!(j_2-m_2)!}} \sqrt{\frac{(j_2+j_2-J)!(2J+1)!}{(J+j_2-j_1)!(j_1+j_2+J+1)!(J+j_1-j_2)!}},\label{equ:34} \end{align}\]which also means
\[\begin{align*} &\ket{j_1,j_2,J,J}\\[.3cm] ={}&\sum_{m_1}\sum_{m_2} \ket{j_1,m_1,j_2,m_2} (-1)^{j_1-m_1} \delta_{m_1+m_2,J} \sqrt{\frac{(j_1+m_1)!(j_2+m_2)!}{(j_1-m_1)!(j_2-m_2)!}} \sqrt{\frac{(j_1+j_2-J)!(2J+1)!}{(J+j_2-j_1)!(j_1+j_2+J+1)!(J+j_1-j_2)!}}\\[.3cm] ={}&\sum_{m_1} \ket{j_1,m_1,j_2,J-m_1} (-1)^{j_1-m_1}\sqrt{\frac{(j_1+m_1)!(j_2+J-m_1)!}{(j_1-m_1)!(j_2-J+m_1)!}}\sqrt{\frac{(j_1+j_2-J)!(2J+1)!}{(J+j_2-j_1)!(j_1+j_2+J+1)!(J+j_1-j_2)!}}. \end{align*}\]Now we want to derive the general CG coefficient $C_{j_1m_2j_2m_2}^{JM} = \braket{j_1,m_1,j_2,m_2}{ j_1,j_2,J,M}$, note that
\[\begin{equation} \ket{j_1,j_2,J,M} = \sqrt{\frac{(J+M)!}{(2J)!(J-M)!}}(\hat{J}_{-})^{J-M} \ket{j_1,j_2,J,J}, \end{equation}\]so
\[C_{j_1m_1j_2m_2}^{JM} = \delta_{m_1+m_2,M}\sqrt{\frac{(J+M)!}{(2J)!(J-M)!}} \mel{j_1,m_1,j_2,m_2}{(\hat{J}_{-})^{J-M}}{j_1,j_2,J,J}.\]To calculate \(\bra{j_1,m_1,j_2,m_2}(\hat{J}_{-})^{J-M}\), we just need calculate \((\hat{J}_{+})^{J-M}\ket{j_1,m_1,j_2,m_2}\),
\[\begin{align*} &(\hat{J}_{+})^{J-M} \ket{j_1,m_1,j_2,m_2} \\[.3cm] ={}& (\hat{J}_{1+}+\hat{J}_{2+})^{J-M} \ket{j_1,m_1}\ket{j_2,m_2}\\[.3cm] ={}&\sum_{k=0}^{J-M} \frac{(J-M)!}{(k!)(J-M-K)!} (\hat{J}_{1+})^{k}\ket{j_1,m_1} (\hat{J}_{2+})^{J-M-k}\ket{j_2,m_2}\\[.3cm] ={}&\sum_{k=0}^{J-M} \frac{(J-M)!}{k!(J-M-k)!}\sqrt{\frac{(j_1-m_1)!(j_1+m_1+k)!}{(j_1+m_1)!(j_1-m_1-k)!}}\sqrt{\frac{(j_2-m_2)!(j_2+m_2+J-M-k)!}{(j_2+m_2)!(j_2-m_2-J+M+k)!}} \ket{j_1,m_1+k} \ket{j_2,m_2+J-M+k}. \end{align*}\]Taking its conjugate and substituting it back into the previous expression, we have
\[\begin{align*} &\mel{j_1,m_1,j_2,m_2}{(\hat{J}_{-})^{J-M}}{j_1,j_2,J,J}\\[.3cm] ={}&\sum_{k=0}^{J-M} \frac{(J-M)!}{k! (J-M-k)!} \sqrt{\frac{(j_1-m_1)!(j_1+m_1+k)!}{(j_1+m_1)!(j_1-m_1-k)!}}\\[.3cm] \times{}& \sqrt{\frac{(j_2-m_2)!(j_2+m_2+J-M-k)!}{(j_2+m_2)!(j_2-m_2-J+M+k)!}} \braket{j_1,m_1+k,j_2,m_2+J-M-k}{ j_1,j_2,J,J}. \end{align*}\]Utilizing the result from $\eqref{equ:34}$, we obtain the final expression for the CG coefficients
\[\begin{equation} \textcolor{red}{ \begin{split} C_{j_1m_1j_2m_2}^{JM}&=C_{j_1m_2j_2,M-m_1}^{JM}\\[.3cm] &=\delta_{m_1+m_2,M}\sqrt{\frac{(2J+1)(j_1+j_2-J)!}{(j_1+j_2+J+1)!(j_1+J-j_2)!(j_2+J-j_1)!}} \\[.3cm] &\times\sqrt{\frac{(j_1-m_1)!(j_2+m_1-M)!(J+M)!(J-M)!}{(j_1+m_1)!(j_2+M-m_1)!}}\\[.3cm] &\times \sum_{k=0}^{J-M}(-1)^{j_1-m_1-k} \frac{(j_1+m_1+k)!(j_2+J-m_1-k)!}{k!(J-M-k)!(j_1-m_1-k)!(j_2-J+m_1+k)!}. \end{split}} \end{equation}\]This is exactly the result provided by Edmonds (1955). Or we can write it in a more symmetric expression (Racah, 1942):
\[\begin{equation} \textcolor{red}{ \begin{split} C_{j_1m_1j_2m_2}^{JM}&=C_{j_1m_2j_2,M-m_1}^{JM}\\[.3cm] &=\delta_{m_1+m_2,M} \sqrt{\frac{(2J+1)(J+j_1-j_2)!(J-j_1+j_2)!(j_1+j_2-J)!}{(j_1+j_2+J+1)!}}\\[.3cm] &\times \sqrt{(J+M)!(J-M)!(j_1-m_1)!(j_1+m_1)!(j_2-m_2)!(j_2+m_2)!} \\[.3cm] &\times\sum_{k}\frac{(-1)^k}{k!(j_1+j_2-J-k)!(j_1-m_1-k)!(j_2+m_2-k)!(J-j_2+m_1+k)!(J-j_1-m_2+k)!}. \end{split}} \end{equation}\]The summation is extended over all integer $k$ for which the argument of every factorial is nonnegative.
5. Symmetry properties
Here, we list some symmetry properties of CG coefficients, which can be proven using either the recursion relations or the general expression for CG coefficients.
\[\begin{align} &C_{JMJ,-M}^{00} = \frac{(-1)^{J-M}}{\sqrt{2J+1}},\\[.3cm] &C_{JM00}^{JM}=1,\\[.3cm] &C_{j_1m_1j_2m_2}^{JM} =(-1)^{j_1+j_2-J} C_{j_2m_2j_1m_1}^{JM},\\[.3cm] &C_{j_1,-m_1,j_2,-m_2}^{J,-M}=(-1)^{j_1+j_2-J} C_{j_1m_1j_2m_2}^{JM},\\[.3cm] &C_{j_1m_1j_2m_2}^{j_3m_3}=(-1)^{j_2+m_2} \sqrt{\frac{2j_3+1}{2j_1+1}} C_{j_2,-m_2,j_3m_3}^{j_1m_1},\\[.3cm] &C_{j_1m_1j_2m_2}^{j_3m_3} =(-1)^{j_1-m_1} \sqrt{\frac{2j_3+1}{2j_2+1}} C_{j_3m_3j_1,-m_1}^{j_2m_2}. \end{align}\]6. CG coefficients table
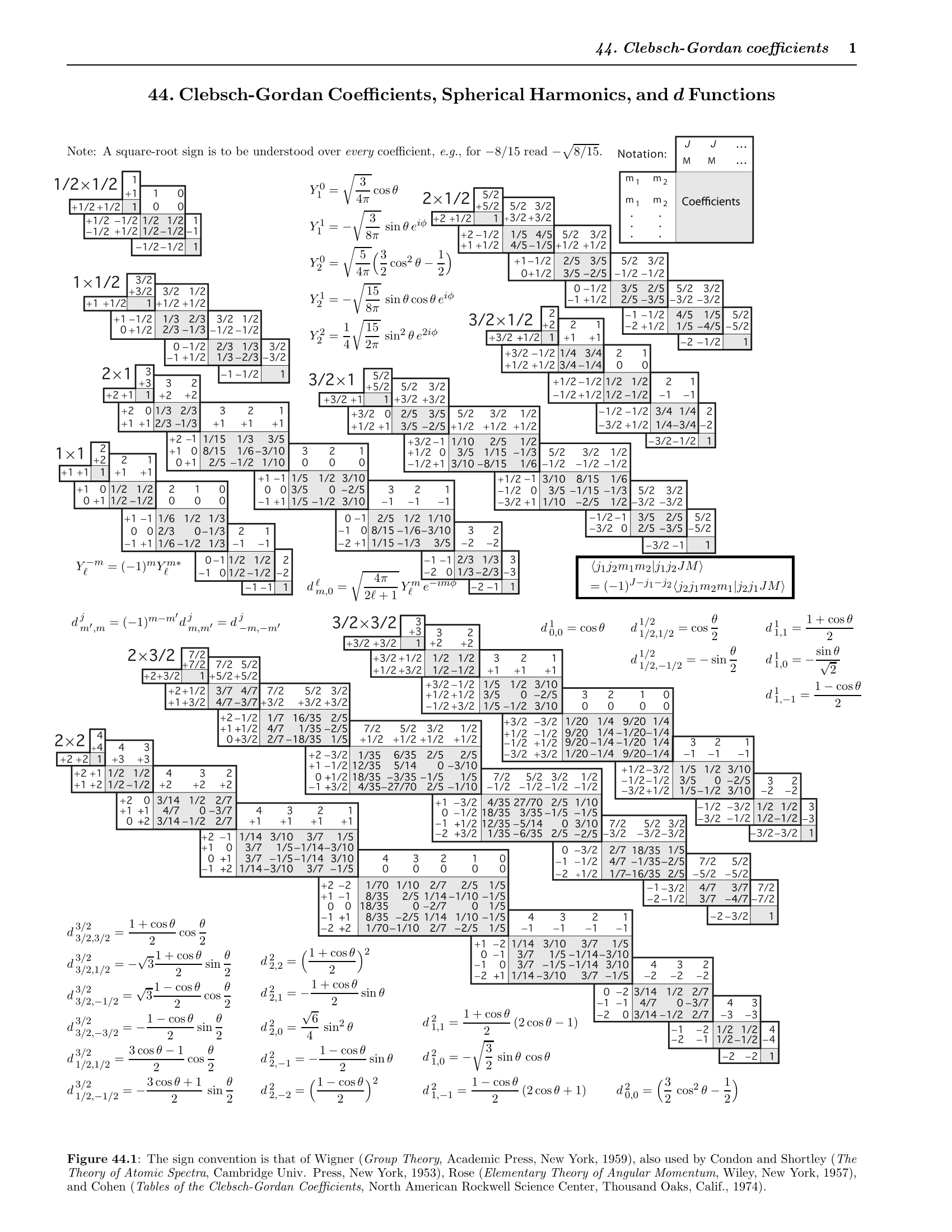
Below are partial tables of CG coefficients. You can get the corresponding CG coefficients from the tables directly.
However, using Mathematica makes it more convenient. You can simply use the command ClebschGordan[{j1,m1},{j2,m2},{J,M}] to obtain the corresponding CG coefficients. For example, calculate $C_{5040}^{10}$,
1
2
In:= ClebschGordan[{5,0},{4,0},{1,0}]
Out:= sqrt{5/33}
7. References
- [1] A. R. Edmonds. Angular Momentum in Quantum Mechanics. Princeton University Press. 1996
- [2] J. J. Sakurai, Jim Napolitano. Modern Quantum Mechanics. Cambridge University Press. 2020
- [3] Claude Cohen-Tannoudji, Bernard Diu, Franck Laloë. Quantum Mechanics, Volume 2: Angular Momentum, Spin, and Approximation Methods. Wiley-VCH. 2019
- [4] 金彪. 高等量子力学讲义. 2023年秋