§2.1 Single-Particle Green's Functions at Zero Temperature

Hamiltonian with interaction can not always be solved exactly, the first few orders of perturbation theory cannot provide an adequate description of an interacting many-particle system. So we must find other methods to obtain all orders in perturbation theory. Luckily, we can get a formal solution through Green’s functions.

1. Definition, symmetry and physical significance of the single-particle Green’s functions

1.1. Definition

Single-particle Green's function

The single-particle Green’s function is defined as:

\[\begin{equation} G_{\alpha\beta}(\vb{x},t;\vb{x}',t') := -i \bra{\psi_{H}^{0}} \hat{\mathsf{T}}\qty[\hat{\psi}_{H\alpha}(\vb{x},t)\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')]\ket{\psi_H^{0}}, \end{equation}\]

where $\ket{\psi_{H}^{0}}$ is the Heisenberg ground state of the interacting system satisfying

\[\begin{equation} \hat{H} \ket{\psi_{H}^0} = E_g^{0} \ket{\psi_H^0}, \quad \braket{\psi_H^0} =1. \end{equation}\]

And $\hat{\psi}_{H\alpha}(\vb{x},t)$ is a Heisenberg operator with the time dependence

\[\begin{equation} \hat{\psi}_{H\alpha}(\vb{x},t) = \e^{i\hat{H}(t-t_0)/\hbar} \hat{\psi}_{\alpha}(\vb{x}) \e^{-i\hat{H}(t-t_0)/\hbar}. \end{equation}\]

The $\hat{T}$ product here represents a generalization of the time-ordering operator,

\[\begin{equation} \hat{\mathsf{T}} [\hat{\psi}_{H\alpha}(\vb{x},t)\hat{\psi}_{H\beta}^{\dagger}(\vb{x}',t')] = \begin{cases} \hat{\psi}_{H\alpha}(\vb{x},t)\hat{\psi}_{H\beta}^\dagger(\vb{x}',t'), \quad & t>t',\\[.2cm] \pm\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')\hat{\psi}_{H\alpha}(\vb{x},t), & t'>t, \end{cases} \end{equation}\]

where the upper (lower) sign refers to bosons (fermions).

More generally, the $\hat{\mathsf{T}}$ product of several operators orders them from right to left in ascending time order and adds a factor $(-1)^{P}$, where $P$ is the number of interchanges of fermion operators from the original given order.

1.2. Symmetry

1. If the Hamiltonian does not depend on time which means that $\hat{H}(t) = \hat{H}$, then the Green’s function depends only on the time difference,

   \[\begin{equation} G_{\alpha\beta}(\vb{x},t;\vb{x}',t') = G_{\alpha\beta}(\vb{x},\vb{x}';t-t'). \end{equation}\]

2. If the system is translational invariance (i.e. $[\hat{H},\hat{\mathbf{P}}] = 0$), then the Green’s function depends only on the position difference,

   \[\begin{equation} G_{\alpha\beta}(\vb{x},t;\vb{x}',t') = G_{\alpha\beta}(\vb{x}-\vb{x}';t,t'). \end{equation}\]
   Proof of 1. and 2.

   Here we just prove the case of fermions. Expand the definition of the Green’s function,

   \[\begin{align*} i G_{\alpha\beta}(\vb{x},t;\vb{x}',t')& = \ev{\hat{\mathsf{T}}\qty[\hat{\psi}_{H\alpha}(\vb{x},t)\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')]}{\psi_{H}^0}\\[.2cm] &=\ev{\hat{\mathsf{T}}\qty[\e^{i\hat{H}t/\hbar}\hat{\psi}_{\alpha}(\vb{x})\e^{-i\hat{H}t/\hbar}\e^{i\hat{H}t'/\hbar}\hat{\psi}_{\beta}^\dagger(\vb{x}')\e^{-i\hat{H}t'/\hbar}]}{\psi_H^0}\\[.2cm] &=\theta(t-t') \ev{\e^{i\hat{H}t/\hbar}\hat{\psi}_{\alpha}(\vb{x})\e^{-i\hat{H}t/\hbar}\e^{i\hat{H}t'/\hbar}\hat{\psi}_{\beta}^\dagger(\vb{x}')\e^{-i\hat{H}t'/\hbar}}{\psi_H^0}\\[.2cm] &\qquad -\theta(t'-t)\ev{\e^{i\hat{H}t'/\hbar}\hat{\psi}_{\beta}^\dagger(\vb{x}')\e^{-i\hat{H}t'/\hbar} \e^{i\hat{H}t/\hbar}\hat{\psi}_{\alpha}(\vb{x})\e^{-i\hat{H}t/\hbar}}{\psi_H^0}\\[.2cm] &=\theta(t-t')\e^{i\omega_g t}\ev{\hat{\psi}_{\alpha}(\vb{x})\e^{-i\hat{H}t/\hbar}\e^{i\hat{H}t'/\hbar}\hat{\psi}_{\beta}^\dagger(\vb{x}')}{\psi_H^0}\e^{-i\omega_g t'}\\[.2cm] &\qquad -\theta(t'-t) \e^{i\omega_g t'} \ev{\hat{\psi}_{\beta}^\dagger(\vb{x}')\e^{-i\hat{H}t'/\hbar} \e^{i\hat{H}t/\hbar}\hat{\psi}_{\alpha}(\vb{x})}{\psi_H^0} \e^{-i\omega_g t}\\[.2cm] &=\theta(t-t') \ev{\hat{\psi}_{\alpha}(\vb{x})\e^{-i \hat{H}(t-t')/\hbar}\hat{\psi}_{\beta}^\dagger(\vb{x}')}{\psi_H^0}\e^{i\omega_g(t-t')}\\[.2cm] &\qquad - \theta(t'-t) \ev{\hat{\psi}_{\beta}^\dagger(\vb{x}' \e^{i\hat{H}(t-t')/\hbar}\hat{\psi}_{\alpha}(\vb{x}))}{\psi_H^0}\e^{-i\omega_g(t-t')}. \end{align*}\]

   It is obviously to see that the Green’s function only depend on the time difference $t-t’$. Since the total momentum operator commute with $\hat{H}$, they have common eigenstates

   \[\hat{H} \ket{E_g,\mathbf{P}} = E_g \ket{E_g,\mathbf{P}},\quad \hat{\mathbf{P}}\ket{ E_g, \mathbf{P}} = \mathbf{P}\ket{E_g,\mathbf{P}}.\]

   For ground state, we have

   \[\hat{H}\ket{\psi_H^0} = E_g \ket{\psi_H^0}, \quad \hat{\mathbf{P}} \ket{\psi_H^0} = 0.\]

   And we find

   \[\begin{align*} [\hat{\psi}_{\alpha}(\vb{x}),\hat{\mathbf{P}}]&= \qty[\hat{\psi}_{\alpha}(\vb{x}),\sum_{\beta}\int \dd[3]{x'}\hat{\psi}_{\beta}^\dagger(\vb{x}')(-i\hbar \nabla)\hat{\psi}_{\beta}(\vb{x}')]\\[.2cm] &=\sum_{\beta} \int\dd[3]{x'} \qty[\hat{\psi}_{\alpha}(\vb{x}), \hat{\psi}_{\beta}^\dagger(\vb{x}')(-i\hbar \nabla_{\vb{x}'})\hat{\psi}_{\beta}(\vb{x}')]\\[.2cm] &=\sum_{\beta} \int\dd[3]{x'} \qty{\qty[\hat{\psi}_{\alpha}(\vb{x}),\hat{\psi}_{\beta}^\dagger(\vb{x}')]_+ (-i\hbar\nabla_{\vb{x}'})\hat{\psi}_{\beta}(\vb{x}') - \hat{\psi}_{\beta}(\vb{x}') \qty[\hat{\psi}_{\alpha}(\vb{x}),-i\hbar\nabla_{\vb{x}'}\hat{\psi}_{\beta}(\vb{x}')]_+ }\\[.2cm] &=\sum_{\beta} \int \dd[3]{x'} \qty[\delta(\vb{x}-\vb{x}') \delta_{\alpha\beta}(-i\hbar\nabla_{\vb{x}'})\hat{\psi}_{\beta}(\vb{x}') - \hat{\psi}_{\beta}^\dagger(\vb{x}')(-i\hbar \nabla_{\vb{x}'})\times 0]\\[.2cm] &= -i\hbar \nabla\hat{\psi}_{\alpha}(\vb{x}). \end{align*}\]

   This relation is true for both bosons and fermions. Its solution is

   \[\hat{\psi}_{\alpha}(\vb{x}) = \e^{-i\hat{\mathbf{P}}\cdot \mathbf{x}/\hbar}\hat{\psi}_{\alpha}(0) \e^{i\hat{\mathbf{P}}\cdot \mathbf{x}/\hbar},\quad \hat{\psi}_{\alpha}^\dagger(\vb{x}) = \e^{-i\hat{\mathbf{P}}\cdot \mathbf{x}/\hbar} \hat{\psi}^\dagger_{\alpha}(0) \e^{i\hat{\mathbf{P}}\cdot \mathbf{x}/\hbar}.\]

   Then we can rewrite the Green’s function as

   \[\begin{align*} i G_{\alpha\beta}(\vb{x},t;\vb{x}',t') & = \theta(t-t') \ev{\e^{-i\hat{\mathbf{P}}\cdot\mathbf{x}/\hbar}\hat{\psi}_{\alpha}(0)\e^{i\hat{\mathbf{P}}\cdot\mathbf{x}/\hbar}\e^{-i\hat{H}(t-t')/\hbar}\e^{-i\hat{\mathbf{P}}\cdot\mathbf{x}'/\hbar}\hat{\psi}_{\beta}^\dagger(0)\e^{i\hat{\mathbf{P}}\cdot\mathbf{x}'/\hbar}}{\psi_H^0}\e^{i\omega_{g}(t-t')}\\[.2cm] &\quad - \theta(t'-t) \ev{\e^{-i\hat{\mathbf{P}}\cdot\mathbf{x}'/\hbar}\hat{\psi}_{\beta}^\dagger(0)\e^{i\hat{\mathbf{P}}\cdot\mathbf{x}'/\hbar} \e^{i\hat{H}(t-t')/\hbar} \e^{-i\hat{\mathbf{P}}\cdot\mathbf{x}/\hbar}\hat{\psi}_{\alpha}(0)\e^{i\hat{\mathbf{P}}\cdot\mathbf{x}/\hbar}}{\psi_H^0}\e^{-i\omega_{g}(t-t')}\\[.2cm] &=\theta(t-t')\ev{\hat{\psi}_{\alpha}(0)\e^{i\hat{\mathbf{P}}\cdot(\mathbf{x}-\mathbf{x}')/\hbar}\e^{-i\hat{H}(t-t')/\hbar}\hat{\psi}_{\beta}^\dagger(0)}{\psi_H^0}\e^{-i\mathbf{P}\cdot(\mathbf{x}-\mathbf{x}')/\hbar}\e^{i\omega_{g}(t-t')}\\[.2cm] &\quad - \theta(t'-t)\ev{\hat{\psi}_{\beta}^\dagger(0)\e^{-i\hat{\mathbf{P}}\cdot(\mathbf{x}-\mathbf{x}')/\hbar}\e^{i\hat{H}(t-t')/\hbar}\hat{\psi}_{\alpha}^(0)}{\psi_H^0}\e^{i\mathbf{P}\cdot(\mathbf{x}-\mathbf{x}')/\hbar}\e^{i\omega_{g}(t-t')}, \end{align*}\]

   where we have used $[\hat{H},\hat{\mathbf{P}}]=0$. So it also only depend on the position difference $\mathbf{x}-\mathbf{x}’$. Thus $G_{\alpha\beta}(\vb{x},t;\vb{x}’,t’) = G_{\alpha\beta}(\vb{x}-\vb{x}’,t-t’)$. The same is true for the bosons.

   ∎

3. If the Hamiltonian is independent of particle’s spin, then

   \[\begin{equation} G_{\alpha\beta}(\vb{x},t;\vb{x}',t') = G(\vb{x},t;\vb{x}',t')\delta_{\alpha\beta}. \end{equation}\]

   And if $\alpha=\beta$, then $G_{\alpha\alpha}(\vb{x},t;\vb{x}’,t’) = G(\vb{x},t;\vb{x}’,t’)$. Assume the spin quantum number is $s$, then $\hat{S}^2 = s(s+1)$ and $\displaystyle{\sum_{\alpha}1 = 2s+1}$, so

   \[\begin{equation} G(\vb{x},t;\vb{x}',t') = \frac{1}{2s+1}\sum_{\alpha} G_{\alpha\alpha}(\vb{x},t;\vb{x}',t'). \end{equation}\]

4. If all three conditions above are met, then

   \[\begin{equation} G_{\alpha\beta}(\vb{x},t;\vb{x}',t') = G(\vb{x}-\vb{x}',t-t')\delta_{\alpha\beta}. \end{equation}\]

1.3. Physical significance

Without loss of generality, we can assume $t>t’$ and let $t_0 = 0$, then the Green’s function becomes

\[\begin{align*} G_{\alpha\beta}(\vb{x},t;\vb{x}',t') &\propto \mel{\psi_H^0}{\hat{\psi}_{\alpha}(\vb{x},t)\hat{\psi}_\beta^\dagger(\vb{x}',t')}{\psi_H^0}\\[.2cm] &= \mel{\psi_H^0}{\e^{i\hat{H}t/\hbar}\hat{\psi_{\alpha}}(\vb{x})\e^{-i\hat{H}t/\hbar} \e^{i\hat{H}t'/\hbar}\hat{\psi}_{\beta}^\dagger(\vb{x}')\e^{-i\hat{H}t'/\hbar}}{\psi_H^0}\\[.2cm] &=\underbrace{\langle \psi_H^0 | \e^{i\hat{H}t/\hbar}}_{\bra{\Phi_2}} \ \underbrace{\hat{\psi}_{\alpha}(\vb{x})\e^{-i\hat{H}(t-t')/\hbar} \hat{\psi}_{\beta}^\dagger(\vb{x}')\e^{-i\hat{H}t'/\hbar} | \psi_H^{0} \rangle}_{\ket{\Phi_1}}. \end{align*}\]

Starting from the ground state $\ket{\psi_{H}^0}$, $\e^{-i\hat{H} t’/\hbar}$ represents the evolution to time $t’$. If we apply the field operator $\hat{\psi}_{\beta}^{\dagger}(\vb{x}’)$ to this state $\e^{-i\hat{H} t’/\hbar}\ket{\psi_{H}^0}$, it means that a particle with spin index $\beta$ is created at position $\vb{x}’$. Finally, let this state evolve from time $t’$ to $t$ and let the particle created at time $t’$ be annihilated by $\hat{\psi}_{\alpha}(\vb{x})$ at $\vb{x}$ with a spin index $\alpha$. So we reach the state $\ket{\Phi_1} = \hat{\psi}_{\alpha}(\vb{x})\e^{-i\hat{H}(t-t’)/\hbar} \hat{\psi}_{\beta}^\dagger(\vb{x}’)\e^{-i\hat{H}t’/\hbar}\ket{\psi_H^0}$.

Similarly for the state $\bra{\Phi_2}$. Starting from the ground state $\bra{\psi_H^0}$, after evolving to time $t$, we get the state $\bra{\Phi_2} = \bra{\psi_H^0}\e^{i\hat{H}t/\hbar}$.

So Green’s function is actually proportional to this probability amplitude $\braket{\Phi_2}{\Phi_1}$. That’s why Green’s function is also called as propagator.

2. Relation to observables

2.1. Ground state expectation value of single-particle operators

The expectation value of any single-particle operator in the ground state of the system can be expressed via Green’s function.

The ground state expectation value of a single-particle operator

\[\begin{equation} \mel{\psi_H^0}{\hat{F}^{(1)}}{\psi_H^0} = \pm i \sum_{\alpha}\sum_\beta \int \dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \hat{f}_{\alpha\beta}(\vb{x},-i\hbar\nabla,\hat{s}) G_{\alpha\beta}(\vb{x},t;\vb{x}',t'), \end{equation}\]

where the upper (lower) sign refers to bosons (fermions).

Proof

Recall the previous section, we have obtained the expression of single-particle operator in second quantization:

\[\begin{equation*} \hat{F}^{(1)} = \sum_{\alpha}\sum_{\beta}\int \dd[3]{x} \hat{\psi}^\dagger_{\alpha}(\vb{x}) \mel{\alpha}{\hat{f}(\vb{x},\hat{p},\hat{s})}{\beta}\hat{\psi}_{\beta}(\vb{x}). \end{equation*}\]

Then the ground state of a single operator $\hat{F}^{(1)}$ can be expressed as

\[\begin{align*} \mel{\psi_H^0}{\hat{F}^{(1)}}{\psi_H^0} & = \sum_{\alpha}\sum_{\beta} \int \dd[3]{x} \mel{\psi_H^0}{\hat{\psi}^\dagger_{\alpha}(\vb{x}) \hat{f}_{\alpha\beta}(\vb{x},-i\hbar\nabla,\hat{s})\hat{\psi}_{\beta}(\vb{x})}{\psi_H^0}\\[.2cm] &=\sum_{\alpha}\sum_{\beta} \int \dd[3]{x} \lim_{\vb{x}'\to \vb{x}} \hat{f}_{\alpha\beta}(\vb{x},-i\hbar\nabla,\hat{s}) \\[.2cm] &\qquad \times \mel{\psi_{H}^0}{\cancelto{\e^{-iE_g t/\hbar}}{\e^{-i\hat{H}t/\hbar}}\hat{\psi}_{H\alpha}(\vb{x},t)^\dagger \cancel{\e^{i\hat{H}t/\hbar}}\cancel{\e^{-i\hat{H}t/\hbar}}\hat{\psi}_{H\beta}(\vb{x},t)\cancelto{\e^{iE_g t/\hbar}}{\e^{i\hat{H}t/\hbar}}}{\psi_{H_0}}\\[.2cm] &=\sum_{\alpha}\sum_{\beta} \int \dd[3]{x} \lim_{\vb{x}'\to\vb{x}} \hat{f}_{\alpha\beta}(\vb{x},-i\hbar\nabla,\hat{s}) \mel{\psi_H^0}{\hat{\psi}_{H\alpha}^\dagger(\vb{x}',t)\hat{\psi}_{H\beta}(\vb{x},t)}{\psi_H^0}\\[.2cm] &=\sum_{\alpha}\sum_{\beta} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \hat{f}_{\alpha\beta}(\vb{x},-i\hbar\nabla,\hat{s}) \mel{\psi_H^0}{\hat{\psi}_{H\alpha}^\dagger(\vb{x}',t')\hat{\psi}_{H\beta}(\vb{x},t)}{\psi_H^0} \end{align*}\]

Note that $\hat{A}(t’)\hat{B}(t) = \hat{\mathsf{T}}\left[\hat{A}(t’)\hat{B}(t)\right]$ if $t’>t$. And

\[\hat{\mathsf{T}}\qty[\hat{A}(t')\hat{B}(t)] = \hat{\mathsf{T}}\qty[\pm \hat{B}(t)\hat{A}(t')] = \pm \hat{\mathsf{T}}\qty[\hat{B}(t)\hat{A}(t)'],\]

where the upper (lower) sign refers to bosons (fermions). Then

\[\begin{align*} \mel{\psi_H^0}{\hat{F}^{(1)}}{\psi_H^0} & = \sum_{\alpha}\sum_{\beta} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \hat{f}_{\alpha\beta}(\vb{x},-i\hbar\nabla,\hat{s}) \mel{\psi_H^0}{\hat{\mathsf{T}}\qty[\hat{\psi}_{H\alpha}^\dagger(\vb{x}',t')\hat{\psi}_{H\beta}(\vb{x},t)]}{\psi_H^0}\\[.2cm] &=\pm \sum_{\alpha}\sum_{\beta} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \hat{f}_{\alpha\beta}(\vb{x},-i\hbar\nabla,\hat{s}) \mel{\psi_H^0}{\hat{\mathsf{T}}\qty[\hat{\psi}_{H\beta}(\vb{x},t)\hat{\psi}_{H\alpha}^\dagger(\vb{x}',t')]}{\psi_H^0}\\[.2cm] &= \pm \sum_{\alpha}\sum_{\beta} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \hat{f}_{\alpha\beta}(\vb{x},-i\hbar\nabla,\hat{s}) G_{\beta\alpha}(\vb{x},t;\vb{x}',t')\\[.2cm] &= \pm \sum_{\alpha}\sum_{\beta} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \hat{f}_{\alpha\beta}(\vb{x},-i\hbar\nabla,\hat{s}) G_{\alpha\beta}(\vb{x},t;\vb{x}',t'). \end{align*}\]

∎

If $\hat{f}_{\alpha\beta} = \mel{\alpha}{\hat{f}}{\beta}$ is independent of particle’s spin, i.e. $\hat{f}_{\alpha\beta} = \hat{f}\delta_{\alpha\beta}$, then

\[\begin{equation} \ev{\hat{F}^{(1)}}{\psi_H^0} = \pm i\sum_{\alpha}\int\dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \hat{f}(\vb{x},-i\hbar\nabla) G_{\alpha\alpha}(\vb{x},t;\vb{x}',t'). \end{equation}\]

Examples

• For total kinetic energy operator:

  \[\begin{align} \ev{\hat{T}}{\psi_H^0} &= \pm i \sum_{\alpha}\sum_{\beta} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \delta_{\alpha\beta}\qty(-\frac{\hbar^2\nabla^2}{2m}) G_{\alpha\beta}(\vb{x},t;\vb{x}',t')\notag\\[.2cm] &= \pm i \sum_{\alpha} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \qty(-\frac{\hbar^2\nabla^2}{2m}) G_{\alpha\alpha}(\vb{x},t;\vb{x}',t'). \label{Total kinetic energy} \end{align}\]

• For total momentum operator:

  \[\begin{align} \ev{\hat{\mathbf{P}}}{\psi_H^0} = \pm i \sum_{\alpha} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} (-i\hbar\nabla)G_{\alpha\alpha}(\vb{x},t;\vb{x}',t'). \end{align}\]

• For local density operator:

  \[\begin{align} \ev{\hat{n}(\vb{y})}{\psi_H^0} &= \sum_{\alpha} \ev{\hat{\psi}_{\alpha}^\dagger(\vb{y}) \hat{\psi}_{\alpha}(\vb{y})}{\psi_H^0}\notag\\[.2cm] &= \sum_{\alpha} \ev{\hat{\psi}_{H\alpha}(\vb{y},t)\hat{\psi}_{H\alpha}(\vb{y},y)}{\psi_H^0}\notag\\[.2cm] &= \sum_{\alpha} \lim_{\substack{\vb{y}'\to\vb{y}\\ t'\to t^+}} \ev{\hat{\psi}_{H\alpha}^\dagger(\vb{y}',y')\hat{\psi}_{H\alpha}(\vb{y},t)}{\psi_H^0}\notag\\[.2cm] &=\pm i \sum_{\alpha}\lim_{\substack{\vb{y}'\to\vb{y}\\ t'\to t^+}} G_{\alpha\alpha}(\vb{y},t;\vb{y}',t'). \end{align}\]

  And total particle number operator:

  \[\begin{align} \ev{\hat{N}}{\psi_H^0} &= \ev{\int\dd[3]y\ \hat{n}(\vb{y})}{\psi_H^0}\notag =\int \dd[3]{y} \ev{\hat{n}(\vb{y})}{\psi_H^0}\notag\\[.2cm] &=\pm i \sum_{\alpha} \int \dd[3]{y} \lim_{\substack{\vb{y}'\to\vb{y}\\ t'\to t^+}} G_{\alpha\alpha}(\vb{y},t;\vb{y}',t'). \end{align}\]

• For spin density operator:

  \[\begin{align} \ev{\hat{s}(\vb{y})}{\psi_H^0}= \pm i \sum_{\alpha\beta} \mel{\alpha}{\hat{s}}{\beta} \lim_{\substack{\vb{y}'\to\vb{y}\\ t'\to t^+}} G_{\beta\alpha}(\vb{y},t;\vb{y}',t'). \end{align}\]

  And total spin operator:

  \[\begin{align} \ev{\hat{S}}{\psi_H^0} = \pm i \sum_{\alpha}\sum_\beta \mel{\alpha}{\hat{s}}{\beta} \int \dd[3]{y} \lim_{\substack{\vb{y}'\to\vb{y}\\ t'\to t^+}} G_{\beta\alpha}(\vb{y},t;\vb{y}',t'). \end{align}\]

• For electrical current density operator:

  \[\begin{align} \ev{\hat{\mathbf{J}}(\vb{x})}{\psi_H^0} &= -\frac{ie\hbar}{2m} \sum_{\alpha} \qty{ \ev{\hat{\psi}_{\alpha}^\dagger(\vb{x})\nabla \hat{\psi}_{\alpha}(\vb{x})}{\psi_H^0} - \ev{\qty(\nabla \hat{\psi}_{\alpha}^\dagger(\vb{x}))\hat{\psi}_{\alpha}(\vb{x})}{\psi_H^0} }\notag\\[.2cm] &=-\frac{ie\hbar}{2m} \sum_{\alpha} \begin{aligned}[t] &\Big\{\ev{\hat{\psi}_{H\alpha}(\vb{x},t)\nabla\hat{\psi}_{H\alpha}(\vb{x},t)}{\psi_H^0}\\[.2cm] &\quad -\ev{\qty(\nabla \hat{\psi}_{H\alpha}^\dagger(\vb{x},t))\hat{\psi}_{H\alpha}(\vb{x},t)}{\psi_H^0}\Big\} \end{aligned} \notag\\[.2cm] &=-\frac{ie\hbar}{2m}\sum_{\alpha} \begin{aligned}[t] &\Big\{ \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \nabla_{\vb{x}} \ev{\hat{\psi}_{H\alpha}^\dagger(\vb{x}',t')\hat{\psi_{H\alpha}(\vb{x},t)}}{\psi_H^0}\\ &\quad-\lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \nabla_{\vb{x}'} \ev{\hat{\psi}_{H\alpha}(\vb{x}',t')\hat{\psi}_{H\alpha}(\vb{x},t)}{\psi_H^0}\Big\} \end{aligned}\notag\\[.2cm] &=-\frac{ie\hbar}{2m} \cdot \pm i \sum_{\alpha} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \qty(\nabla_{\vb{x}} - \nabla_{\vb{x}'}) G_{\alpha\alpha}(\vb{x},t;\vb{x}',t')\notag\\[.2cm] &=\pm \frac{e\hbar}{2m} \sum_{\alpha} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \qty(\nabla_{\vb{x}} - \nabla_{\vb{x}'}) G_{\alpha\alpha}(\vb{x},t;\vb{x}',t'). \end{align}\]

2.2. Ground state energy

We have obtain the total kinetic energy of ground state in $\eqref{Total kinetic energy}$, so what about the potential energy $\langle\hat{V}\rangle$ and thereby determine the total ground state energy? The Hamiltonian $\hat{H}=\hat{H}_0+\hat{V}$ of system in second quantization is

\[\begin{align*} \hat{H} &= \sum_{\alpha} \int \dd[3]{x} \hat{\psi}_{\alpha}^\dagger(\vb{x}) \qty(-\frac{\hbar^2 \nabla^2}{2m})\hat{\psi}_{\alpha}(\vb{x}) \\[.2cm] &\qquad \qquad+ \frac{1}{2}\sum_{\alpha\alpha'\beta\beta'} \int\dd[3]{x}\dd[3]{x'} \hat{\psi}^\dagger_{\alpha}(\vb{x})\hat{\psi}^\dagger_{\beta}(\vb{x}') V_{\alpha\alpha',\beta\beta'}(\vb{x},\vb{x}')\hat{\psi}_{\beta'}(\vb{x}')\hat{\psi}_{\alpha'}(\vb{x}'). \end{align*}\]

We assume that $\hat{V}$ is a two-particle operator which is independent of particles’ spin. The ground state energy can be expressed as

\[\begin{equation} E_g = \ev{\hat{H}}{\psi_H^0} = \ev{\hat{H_0}}{\psi_H^0} + \ev{\hat{V}}{\psi_{H}^0}. \end{equation}\]

where

\[\begin{align} \ev{\hat{H_0}}{\psi_H^0} &= \ev{\hat{T}_k}{\psi_H^0} = \pm i \sum_{\alpha} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to \vb{x}\\ t'\to t^+}} \qty(-\frac{\hbar^2 \nabla^2}{2m}) G_{\alpha\alpha}(\vb{x},t;\vb{x}',t'),\\[.2cm] \ev{\hat{V}}{\psi_H^0} &= \pm \frac{i}{2} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to \vb{x}\\ t'\to t^+}} \sum_{\alpha} \qty[i\hbar \pdv{t} + \frac{\hbar^2 \nabla^2}{2m}] G_{\alpha\alpha}(\vb{x},t;\vb{x}',t'). \end{align}\]

The ground state energy

Then we can express the total ground state energy solely in terms of the single-particle Green’s function,

\[\begin{equation} E_g = \pm \frac{i}{2} \sum_{\alpha} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to \vb{x}\\ t'\to t^+}} \qty(i\hbar \pdv{t}- \frac{\hbar^2 \nabla^2}{2m}) G_{\alpha\alpha}(\vb{x},t;\vb{x}',t'). \label{ground state energy} \end{equation}\]

Proof

Consider the Heisenberg equation of Heisenberg field operator $\hat{\psi}_{H\alpha}(\vb{x},t)$:

\[\begin{equation*} i\hbar \pdv{t} \hat{\psi}_{H\alpha}(\vb{x},t) =[\hat{\psi}_{H\alpha}(\vb{x},t),\hat{H}] = \e^{i\hat{H}t/\hbar}[\hat{\psi}_{\alpha}(\vb{x}),\hat{H}]\e^{-i\hat{H}t/\hbar}, \end{equation*}\]

where

\[\begin{align*} [\hat{\psi}_{\alpha}(\vb{x}),\hat{H}] &= \sum_{\beta} \int\dd[3]{z} [\hat{\psi}_{\alpha}(\vb{x}),\hat{\psi}_{\beta}^\dagger(\vb{z}) \hat{T}_k \hat{\psi}_{\beta}(\vb{z})] + \frac{1}{2}\sum_{\beta\beta'\gamma\gamma'} \int\dd[3]{z}\dd[3]{z'}\\[.2cm] &\qquad\quad \times \qty[\hat{\psi}_{\alpha}(\vb{x}),\hat{\psi}_{\beta}^\dagger(\vb{z}) \hat{\psi}_{\gamma}^\dagger(\vb{z}')V_{\beta\beta',\gamma\gamma'}(\vb{z},\vb{z}')\hat{\psi}_{\gamma'}(\vb{z}')\hat{\psi}_{\beta'}(\vb{z})]. \end{align*}\]

For definiteness, consider the fermion case which is more complicated, so

\[\begin{align*} [\hat{\psi}_{\alpha}(\vb{x}),\hat{H}] &= \hat{T}_k(\vb{x})\hat{\psi}_{\alpha}(\vb{x}) -\frac{1}{2} \sum_{\beta\beta'\gamma'}\int \dd[3]{z}\hat{\psi}_{\beta}^\dagger(\vb{z}) V_{\beta\beta',\alpha\gamma'}(\vb{z},\vb{x})\hat{\psi}_{\gamma'}(\vb{x})\hat{\psi}_{\beta'}(\vb{z})\\[.2cm] &\qquad\quad + \frac{1}{2} \sum_{\beta'\gamma\gamma'}\int\dd[3]{z'}\hat{\psi}_{\gamma}^\dagger(\vb{z}')V_{\alpha\beta',\gamma\gamma'}(\vb{x},\vb{z}') \hat{\psi}_{\gamma'}(\vb{z}')\hat{\psi}_{\beta'}(\vb{x})\\[.2cm] &= \hat{T}_{k}(\vb{x})\hat{\psi}_{\alpha}(\vb{x}) + \sum_{\beta'\gamma\gamma'}\int\dd[3]{z'}\hat{\psi}_{\gamma}^\dagger(\vb{z}')V_{\alpha\beta',\gamma\gamma'}(\vb{x},\vb{z}') \hat{\psi}_{\gamma'}(\vb{z}')\hat{\psi}_{\beta'}(\vb{x}). \end{align*}\]

So the Heisenberg equation becomes

\[\begin{align*} \qty(i\hbar \pdv{t} - \hat{T}_{k}(\vb{x}))\hat{\psi}_{H\alpha}(\vb{x},t) = \sum_{\beta\gamma\gamma'} \int \dd[3]{z'} \hat{\psi}_{H\gamma}(\vb{z}',t) V_{\alpha\beta',\gamma\gamma'}\hat{\psi}_{H\gamma'}(\vb{z}',t)\hat{\psi}_{H\beta'}(\vb{x},t). \end{align*}\]

Multiply both sides left by $\hat{\psi}_{H\alpha}^\dagger(\vb{x}’,t’)$ and then take the ground state expectation value

\[\begin{align*} &\qty(i\hbar \pdv{t}-\hat{T}_{k}(\vb{x})) \ev{\hat{\psi}^{\dagger}_{H\alpha}(\vb{x}',t')\hat{\psi}_{H\alpha}(\vb{x},t)}{\psi_H^0} \\[.2cm] ={}& \sum_{\beta'\gamma\gamma'} \int\dd[3]{z'} \ev{ \hat{\psi}_{H\alpha}^\dagger(\vb{x}',t')\hat{\psi}_{H\gamma}^\dagger(\vb{z'},t)V_{\alpha\beta',\gamma\gamma'}(\vb{x},\vb{z}') \hat{\psi}_{H\gamma'}(\vb{z}',t)\hat{\psi}_{H\beta'}(\vb{x},t) }{\psi_H^0}. \end{align*}\]

In the limit $\vb{x}’ \to \vb{x}, t’\to t^+$, integrating $\vb{x}$ and summing $\alpha$, then we get the expression for $\ev{\hat{V}}{\psi_H^0}$ in fermion case

\[\begin{align*} \ev{\hat{V}}{\psi_H^0} &=\qty(i\hbar \pdv{t} + \frac{\hbar^2 \nabla^2}{2m}) \int\dd[3]{x} \sum_{\alpha} \ev{\hat{\psi}_{H\alpha}^\dagger(\vb{x}',t')\hat{\psi}_{H\alpha}(\vb{x},t)}{\psi_H^0} \\[.2cm] &=-\frac{i}{2} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to \vb{x}\\ t'\to t^+}} \sum_{\alpha} \qty[i\hbar \pdv{t} + \frac{\hbar^2 \nabla^2}{2m}] G_{\alpha\alpha}(\vb{x},t;\vb{x}',t'). \end{align*}\]

For boson case, the negative sign becomes positive sign. Add the total kinetic energy, and we finally get the total ground state energy,

\[E_g = \pm \frac{i}{2} \sum_{\alpha} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to \vb{x}\\ t'\to t^+}} \qty(i\hbar\pdv{t}-\frac{\hbar^2 \nabla^2}{2m}) G_{\alpha\alpha}(\vb{x},t;\vb{x}',t').\]

∎

The ground state energy (with Hellman- Feynman theorem)

We can write the ground state energy in another form

\[\begin{equation} \begin{split} E_g &= E_g^ 0 + \int_0^{1} \frac{\dd{\lambda}}{\lambda} \ev{\lambda \hat{V}}{\psi_{H}^0(\lambda)}\\[.2cm] &= E_g^0 + \int_0 ^{1} \frac{\dd{\lambda}}{\lambda}\qty[ \pm \frac{i}{2} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to \vb{x}\\ t'\to t^+}} \sum_{\alpha} \qty[i\hbar \pdv{t} + \frac{\hbar^2 \nabla^2}{2m}] G_{\alpha\alpha}(\vb{x},t;\vb{x}',t'). ] \end{split} \end{equation}\]

where the Hamiltonian is written with a variable coupling constant $\lambda$ as $\hat{H}(\lambda) = \hat{T}_k + \lambda \hat{V}$. Then $\hat{H}(1) = \hat{H}$ and $\hat{H}(0) = \hat{H}_0 = \hat{T}_k$, $\hat{T}_k \ket{\phi^0} = E_g^0 \ket{\phi^0}$ where $\ket{\phi^0}$ is the ground state without interaction $\hat{V}$.

Proof

The time-independent Schrödinger equation for an arbitrary value $\lambda$ is

\[\hat{H}(\lambda) \ket{\psi_H^0(\lambda)} = E_g(\lambda) \ket{\psi_H^0}(\lambda).\]

Take the derivative of $\lambda$ on both sides, then

\[\begin{align*} \dv{\lambda}\qty[\hat{H}(\lambda)\ket{\psi_H^0(\lambda)}] &= \qty[\dv{\lambda}\hat{H}(\lambda)] \ket{\psi_H^0(\lambda)} + \hat{H}(\lambda)\qty[\dv{\lambda}\ket{\psi_H^0(\lambda)}],\\[.2cm] \dv{\lambda} \qty[E_g(\lambda) \ket{\psi_H^0(\lambda)}] &= \qty[\dv{\lambda} E_g(\lambda)] \ket{\psi_H^0(\lambda)} + E_g(\lambda)\qty[\dv{\lambda}\ket{\psi_H^0(\lambda)}]. \end{align*}\]

Multiply both sides left by $\bra{\psi_H^0(\lambda)}$,

\[\begin{align*} &\ev{\qty[\dv{\lambda}\hat{H}(\lambda)]}{\psi_H^0(\lambda)} + \cancel{\bra{\psi_H^0(\lambda)} \hat{H}(\lambda) \qty[\dv{\lambda}\ket{\psi_H^0(\lambda)}]} \\[.2cm] ={}& \ev{\qty[\dv{\lambda}E_g(\lambda)]}{\psi_H^0(\lambda)} + \cancel{E_g(\lambda) \bra{\psi_H^0(\lambda)} \qty[\dv{\lambda}\ket{\psi_H^0(\lambda)}]}. \end{align*}\]

Thus we have proof the Hellman-Feynman theorem,

\[\begin{equation*} \ev{\qty[\dv{\lambda}\hat{H}(\lambda)]}{\psi_H^0(\lambda)} = \dv{\lambda}E_g(\lambda) \end{equation*}\]

Substitute $\hat{H} = \hat{T}_k + \lambda \hat{V}$, then

\[\ev{\hat{V}}{\psi_H^0(\lambda)} = \dv{\lambda} E_g(\lambda) \quad \Rightarrow \quad \frac{1}{\lambda}\ev{\lambda\hat{V}}{\psi_H^0(\lambda)} = \dv{\lambda} E_g(\lambda).\]

Integrate $\lambda$ from zero to one on both sides and note that $E_g(0) = E_g^0$ and $E_g(1)=E_g$

\[E_g = E_g^ 0 + \int_0^{1} \frac{\dd{\lambda}}{\lambda} \ev{\lambda \hat{V}}{\psi_{H}^0(\lambda)}.\]

∎

If the Hamiltonian does not depend on time, and the system is homogeneous, we can write the ground state energy in a simpler form. First, take the Fourier transform of the single-particle Green’s function

\[\begin{equation} G_{\alpha\beta}(\vb{x}-\vb{x}',t-t') =\frac{1}{V} \sum_{\vb{k}}\int_{-\infty}^\infty \frac{\dd{\omega}}{2\pi} G_{\alpha\beta}(\vb{k},\omega) \e^{i\vb{k}\cdot (\vb{x}-\vb{x}')}\e^{-i\omega(t-t')}. \end{equation}\]

And the corresponding inverse Fourier transform is

\[\begin{equation} G_{\alpha\beta}(\vb{k},\omega) = \int\dd[3]{(x-x')} \int\dd{(t-t')} G_{\alpha\beta}(\vb{x}-\vb{x}',t-t')\e^{-ik\cdot(\vb{x}-\vb{x}')}\e^{i\omega(t-t')}. \end{equation}\]

Then the ground state energy is

\[\begin{align} E_g &= \pm \frac{i}{2} \sum_{\alpha}\int \dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}} \qty(i\hbar \pdv{t} - \frac{\hbar^2 \nabla^2}{2m}) G_{\alpha\alpha}(\vb{x}-\vb{x}',t-t')\notag\\[.2cm] &= \pm \frac{i}{2} \sum_{\alpha}\int\dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}}\qty(i\hbar \pdv{t} - \frac{\hbar^2 \nabla^2}{2m}) \qty{ \frac{1}{V} \sum_{\vb{k}}\int_{-\infty}^\infty \frac{\dd{\omega}}{2\pi} G_{\alpha\alpha}(\vb{k},\omega) \e^{i\vb{k}\cdot (\vb{x}-\vb{x}')}\e^{-i\omega(t-t')} }\notag\\[.2cm] &= \pm\frac{i}{2V} \sum_{\alpha} \int\dd[3]{x} \lim_{\substack{\vb{x}'\to\vb{x}\\ t'\to t^+}}\sum_{\vb{k}} \int_{-\infty}^{\infty} \frac{\dd{\omega}}{2\pi} \qty(\hbar\omega+\frac{\hbar^2k^2}{2m})G_{\alpha\alpha}(\vb{k},\omega) \e^{i\vb{k}\cdot (\vb{x}-\vb{x}')}\e^{-i\omega (t-t')}\notag\\[.2cm] &=\pm \frac{i}{2}\lim_{\eta\to 0^+}\sum_{\alpha}\sum_{\vb{k}}\int_{-\infty}^{\infty} \frac{\dd{\omega}}{2\pi} \qty(\hbar\omega + \frac{\hbar^2k^2}{2m}) G_{\alpha\alpha}(\vb{k},\omega)\e^{i\omega\eta}. \label{ground state energy in k} \end{align}\]

And another form of the ground state energy is

\[\begin{align} E_g &= E_g^0 \pm \frac{i}{2} \int_0^1 \frac{\dd{\lambda}}{\lambda} \int \dd[3]{x} \lim_{\substack{\vb{x}'\to \vb{x}\\ t'\to t^+}} \sum_{\alpha} \qty[i\hbar \pdv{t} + \frac{\hbar^2 \nabla^2}{2m}] G_{\alpha\alpha}(\vb{x},t;\vb{x}',t')\notag \\[.2cm] & = E_g^0 \pm \frac{i}{2} \int_0^{1} \frac{\dd\lambda}{\lambda}\lim_{\eta\to 0^+}\sum_{\alpha}\sum_{\vb{k}} \int_{-\infty}^{\infty} \frac{\dd\omega}{2\pi} \qty(\hbar \omega - \frac{\hbar^2 k^2}{2m})G_{\alpha\alpha}(\vb{k},\omega)\e^{i\omega\eta}. \end{align}\]

3. Free fermions

As an example of the above formalism, we will consider the single-particle Green’s function for a noninteracting homogeneous system of fermions. The Hamiltonian of the system is

\[\begin{equation} \hat{H} = \hat{T}_k = \sum_{\alpha} \int \dd[3]{x} \hat{\psi}_{\alpha}^\dagger(\vb{x}) \qty(-\frac{\hbar^2\nabla^2}{2m}) \hat{\psi}_{\alpha}(\vb{x}). \end{equation}\]

In plane wave representation, we have

\[\hat{\psi}_{\alpha}(\vb{x}) = \frac{1}{\sqrt{V}} \sum_{\vb{k}} \hat{C}_{\vb{k}\alpha} \e^{i\vb{k}\cdot\vb{x}}, \quad \hat{\psi}_{\alpha}^\dagger(\vb{x}) = \frac{1}{\sqrt{V}} \sum_{\vb{k}} \hat{C}_{\vb{k}\alpha} \e^{-i\vb{k}\cdot\vb{x}},\quad \hat{H} =\hat{T}_k= \sum_{\vb{k}\alpha} \epsilon_{\vb{k}}^0\hat{C}_{\vb{k}\alpha}^\dagger \hat{C}_{\vb{k}\alpha},\]

where $\epsilon_{\vb{k}}^0 = \hbar^2 k^2/2m$. The ground state is defined as

\[\begin{equation} \ket{\Phi^0} = \prod_{|\vb{k}|\leq k_{F}}\prod_{\alpha}\hat{C}_{\vb{k}\alpha}^\dagger\ket{0}, \quad \hat{H}\ket{\Phi^0} = \hat{T}_k\ket{\Phi^0} = E_g^0 \ket{\Phi^0}. \end{equation}\]

Then

\[\begin{align*} \sum_{\vb{k}}\sum_{\alpha}\hat{C}_{\vb{k}\alpha}^\dagger \hat{C}_{\vb{k}\alpha} \epsilon_\vb{k}^0 \ket{\Phi^0} = \sum_{\vb{k}}\sum_{\alpha} \hat{n}_{\vb{k}\alpha} \epsilon_{\vb{k}}^0 \ket{\Phi^0} = \sum_{\vb{k}}\sum_{\alpha}\epsilon_{\vb{k}}^0 \theta(k_F - |\vb{k}|) \ket{\Phi^0} = E_g^0 \ket{\Phi^0}, \end{align*}\]

where $\hat{n}_{\vb{k}\alpha} \ket{\Phi}^0 = \hat{C}_{\mathbf{k}\alpha}^\dagger\hat{C}_{\mathbf{k}\alpha} \ket{\Phi^0} = \theta(k_F - \abs{\vb{k}}) \ket{\Phi^0}$. So the ground state energy is

\[\begin{equation} E_g^0 = \sum_{\vb{k}}\sum_{\alpha} \theta(k_F- |\vb{k}|)\epsilon_{\vb{k}}^0 = \sum_{\abs{\vb{k}}\leq k_F}\sum_{\alpha} \epsilon_{\vb{k}}^0. \label{ground state energy for free fermions} \end{equation}\]

With box normalization which means that

\[\sum_{\vb{k}}(\cdots) = \frac{V}{(2\pi)^3} \int\dd[3]{k} (\cdots).\]

Then the summation of $\vb{k}$ can be converted to integral of $\vb{k}$

\[E_g^ 0 = \sum_{\alpha}\frac{V}{(2\pi)^3} \int \dd[3]{k} \theta(k_F- |\vb{k}|) \epsilon_{\vb{k}}^0 = \sum_{\alpha} \frac{V}{(2\pi)^3} 4\pi \int_0^{k_F} k^2 \dd{k} \frac{\hbar^2 k^2}{2m} = 2\frac{V}{(2\pi)^3} 4\pi \frac{1}{2m} \frac{\hbar^5 k_F^5}{5},\]

and $\ev{\hat{N}}{\Phi^0} = \sum_{\alpha}\frac{V}{(2\pi)^3}4\pi \frac{\hbar^3 k_F^3}{3} = N$, $E_F= \frac{\hbar^2 k_F^2}{2m}$. Thus the ground state energy of $E_g^0$ can be expressed as

\[\begin{equation} E_g^ 0 = \frac{3}{5}N E_F. \end{equation}\]

These are well-known results in previous study (solid state physics). Now we will use single-particle Green’s function to re-obtain above results to verify that our theory is correct. The single-particle Green’s function for fermions is defined as

\[\begin{align*} iG_{\alpha\beta}^0(\vb{x},t;\vb{x}',t') & = \ev{\hat{\mathsf{T}}\qty[\hat{\psi}_{H\alpha}(\vb{x},t),\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')]}{\Phi^0}\\[.2cm] &= \theta(t-t') \ev{\hat{\psi}_{H\alpha}(\vb{x},t)\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')}{\Phi^0} - \theta(t'-t) \ev{\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')\hat{\psi}_{H\alpha}(\vb{x},t)}{\Phi^0}, \end{align*}\]

where we use $G^0$ to represent the Green’s function of the noninteracting system. The field operator in Heisenberg picture is

\[\begin{align} \hat{\psi}_{H\alpha}(\vb{x},t) &= \e^{i\hat{T}_k t/\hbar} \hat{\psi}_{\alpha}(\vb{x}) \e^{-i \hat{T}_k t/\hbar}\notag\\[.2cm] &=\e^{i\hat{T}_k t/\hbar} \frac{1}{\sqrt{V}} \sum_{\vb{k}}\hat{C}_{\vb{k}\alpha} \e^{i\vb{k}\cdot\vb{x}} \e^{-i\hat{T}_k t/\hbar}\notag\\[.2cm] &=\frac{1}{\sqrt{V}} \sum_{\vb{k}} \e^{i\vb{k}\cdot\vb{x}} \e^{i\hat{T}_k t/\hbar} \hat{C}_{\vb{k}\alpha}\e^{-i\hat{T}_k t/\hbar} = \frac{1}{\sqrt{V}} \sum_{\mathbf{k}} \e^{i\vb{k}\cdot\vb{x}}\hat{C}_{H,\vb{k}\alpha}(t), \end{align}\]

where we have set $t_0 =0$. There are two methods to calculate $\hat{C}_{H,\vb{k}\alpha}(t) = \e^{i\hat{T}_k t/\hbar} \hat{C}_{\vb{k}\alpha}\e^{-i\hat{T}_k t/\hbar}$ which will be left as an exercise.

Exercise: Calculate $\hat{C}_{H,\vb{k}\alpha}$

1. Use Baker-Campbell-Hausdorff formula

   \[\e^{\lambda \hat{A}} \hat{B} \e^{-\lambda\hat{A}} = \sum_{n=0}^{\infty} \frac{\lambda^n}{n!} \hat{C}_n, \quad \text{where $\hat{C}_0 = \hat{B},\hat{C}_n = [\hat{A},\hat{C}_{n-1}]$.}\]

2. Solve Heisenberg equation with condition $\hat{C}_{H,\vb{k}\alpha}(t=0) = \hat{C}_{\vb{k}\alpha}$,

   \[i\hbar \pdv{t} \hat{C}_{H,\vb{k}\alpha} = [\hat{C}_{H,\vb{k}\alpha}, \hat{H}].\]

The result is

\[\begin{equation} \hat{C}_{H,\vb{k}\alpha}(t) = \hat{C}_{\vb{k}\alpha}\e^{-i\epsilon_{\vb{k}}^0 t/\hbar} = \hat{C}_{\vb{k}\alpha}\e^{-i\omega_{\mathbf{k}}t}, \end{equation}\]

where $\epsilon_{\mathbf{k}}^0 = \hbar\omega_{\mathbf{k}}$. Then

\[\begin{align*} iG_{\alpha\beta}^0 (\vb{x},t;\vb{x}',t') &= \begin{aligned}[t] &\theta(t-t') \frac{1}{V} \sum_{\vb{k}}\sum_{\vb{k}'}\ev{\hat{C}_{\vb{k}\alpha}\hat{C}_{\vb{k}'\beta}^\dagger}{\Phi^0} \e^{i\vb{k}\cdot\vb{x} - i \omega_{\vb{k}}t} \e^{-i\vb{k}'\cdot\vb{x}'+i\omega_{\vb{k}'} t'}\\[.2cm] -{}&\theta(t'-t)\frac{1}{V} \sum_{\mathbf{k}}\sum_{\mathbf{k}'}\ev{\hat{C}_{\mathbf{k}'\beta}^\dagger \hat{C}_{\mathbf{k}\alpha}}{\Phi^0} \e^{i\mathbf{k}\cdot\mathbf{x}- i\omega_{\mathbf{k}} t} \e^{-i\mathbf{k}'\cdot\mathbf{x}'+i\omega_{\mathbf{k}'}t'}, \end{aligned} \end{align*}\]

where

\[\begin{align*} \ev{\hat{C}_{\mathbf{k}\alpha}\hat{C}_{\mathbf{k}'\beta}^\dagger}{\Phi^0} &= \delta_{\mathbf{k}\mathbf{k}'}\delta_{\alpha\beta} \ev{\hat{C}_{\mathbf{k}\alpha}\hat{C}_{\mathbf{k}\alpha}^\dagger}{\Phi^0}\\[.2cm] &= \delta_{\mathbf{k}\mathbf{k}'} \delta_{\alpha\beta} \ev{\qty(1-\hat{C}_{\mathbf{k}\alpha}^\dagger\hat{C}_{\mathbf{k}\alpha})}{\Phi^0} \\[.2cm] &=\delta_{\mathbf{k}\mathbf{k}'}\delta_{\alpha\beta}\ev{1-\hat{n}_{\mathbf{k}\alpha}}{\Phi^0} = \delta_{\vb{k}\mathbf{k}'}\delta_{\alpha\beta}\theta(|\mathbf{k}|-k_F),\\[.2cm] \ev{\hat{C}_{\mathbf{k}'\beta}^\dagger\hat{C}_{\mathbf{k}\alpha}}{\Phi^0}& = \delta_{\mathbf{k}'\mathbf{k}}\delta_{\alpha\beta} \ev{\hat{C}_{\mathbf{k}\alpha}\hat{C}_{\mathbf{k\alpha}}}{\Phi^0} = \delta_{\mathbf{k}'\mathbf{k}}\delta_{\alpha\beta} \theta(k_{F}-\abs{\mathbf{k}}). \end{align*}\]

Then we find

\[\begin{align*} iG_{\alpha\beta}^0(\vb{x},t;\vb{x}',t') &= \begin{aligned}[t] &\theta(t-t')\frac{\delta_{\alpha\beta}}{V} \sum_{\mathbf{k}}\e^{i\mathbf{k}\cdot(\mathbf{x}-\mathbf{x}')}\e^{-i\omega_{\mathbf{k}}(t-t')}\theta(\abs{\mathbf{k}}-k_F)\\[.2cm] -{} &{}\theta(t-t') \frac{\delta_{\alpha\beta}}{V} \sum_{\mathbf{k}}\e^{i\mathbf{k}\cdot(\mathbf{x}-\mathbf{x}')} \e^{-i\omega_\mathbf{k}(t-t')}\theta(k_F-\abs{\mathbf{k}}). \end{aligned} \end{align*}\]

Single-particle Green's function for free fermions

Thus we finally obtain the single-particle Green’s function for free fermions

\[\begin{equation} \begin{split} iG_{\alpha\beta}^0(\vb{x},t;\vb{x}',t')&= \frac{\delta_{\alpha\beta}}{V} \sum_{\mathbf{k}}\qty[\theta(t-t')\theta(\abs{\mathbf{k}}-k_F)-\theta(t'-t)\theta(k_F-\abs{\mathbf{k}})] \e^{i\mathbf{k}\cdot(\mathbf{x}-\mathbf{x}')} \e^{-i\omega_{\vb{k}} (t-t')}\\[.2cm] &= \delta_{\alpha\beta} \int \frac{\dd[3]{k}}{(2\pi)^3} \qty[\theta(t-t')\theta(\abs{\mathbf{k}}-k_F)-\theta(t'-t)\theta(k_F-\abs{\mathbf{k}})]\e^{i\mathbf{k}\cdot(\mathbf{x}-\mathbf{x}')} \e^{-i\omega_{\mathbf{k}}(t-t')}. \end{split} \label{Green function} \end{equation}\]

The Fourier transform of Green’s function is

\[\begin{equation} G_{\alpha\beta}^0(\mathbf{k},\omega) = \delta_{\alpha\beta}\qty[\frac{\theta(|\mathbf{k}|-k_F)}{\omega-\omega_{\mathbf{k}} + i\eta} + \frac{\theta(k_F- |\mathbf{k}|)}{\omega-\omega_{\mathbf{k}}-i\eta}]= \delta_{\alpha\beta} \frac{1}{\omega-\omega_{\mathbf{k}} + i\ \mathrm{sgn}(\abs{\mathbf{k}}-k_F)}. \end{equation}\]

Proof

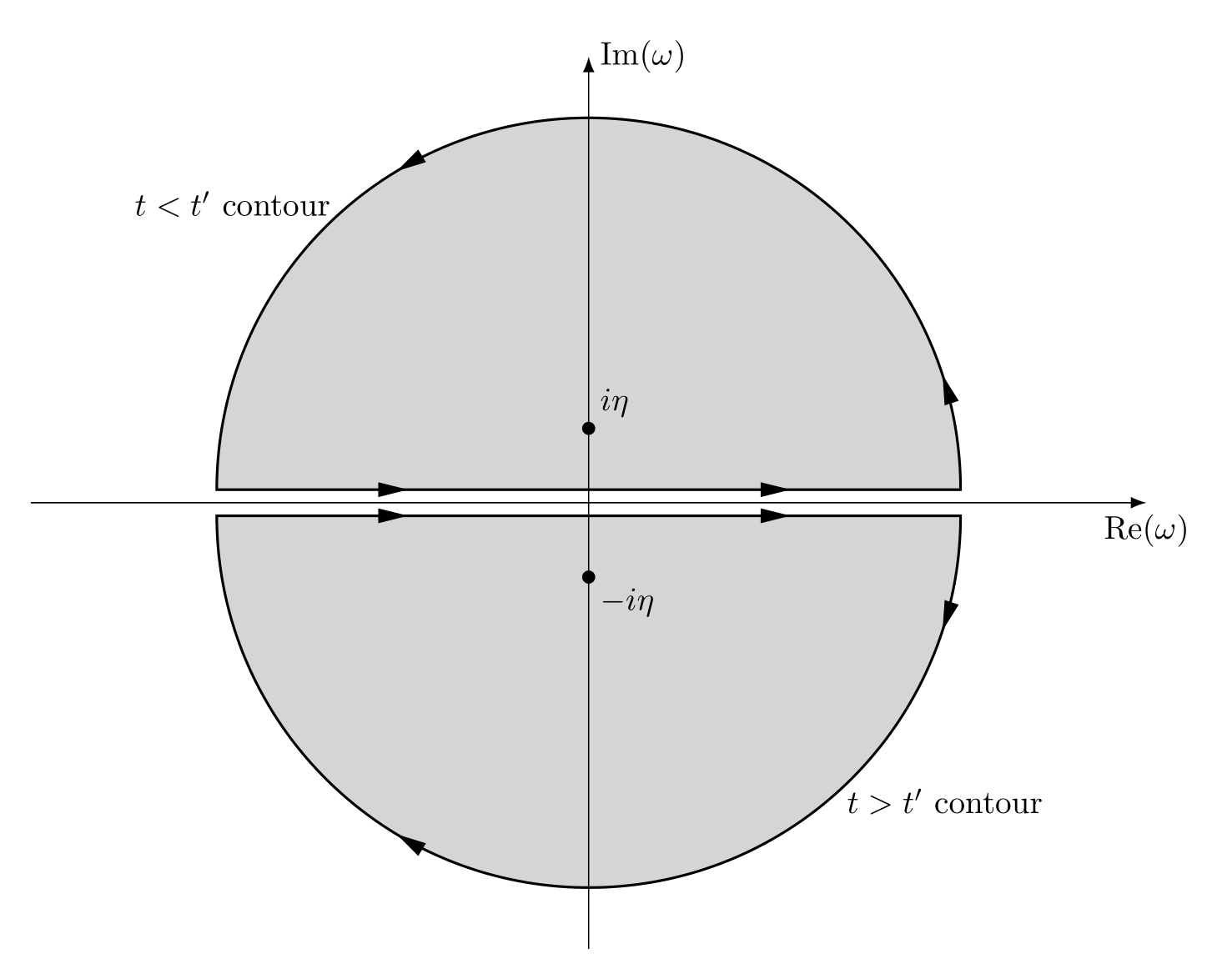
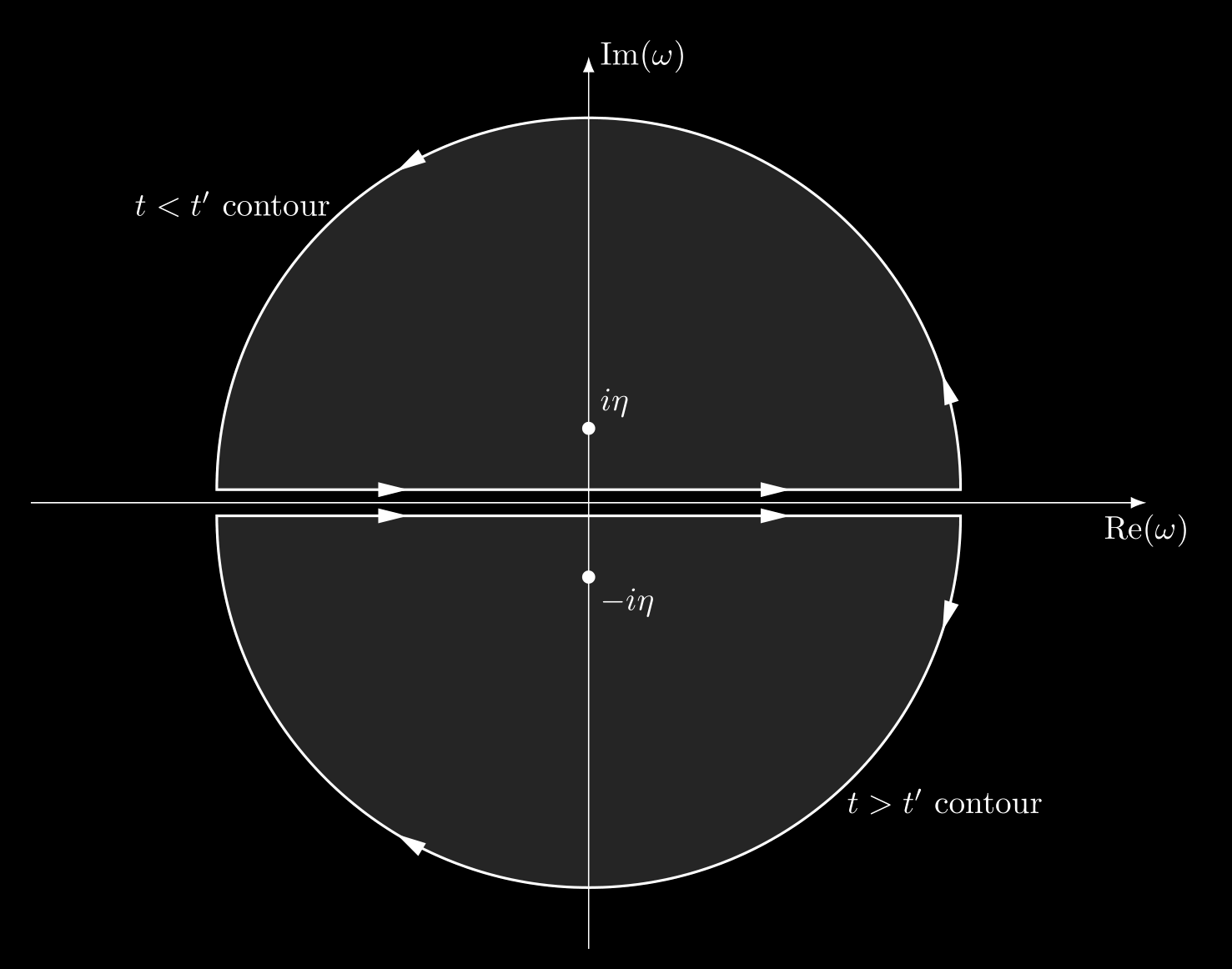
We can use an integral representation for the step function

\[\theta(t-t') = - \int_{-\infty}^{\infty} \frac{\dd{\omega}}{2\pi i } \frac{\e^{-i\omega(t-t')}}{\omega+i\eta}.\]

If $t>t’$, we choose the lower-half $\omega$ plane. If $t<t’$, we choose the upper-half $\omega$ plane.

Contour for the step function.

TikZ code

\documentclass[border=10pt]{standalone}
\usepackage{tikz}
\usetikzlibrary{arrows.meta,decorations.markings,calc,bending,shadows}

\begin{document}

\begin{tikzpicture}[>={Kite[inset=0pt,length=0.32cm,bend]},
    decoration={markings,
    mark= at position .1 with {\arrow{>}},
    mark= at position .3 with {\arrow{>}},
    mark= at position .45 with {\arrow{>}},
    mark= at position 0.8 with {\arrow{>}},
    }]
    \def\radius{4}
\filldraw[yshift=-4pt,postaction ={decorate}, thick,fill=gray!40] 
    (-\radius,0) -- (\radius,0) arc (0:-180:\radius) --cycle;

\filldraw[yshift=4pt,thick,postaction={decorate}, fill=gray!40] 
    (-\radius,0)--(\radius,0) arc (0:180:\radius)--cycle;
    
\fill (0,0.8) node[above right]{$i\eta$}  circle (2pt) ;
\fill (0,-0.8) node[below right]{$-i\eta$}  circle (2pt) ;
\node  at (140:\radius+1) {$t<t'$ contour};
\node at (-40:\radius+1) {$t>t'$ contour};

\draw[-Latex] (-\radius*1.5,0) -- (\radius*1.5,0) node[below]{$\mathrm{Re}(\omega)$};
\draw[-Latex] (0,-\radius*1.2) -- (0,\radius*1.2)node[right]{$\mathrm{Im}(\omega)$} ;
\end{tikzpicture}

\end{document}

So the Green’s function in $\eqref{Green function}$ can be rewritten as

\[G_{\alpha\beta}^0 (\vb{x},t;\vb{x}',t') = \int \frac{\dd[3]{k}\dd{\omega}}{(2\pi)^4} \e^{i\mathbf{k}\cdot(\mathbf{x}-\mathbf{x}')}\e^{-i\omega (t-t')} \times \delta_{\alpha\beta}\qty[\frac{\theta(|\mathbf{k}|-k_F)}{\omega-\omega_{\mathbf{k}} + i\eta} + \frac{\theta(k_F- |\mathbf{k}|)}{\omega-\omega_{\mathbf{k}}-i\eta}],\]

which immediately yields

\[G_{\alpha\beta}^0(\mathbf{k},\omega) = \delta_{\alpha\beta}\qty[\frac{\theta(|\mathbf{k}|-k_F)}{\omega-\omega_{\mathbf{k}} + i\eta} + \frac{\theta(k_F- |\mathbf{k}|)}{\omega-\omega_{\mathbf{k}}-i\eta}].\]

∎

And the ground state energy can be calculated via $\eqref{ground state energy}$

\[\begin{align*} E_g^0 &= - \frac{i}{2} \sum_{\alpha}\int \dd[3]{x} \lim_{\substack{\mathbf{x}'\to\mathbf{x}\\ t'\to t^+}} \qty(i\hbar \pdv{t} - \frac{\hbar^2 \nabla^2}{2m}) G_{\alpha\alpha}^0(\mathbf{x},t;\mathbf{x}',t')\\[.2cm] &=- \frac{i}{2} \sum_{\alpha}\int \dd[3]{x} \lim_{\substack{\mathbf{x}'\to\mathbf{x}\\ t'\to t^+}} \qty(i\hbar \pdv{t} - \frac{\hbar^2 \nabla^2}{2m}) \qty{ - \frac{i}{V} \sum_{\mathbf{k}}\qty[\theta(t-t')\theta(\abs{\mathbf{k}}-k_F)-\theta(t'-t)\theta(k_F-\abs{\mathbf{k}})] \e^{i\mathbf{k}\cdot(\mathbf{x}-\mathbf{x}')} \e^{-i\omega_{\vb{k}} (t-t')} }\\[.2cm] &=- \frac{i}{2} \sum_{\alpha}\int \dd[3]{x} \lim_{\substack{\mathbf{x}'\to\mathbf{x}\\ t'\to t^+}} \frac{-i}{V} \sum_{\mathbf{k}}\qty[\theta(t-t')\theta(\abs{\mathbf{k}}-k_F)-\theta(t'-t)\theta(k_F-\abs{\mathbf{k}})] \qty(\epsilon_{\mathbf{k}}^0 + \frac{\hbar^2k^2}{2m}) \e^{i\mathbf{k}\cdot(\mathbf{x}-\mathbf{x}')} \e^{-i\omega_{\vb{k}} (t-t')}\\[.2cm] &=\frac{1}{2}\sum_{\alpha}\sum_{\mathbf{k}}\theta(k_F-\abs{\mathbf{k}})(2\epsilon_\mathbf{k}^0)\\[.2cm] &=\sum_{\alpha}\sum_{\mathbf{k}}\theta(k_F-\abs{\mathbf{k}}) \epsilon_{\mathbf{k}}^0, \end{align*}\]

which is the same as $\eqref{ground state energy for free fermions}$. Of course we can use another expression $\eqref{ground state energy in k}$, then

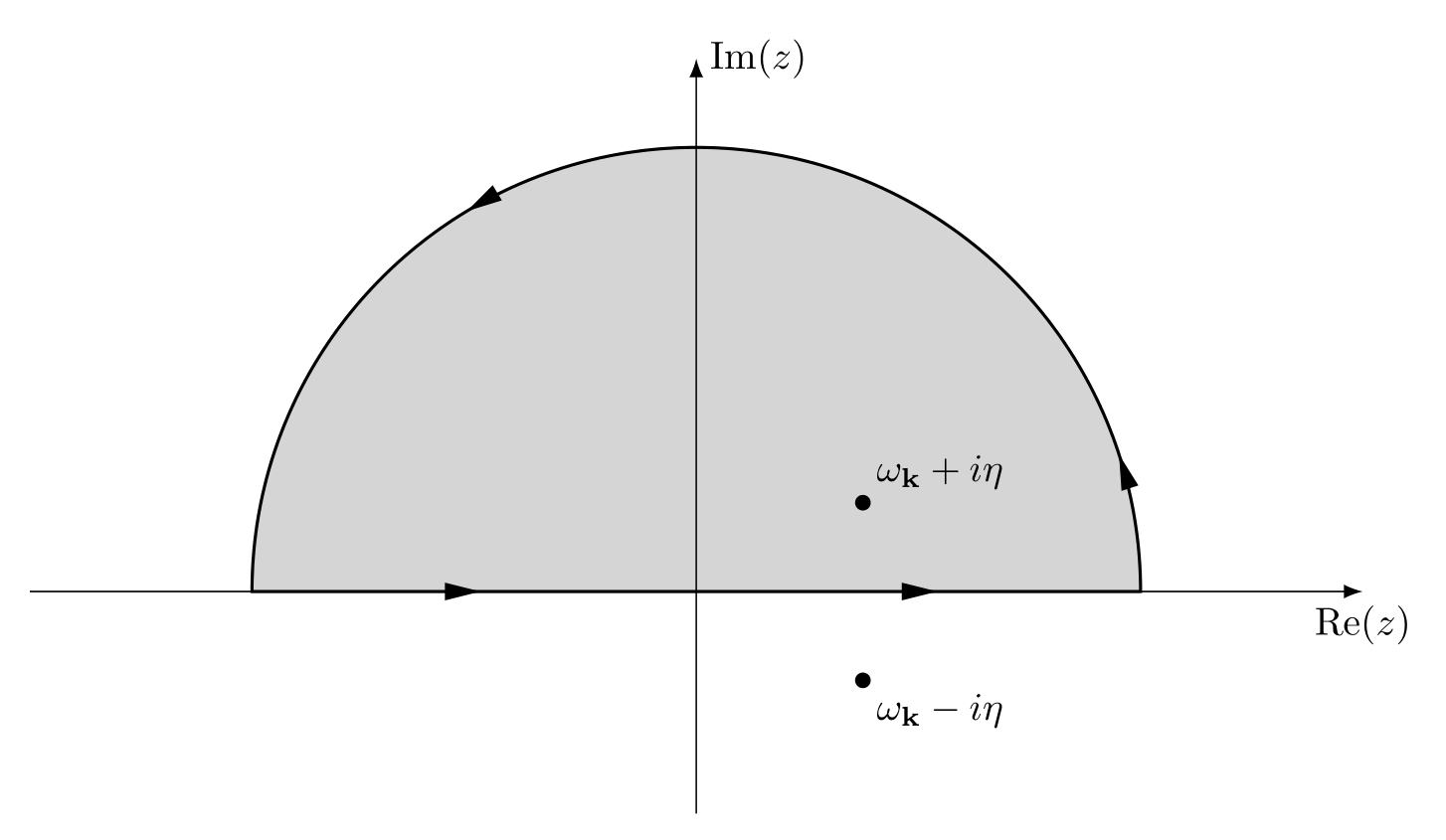
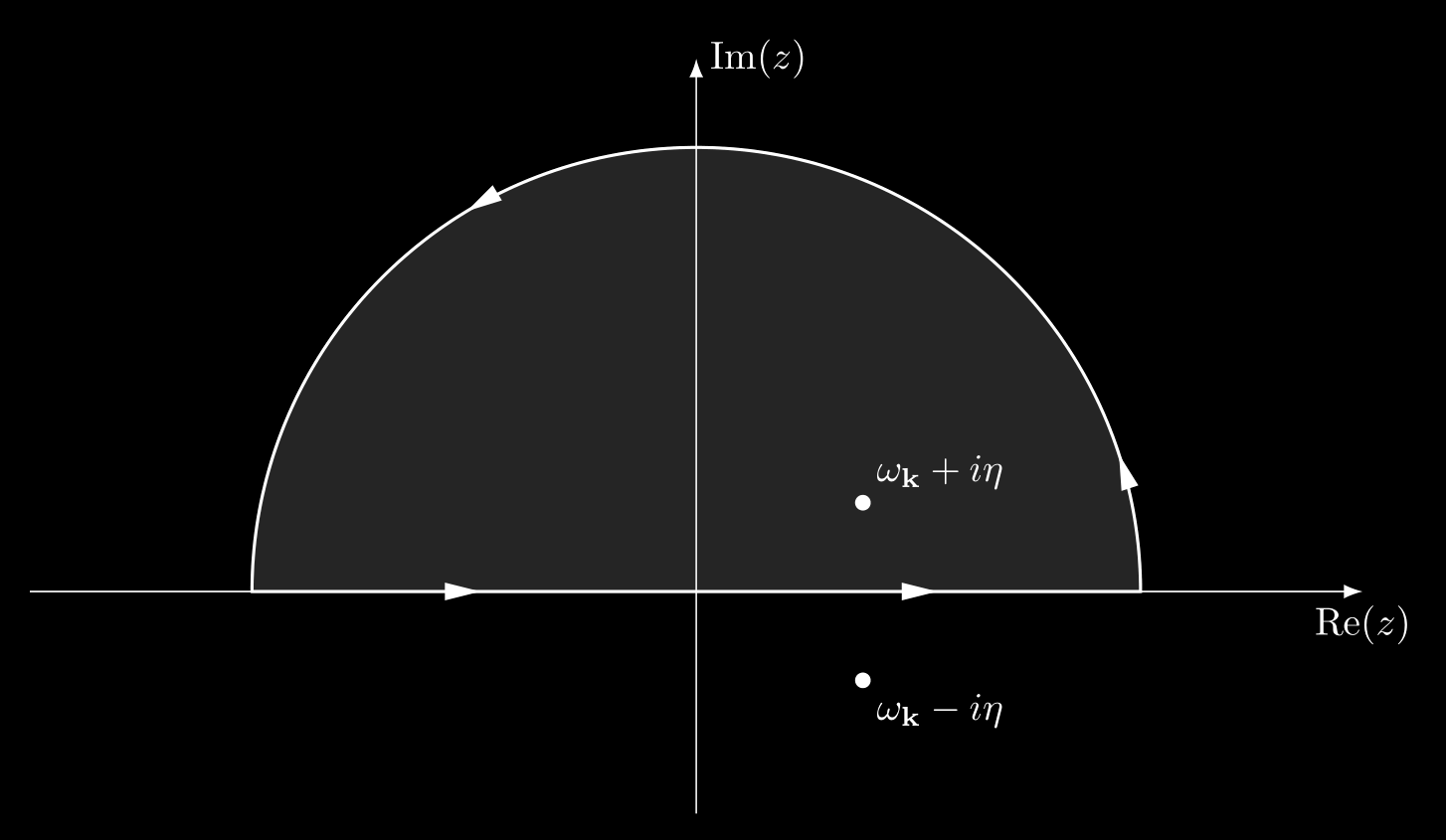
\[\begin{align*} E_g & = - \frac{i}{2}\lim_{\eta\to 0^+}\sum_{\alpha}\sum_{\vb{k}}\int_{-\infty}^{\infty} \frac{\dd{\omega}}{2\pi} \qty(\hbar\omega + \frac{\hbar^2k^2}{2m}) G_{\alpha\alpha}(\vb{k},\omega)\e^{i\omega\eta}\\[.2cm] &= - \frac{i}{2} \lim_{\eta\to 0^+}\sum_{\alpha}\sum_{\vb{k}}\int_{-\infty}^{\infty} \frac{\dd{\omega}}{2\pi} \qty(\hbar\omega + \frac{\hbar^2k^2}{2m}) \qty[\frac{\theta(|\mathbf{k}|-k_F)}{\omega-\omega_{\mathbf{k}} + i\eta} + \frac{\theta(k_F- |\mathbf{k}|)}{\omega-\omega_{\mathbf{k}}-i\eta}] \e^{i\omega \eta}\\[.2cm] &=-\frac{i}{2}\sum_{\alpha}\sum_{\mathbf{k}}\lim_{\eta\to 0^+} \oint \frac{\dd{z}}{2\pi} \qty(\hbar z + \frac{\hbar k^2}{2m}) \qty[\frac{\theta(|\mathbf{k}|-k_F)}{z-\omega_{\mathbf{k}} + i\eta} + \frac{\theta(k_F- |\mathbf{k}|)}{z-\omega_{\mathbf{k}}-i\eta}] \e^{iz \eta}\\[.2cm] & = -\frac{i}{2}\sum_{\alpha}\sum_{\mathbf{k}}\lim_{\eta\to 0^+} \frac{1}{2\pi} 2\pi i \qty(\epsilon_{\mathbf{k}}^0 + i\hbar\eta + \frac{\hbar^2 k^2}{2m}) \theta(k_F - \abs{\mathbf{k}}) \e^{i(\omega_{\mathbf{k}}+i\eta)\eta}\\[.2cm] & = \sum_{\alpha}\sum_{\mathbf{k}} \epsilon_{\mathbf{k}}^ 0 \theta(k_F - \abs{\mathbf{k}}), \end{align*}\]

where we choose the upper-half $z$ plane in third line.

Contour for the third line integral.

TikZ code

\documentclass[border=10pt]{standalone}
\usepackage{tikz}
\usetikzlibrary{arrows.meta,decorations.markings,calc,bending,shadows}

\begin{document}

\begin{tikzpicture}[>={Kite[inset=0pt,length=0.32cm,bend]},
    decoration={markings,
    mark= at position .1 with {\arrow{>}},
    mark= at position .3 with {\arrow{>}},
    mark= at position .45 with {\arrow{>}},
    mark= at position 0.8 with {\arrow{>}},
    }]
    \def\radius{4}

\filldraw[thick,postaction={decorate}, fill=gray!40] 
    (-\radius,0)--(\radius,0) arc (0:180:\radius)--cycle;
    
\fill (1.5,0.8) node[above right]{$\epsilon_{\mathbf{k}} +i\eta$}  circle (2pt) ;
\fill (1.5,-0.8) node[below right]{$\epsilon_{\mathbf{k}} +i\eta$}  circle (2pt) ;

\draw[-Latex] (-\radius*1.5,0) -- (\radius*1.5,0) node[below]{$\mathrm{Re}(z)$};
\draw[-Latex] (0,-\radius*0.5) -- (0,\radius*1.2)node[right]{$\mathrm{Im}(z)$} ;
\end{tikzpicture}

\end{document}

This result is also the same as $\eqref{ground state energy for free fermions}$.

4. References

1. Fetter, A. L., Walecka, J. D. Quantum Theory of Many-Particle Systems. Courier Corporation (2002).
2. Mahan, G. D., Many-Particle Physics. Springer Science+Business Media, LLC. (2000).
3. Altland, A., Simons, B. D., Condensed Matter Field Theory. Cambridge University Press. (2010)
4. 金彪. 量子多体理论. 2024年春