An Integral with Log

Question:

Try to solve the following integral:

\[\int_0^1 \frac{x \ln(1+x)}{1+x^4} \, \mathrm{d}x.\]

I have answered this question on Zhihu, you can find it here.

Solution:

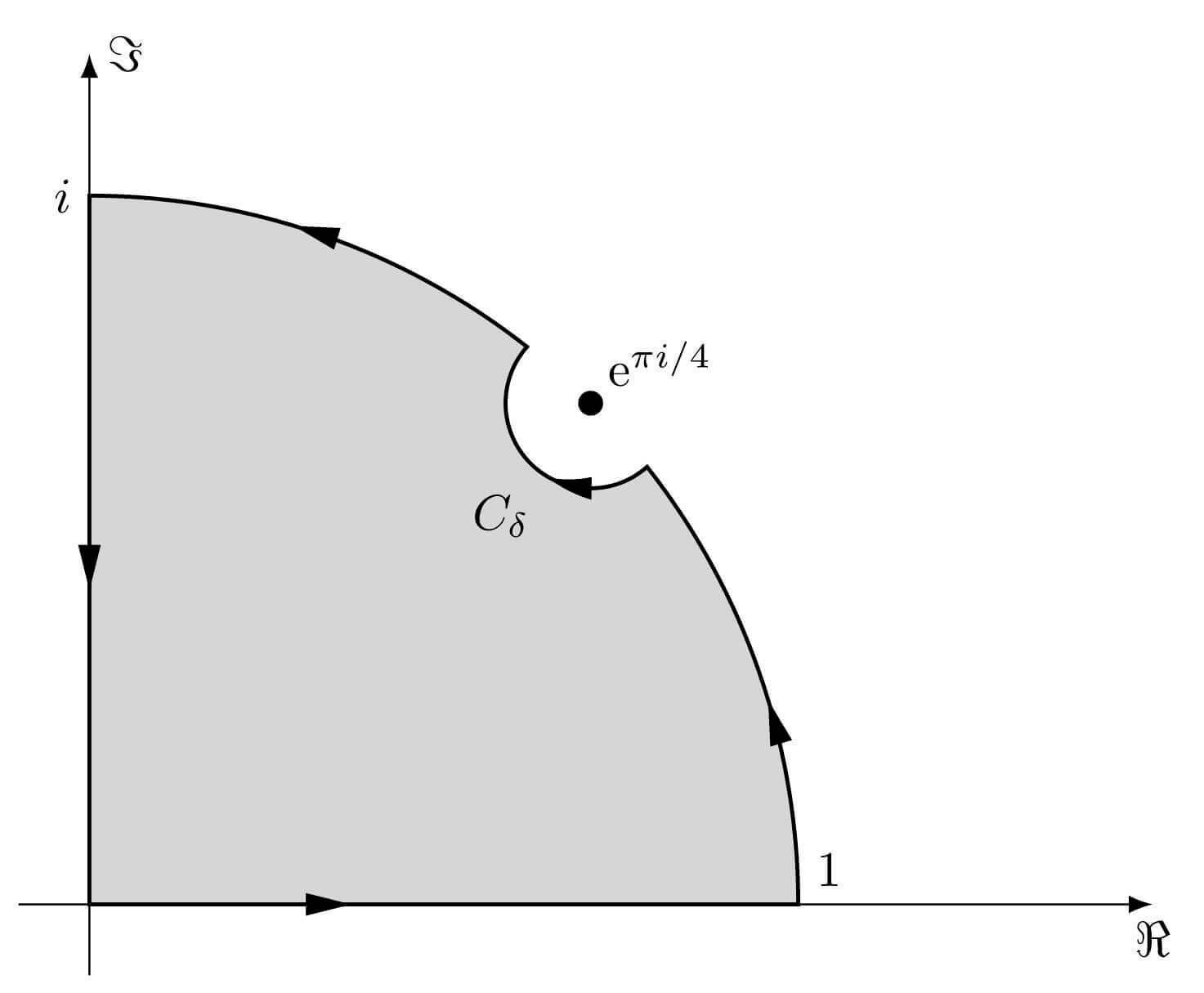
We define $ f(z) = z \ln(1+z)/(1+z^4) $ firstly, and choose the following quarter-circle contour:

Note that $ z = \mathrm{e}^{\pi i/4}$ is a singularity. Since there are no singularities within the contour, we can know from Cauchy’s theorem that:

\[\begin{aligned} &\oint_{C} f(z)\,\mathrm{d}z\\[.3cm] ={}&\int_0^{1} f(z)\, \mathrm{d}z + \left( \int_0^{\frac{\pi}{4} - \delta} + \int_{\frac{\pi}{4}+\delta}^{\frac{\pi}{2}}\right)f(\mathrm{e}^{i\theta})i \mathrm{e}^{i\theta} \, \mathrm{d}\theta + \int_{C_{\delta}} f(z) \, \mathrm{d}z + \int_i^{0} f(z)\, \mathrm{d}z\\[.3cm] ={}&0. \end{aligned}\]

The first part is what we need exactly. Since it is a real integral, so we only need take account of the real part of the other integral.

The second part can be rewritten as:

\[\begin{aligned} & \mathrm{Re}\left(\int_0^{\frac{\pi}{4}-\delta} + \int_{\frac{\pi}{4}+\delta}^{\frac{\pi}{2}} \right)f(\mathrm{e}^{i\theta}) i \mathrm{e}^{i\theta}\,\mathrm{d}\theta\\[.3cm] ={}& \mathrm{Re} \left( \int_0^{\frac{\pi}{4}-\delta} + \int_{\frac{\pi}{4}+\delta}^{\frac{\pi}{2}}\right) \frac{i\mathrm{e}^{2i\theta}}{1+\mathrm{e}^{4i\theta}} \ln(1+\mathrm{e}^{i\theta}) \, \mathrm{d}\theta\\[.3cm] ={}& \left( \int_0^{\frac{\pi}{4}-\delta} + \int_{\frac{\pi}{4}+\delta}^{\frac{\pi}{2}}\right) \frac{-1}{2\cos 2\theta} \arctan \frac{\sin\theta}{1+\cos\theta} \, \mathrm{d}\theta\\[.3cm] ={}& \left( \int_0^{\frac{\pi}{4}-\delta} + \int_{\frac{\pi}{4}+\delta}^{\frac{\pi}{2}}\right) \frac{-1}{4} \frac{\theta}{\cos 2\theta}\, \mathrm{d}\theta\\[.3cm] ={}& -\frac{1}{4} \mathrm{P.V.} \int_0^{\frac{\pi}{2}} \frac{\theta}{\cos 2\theta}\, \mathrm{d}\theta\\[.3cm] ={}& \frac{\mathbf{G}}{4}, \end{aligned}\]

where $\mathbf{G}$ is the Catalan’s constant, or you can rewrite it as:

\[\mathrm{P.V.} \int_0^{\frac{\pi}{2}} \frac{\theta}{\cos 2\theta}\, \mathrm{d}\theta = \int_0^{\frac{\pi}{4}} \frac{2\theta-\pi/2}{\cos 2\theta}\,\mathrm{d}\theta = -\frac{1}{2} \int_0^{\frac{\pi}{2}} \frac{\theta}{\sin\theta}\, \mathrm{d}\theta = -\mathbf{G}.\]

The third part is:

\[\mathrm{Re}\int_{C_{\delta}} f(z)\, \mathrm{d}z = \mathrm{Re}\left[-\pi i \cdot \mathrm{Res}\, f(\mathrm{e}^{\pi i/4})\right] = -\frac{\pi}{8} \ln (2+\sqrt{2}).\]

The fourth part can be simplified to

\[\begin{aligned} \mathrm{Re} \int_i^0 \frac{z\ln(1+z)}{1+z^4}\, \mathrm{d}z & = \mathrm{Re} \int_0^1 \frac{x\ln(1+i x)}{1+x^4}\, \mathrm{d}x\\[.5cm] & = \frac{1}{2} \int_0^{1}\frac{x\ln(1+x^2)}{1+x^4}\, \mathrm{d}x\\[.5cm] & = \frac{1}{4} \color{MediumBlue}{\int_0^{1} \frac{\ln(1+x)}{1+x^2}\, \mathrm{d}x} \\[.5cm] & = \frac{1}{4} \cdot {\color{MediumBlue}\frac{\pi \ln 2}{8}} = \frac{\pi \ln 2}{32}. \end{aligned}\]

The blue part is a well-known result.

By combining all the previous results, we can immediately obtain the original integral result as:

\[\color{red}{ \int_0^{1} \frac{x\ln(1+x)}{1+x^4}\, \mathrm{d}x = -\frac{\mathbf{G}}{4} + \frac{\pi}{8}\ln (2+\sqrt{2}) - \frac{\pi \ln 2}{32}. }\]