An Integral Involving Logarithm of Cos

Question:

Try to solve the following integral:

\[\int_0^{\frac{\pi}{2}} \frac{\ln\cos x}{x^2 + \ln^2 \cos x}\, \mathrm{d}x.\]

This question has been solved on Zhihu, you can find my solution here.

Solution:

First of all, note that $\ln (1-i\tan x) = -\ln \cos x -ix$, then we have:

\[\frac{\ln\cos x}{x^2 + \ln^2 \cos x} = - \mathrm{Re}\, \frac{1}{\ln(1-i\tan x)}.\]

Let $\tan x \mapsto z$, the original integral can be transformed to

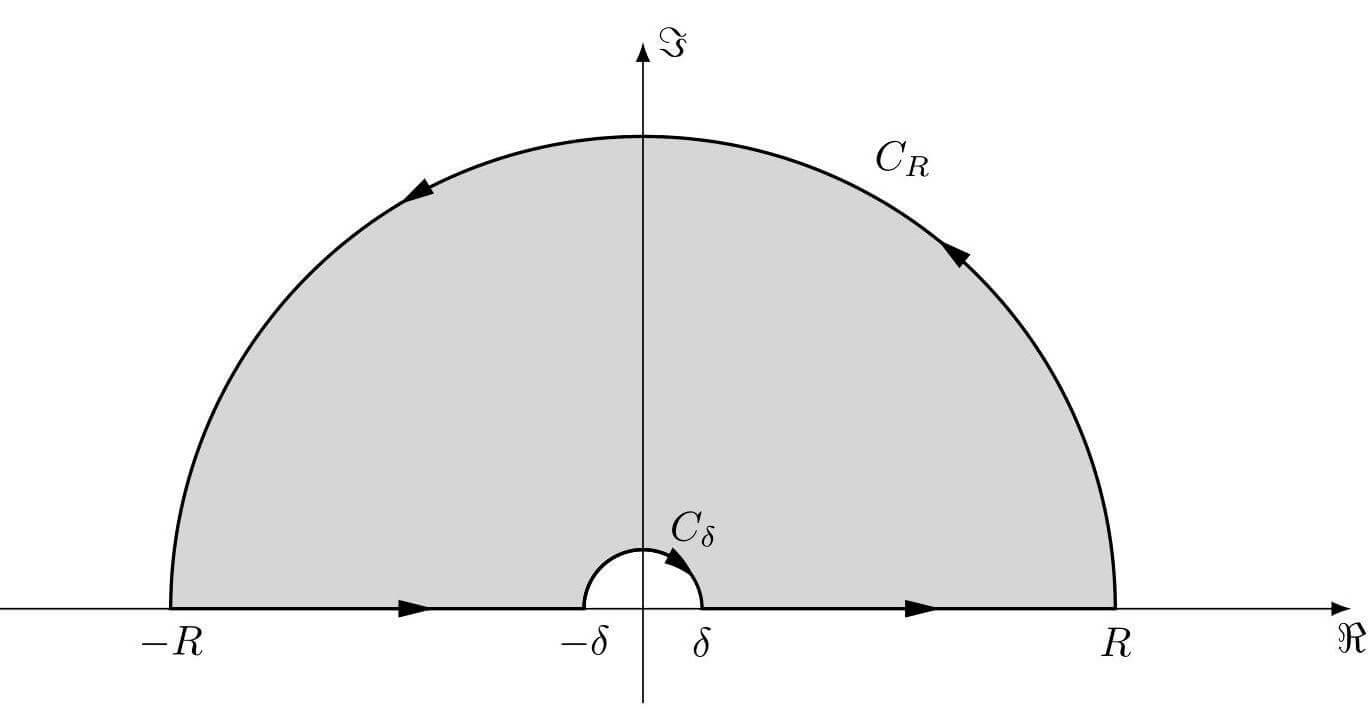
\[I = \int_0^{\frac{\pi}{2}} \frac{\ln \cos x}{x^2 + \ln^2 \cos x}\, \mathrm{d}x = \frac{1}{2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{\ln \cos x}{x^2 + \ln^2 \cos x} \, \mathrm{d}x = -\frac{1}{2} \mathrm{Re}\, \int_{-\infty}^{\infty} \frac{1}{\ln(1-iz)} \frac{\mathrm{d}z}{1+z^2}.\]

So we can define $f(z) = \dfrac{1}{\ln(1-iz)}\dfrac{1}{1+z^2}$ and use the following contour,

The branch point is $z=-i$, so $f(z)$ is single-valued and analytic in the upper half-plane. There is only one simple pole $z=i$ within the contour, and its corresponding residue is

\[\mathrm{Res}\left[\frac{1}{\ln(1-iz)} \frac{1}{1+z^2},z=i\right] = \frac{1}{2\pi \ln 2}.\]

From the residue theorem, we can obtain that

\[\left(\int_{-R}^{-\delta} + \int_{\delta}^{R}\right) f(z) \, \mathrm{d}z + \int_{C_{\delta}} f(z)\,\mathrm{d}z + \int_{C_R} f(z)\,\mathrm{d}z = 2\pi i \cdot \frac{1}{2i\ln 2} = \frac{\pi}{\ln 2}.\]

On the other hand, since we find

\[\begin{aligned} &\lim_{|z|\to 0} \frac{z}{\ln(1-iz)}\frac{1}{1+z^2} = i, \\[.5cm] &\lim_{|z|\to \infty} \frac{z}{\ln(1-iz)} \frac{1}{1+z^2} = 0. \end{aligned}\]

According to the estimation lemma, the integral over the arc can be calculated as

\[\lim_{R\to\infty} \int_{C_{R}}f(z) \, \mathrm{d}z =0,\quad \lim_{\delta\to 0} \int_{C_{\delta}}f(z)\,\mathrm{d}z = i\pi \cdot(-i) = \pi.\]

Thus,

\[\int_{-\infty}^{\infty} \frac{1}{\ln(1-iz)} \frac{\mathrm{d}z}{1+z^2} = -\pi + \frac{\pi}{\ln 2}.\]

Finally, we can immediately obtain the original integral result:

\[\color{red}{ \int_0^{\frac{\pi}{2}} \frac{\ln\cos x}{x^2 + \ln^2\cos x} \, \mathrm{d}x = \frac{\pi}{2} \left(1-\frac{1}{\ln 2} \right). }\]