§2.2 Lehmann Representation of Green's Functions (Fermions)
In this post, we discuss more analytic properties of single-particle Green’s functions. Moreover, we will derive the Lehmann representation of single-particle Green’s functions (and retarded and advanced Green’s function) in detail. Although our final expressions are formally applicable to both bosons and fermions, the existence of Bose condensation at $T=0$ introduces additional complications, and we shall consider only fermions in next posts.
1. The Lehmann representation of single-particle Green’s functions
1.1. The Lehmann representation
The Hamiltonian $\hat{H}$, total momentum operator $\hat{\mathbf{P}}$ and total particle number operator are commute with each other, so they have common eigenstates which form a complete orthonormal basis. We define a set of common eigenstates as $\qty{N,E_n(N),\mathbf{P}(N)}$ which satisfies
\[\begin{equation} \begin{cases} \displaystyle{\braket{N',E_{n'}(N'),\mathbf{P}'(N')}{N,E_n(N),\mathbf{P}(N)} = \delta_{N'N}\delta_{n'n}\delta_{\mathbf{P}'\mathbf{P}}}, \quad \text{Orthonormalization},\\[.3cm] \displaystyle{\sum_{N}\sum_{n}\sum_{\mathbf{P}} \ket{N,E_n(N),\mathbf{P}}\bra{N,E_n(N),\mathbf{P}(N)} = \mathbb{1}}, \quad \text{Completeness}, \end{cases} \end{equation}\]where $E_n(N)$ represents the $n$-th excited energy when the number of particles is $N$. We usually write $\ket{N,E_n(N),\mathbf{P}(N)}$ simply as $\ket{N,n,\mathbf{P}}$. The ground state is defined as $\ket{N_g,E_g(N_g),\mathbf{P}_g(N_g)}$, its energy is $E_{n=0}=E_g$.
Now we assume that $\hat{H}$ is time independent and the system is translational invariance (i.e. $[\hat{H},\hat{\mathbf{P}}] =0 $). Then the Green’s function can be rewritten as
\[\begin{align*} i G_{\alpha\beta}(\mathbf{x}-\mathbf{x}',t-t') &= \ev{\hat{\mathsf{T}}\qty[\hat{\psi}_{H\alpha}(\vb{x},t)\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')]}{\psi_{H}^0}\\[.2cm] &=\theta(t-t')\underbrace{\ev{\hat{\psi}_{\alpha}(0)\e^{i\hat{\mathbf{P}}\cdot(\mathbf{x}-\mathbf{x}')/\hbar}\textcolor{crimson}{\mathbb{1}}\e^{-i\hat{H}(t-t')/\hbar}\hat{\psi}_{\beta}^\dagger(0)}{\psi_H^0}}_{\mathrm{I}}\e^{iE_{g}(t-t')/\hbar}\\[.2cm] &\quad - \theta(t'-t)\underbrace{\ev{\hat{\psi}_{\beta}^\dagger(0)\e^{-i\hat{\mathbf{P}}\cdot(\mathbf{x}-\mathbf{x}')/\hbar}\textcolor{crimson}{\mathbb{1}}\e^{i\hat{H}(t-t')/\hbar}\hat{\psi}_{\alpha}^(0)}{\psi_H^0}}_{\mathrm{II}}\e^{iE_{g}(t-t')/\hbar}\\[.2cm] \end{align*}\]where we have used derivation results in the previous section and $\hat{\mathbf{P}}\ket{\psi_H^0} =0$ in second equal. Then we find
\[\begin{align} \mathrm{I}& = \sum_{n,\mathbf{P}} \mel{\psi_H^0}{\hat{\psi}_\alpha(0)}{N_{g}+1,n,\mathbf{P}}\mel{N_{g}+1,n,\mathbf{P}}{\hat{\psi}_{\beta}^\dagger(0)}{\psi_H^0}\e^{i\mathbf{P}\cdot(\mathbf{x}-\mathbf{x}')/\hbar}\e^{-iE_n(N_g+1)(t-t')/\hbar},\\[.2cm] \mathrm{II}& = \sum_{n,\mathbf{P}} \mel{\psi_H^0}{\hat{\psi}_{\beta}^\dagger(0)}{N_g-1,n,\mathbf{P}}\mel{N_g-1,n,\vb{P}}{\hat{\psi}_{\alpha}(0)}{\psi_H^0}\e^{-i\vb{P}\cdot(\vb{x}-\vb{x}')/\hbar}\e^{iE_n(N_g-1)(t-t')/\hbar}. \end{align}\]Proof
Let’s take $\mathrm{I}$ as an example to calculate the result,
\[\begin{align*} \mathrm{I}& =\ev{\hat{\psi}_{\alpha}(0)\e^{i\hat{\mathbf{P}}\cdot(\mathbf{x}-\mathbf{x}')/\hbar}\textcolor{crimson}{\mathbb{1}}\e^{-i\hat{H}(t-t')/\hbar}\hat{\psi}_{\beta}^\dagger(0)}{\psi_H^0}\\[.2cm] &= \textcolor{crimson}{\sum_{N,n,\vb{P}}} \bra{\psi_H^0}\hat{\psi}_{\alpha}(0)\e^{i\hat{\vb{P}}\cdot(\vb{x}-\vb{x}')/\hbar}\textcolor{crimson}{\ket{N,n,\vb{P}}\bra{N,n,\vb{P}}}\e^{-i\hat{H}(t-t')/\hbar}\hat{\psi}_{\beta}^\dagger(0)\ket{\psi_H^0}\\[.2cm] &=\sum_{N,n,\vb{P}}\mel{\psi_H^0}{\hat{\psi}_{\alpha}(0)}{N,n,\vb{P}} \mel{N,n,\vb{P}}{\hat{\psi}_{\beta}^\dagger(0)}{\psi_{H}^0}\e^{i\vb{P}\cdot(\vb{x}-\vb{x}')/\hbar} \e^{-iE_n(N)(t-t')/\hbar}. \end{align*}\]Note that $\hat{N}\hat{\psi}_{\beta}^\dagger(0)\ket{\psi_H^0} = (N_{g}+1) \hat{\psi}_{\beta}(0)^\dagger\ket{\psi_H^0}$, so $N$ must equal to $N_{g}+1$ in the above sum,
\[\mathrm{I} = \sum_{n,\mathbf{P}} \mel{\psi_H^0}{\hat{\psi}_\alpha(0)}{N_{g}+1,n,\mathbf{P}}\mel{N_{g}+1,n,\mathbf{P}}{\hat{\psi}_{\beta}^\dagger(0)}{\psi_H^0}\e^{i\mathbf{P}\cdot(\mathbf{x}-\mathbf{x}')/\hbar}\e^{-iE_n(N_g+1)(t-t')/\hbar}.\]This is exactly the desired result and the same method can be used for $\mathrm{II}$.
∎
For simplicity, we introduce two weight functions $A_{\alpha\beta}(n,\vb{P})$ and $B_{\alpha\beta}(n,\vb{P})$:
\[\begin{align} A_{\alpha\beta}(n,\vb{P})&:= \mel{\psi_H^0}{\hat{\psi}_\alpha(0)}{N_{g}+1,n,\mathbf{P}}\mel{N_{g}+1,n,\mathbf{P}}{\hat{\psi}_{\beta}^\dagger(0)}{\psi_H^0},\label{weight function A} \\[.2cm] B_{\alpha\beta}(n,\vb{P})&:= \mel{\psi_H^0}{\hat{\psi}_{\beta}^\dagger(0)}{N_g-1,n,\mathbf{P}}\mel{N_g-1,n,\vb{P}}{\hat{\psi}_{\alpha}(0)}{\psi_H^0}. \label{weight function B} \end{align}\]then
\[\begin{equation} \begin{split} G_{\alpha\beta}(\vb{x}-\vb{x}',t-t') =& -i \sum_{n,\vb{P}} \theta(t-t') A_{\alpha\beta}(n,\vb{P}) \e^{i\vb{P}\cdot(\vb{x}-\vb{x}')/\hbar} \e^{-i (E_n(N_g+1)-E_g)(t-t')/\hbar}\\[.2cm] &+i\sum_{n,\vb{P}} \theta(t'-t) B_{\alpha\beta}(n,\vb{P})\e^{-i\vb{P}\cdot(\vb{x}-\vb{x}')/\hbar}\e^{i(E_n(N_g-1)-E_g)(t-t')/\hbar}. \end{split} \end{equation}\]The corresponding Fourier transform is
\[\begin{align} G_{\alpha\beta}(\vb{k},\omega) ={}& \int \dd[3]{(x-x')}\int\dd{(t-t')} G_{\alpha\beta}(\vb{x}-\vb{x}',t-t') \e^{-i\vb{k}\cdot(\vb{x}-\vb{x}')}\e^{i\omega(t-t')}\notag\\[.2cm] ={}& V \sum_n \frac{A_{\alpha\beta}(n,\hbar\vb{k})}{\omega - \hbar^{-1}(E_n(N_g+1)- E_g(N_g))+i\eta}\notag \\[.2cm] &\quad {}+{} V \sum_n \frac{B_{\alpha\beta}(n,-\hbar\vb{k})}{\omega+ \hbar^{-1}(E_n(N_g-1)- E_g(N_g)) - i\eta}, \label{green function k space 1} \end{align}\]where the $\pm i\eta$ is necessary to ensure the convergence of the integral over $t-t’$. For simplicity, we just write $A_{\alpha\beta}(n,\hbar \vb{k})$ as $ A_{\alpha\beta}(n,\vb{k})$ and $B_{\alpha\beta}(n,-\hbar \vb{k}) $ as $ B_{\alpha\beta}(n,-\vb{k})$
Proof
This result is not obvious, the computation is omitted from the first to the second step, and here we prove it.
\[\begin{align*} G_{\alpha\beta}(\vb{k},\omega) =& \int \dd[3]{(x-x')}\int\dd{(t-t')}G_{\alpha\beta}(\vb{x}-\vb{x}',t-t') \e^{-i\vb{k}\cdot(\vb{x}-\vb{x}')}\e^{i\omega(t-t')}\\[.2cm] =&-i \sum_{n,\vb{P}} A_{\alpha\beta}(n,\vb{P})\int \dd[3]{(x-x')}\int\dd{(t-t')}\theta(t-t')\e^{i\vb{P}\cdot(\vb{x}-\vb{x}')/\hbar} \e^{-i (E_n(N_g+1)-E_g)(t-t')/\hbar}\cdot \e^{-i\vb{k}\cdot(\vb{x}-\vb{x}')}\e^{i\omega(t-t')}\\[.2cm] & +i\sum_{n,\vb{P}} B_{\alpha\beta}(n,\vb{P}) \int \dd[3]{(x-x')}\int\dd{(t-t')}\theta(t'-t)\e^{-i\vb{P}\cdot(\vb{x}-\vb{x}')/\hbar}\e^{i(E_n(N_g-1)-E_g)(t-t')/\hbar}\cdot \e^{-i\vb{k}\cdot(\vb{x}-\vb{x}')}\e^{i\omega(t-t')}\\[.2cm] =&-i V \sum_{n,\vb{P}} A_{\alpha\beta}(n,\vb{P})\delta_{\vb{k},\vb{P}/\hbar}\int\dd{(t-t')}\theta(t-t')\e^{-i (E_n(N_g+1)-E_g)(t-t')/\hbar}\e^{i\omega(t-t')}\\[.2cm] &{}+ i V \sum_{n,\vb{P}} B_{\alpha\beta}(n,\vb{P})\delta_{-\vb{k},\vb{P}/\hbar}\int\dd{(t-t')}\theta(t'-t)\e^{i (E_n(N_g-1)-E_g)(t-t')/\hbar}\e^{i\omega(t-t')}. \end{align*}\]Using the integral expression of the step function
\[\theta(t) = -\frac{1}{2\pi i} \int_{-\infty}^{\infty}\frac{\e^{-i tz}}{z+i\eta}\dd{z}, \quad \eta \to 0^+,\]we can get
\[\begin{align*} &\int_{-\infty}^{\infty}\dd{(t-t')}\theta(t-t')\e^{-i (E_n(N_g+1)-E_g)(t-t')/\hbar}\e^{i\omega(t-t')}\\[.2cm] ={}&-\frac{1}{2\pi i} \int_{-\infty}^{\infty} \frac{\dd{z}}{z+i\eta} \int_{-\infty}^{\infty}\dd{(t-t')}\exp\qty[-i\qty(z+\frac{E_n(N_g+1)-E_g}{\hbar}-\omega) (t-t')]\\[.2cm] ={}&i\int_{-\infty}^{\infty} \frac{\delta(z+\hbar^{-1}(E_n-E_g) \omega)}{z+i\eta} \dd{z} = \frac{i}{\omega-\hbar^{-1}(E_n(N_g+1)-E_g(N_g)) + i\eta}. \end{align*}\]Similarly,
\[\int_{-\infty}^{\infty}\dd{(t-t')}\theta(t'-t)\e^{i (E_n(N_g-1)-E_g)(t-t')/\hbar}\e^{i\omega(t-t')} = \frac{-i}{\omega-\hbar^{-1}(E_n(N_g-1)-E_g(N_g))-i\eta}.\]Substituting these two results into the sum, we can reach the final result.
∎
It is helpful to examine denominators in a little more detail. In the first sum the denominator may be written as
\[\omega - \frac{E_n(N_g+1) - E_g(N_g)}{\hbar} = \omega -\frac{E_n(N_g+1) - E_g(N_g+1)}{\hbar} - \frac{E_g(N_g+1) - E_g(N_g)}{\hbar}.\]Now $E_g(N_g+1) - E_g(N_g)$ is the change in ground state energy as one extra particle is added to the system. Since the volume of the system is kept constant, this change in energy is just the chemical potential. And the quantity $\epsilon_{n,\vb{k}} := E_n(N_g+1)-E_g(N_g+1)$ is the excitation energy of the $N_g+1$ particle system and $\epsilon_{n,\vb{k}}\geq 0$. So
\[\begin{equation} \omega - \frac{E_n(N_g+1) - E_g(N_g)}{\hbar} = \omega - \hbar^{-1}\epsilon_{n,\vb{k}}(N_g+1) -\hbar^{-1}\mu. \label{denominator1} \end{equation}\]Similarly,
\[\begin{equation} \omega + \frac{E_n(N_g-1) - E_g(N_g)}{\hbar} = \omega + \hbar^{-1}\epsilon_{n,-\vb{k}}(N_g-1) - \hbar^{-1}\mu. \label{denominator2} \end{equation}\]Note that the very definition of the thermodynamic limit implies $\mu(N_g+1) = \mu(N_g) + \mathcal{O}(N_{g}^{-1})$, so we can neglect the difference between them.
Equations $\eqref{denominator1}$ and $\eqref{denominator2}$ can now be combined with $\eqref{green function k space 1}$ to give the Lehmann representation of single-particle Green’s function
\[\begin{equation} \begin{split} G_{\alpha\beta}(\vb{k},\omega) ={}& \hbar V \sum_{n} \frac{A_{\alpha\beta}(n,\vb{k})}{\hbar \omega - \epsilon_{n,\mathbf{k}}(N_g+1) - \mu + i\eta} \\[.2cm] &\quad {}+{} \hbar V \sum_{n} \frac{B_{\alpha\beta}(n,-\vb{k})}{\hbar\omega + \epsilon_{n,-\vb{k}}(N_g-1) -\mu - i\eta}\\[.2cm] ={}&\hbar V \sum_{n} \frac{\mel{\psi_H^0}{\hat{\psi}_\alpha(0)}{N_{g}+1,n,\mathbf{k}}\mel{N_{g}+1,n,\mathbf{k}}{\hat{\psi}_{\beta}^\dagger(0)}{\psi_H^0}}{\hbar \omega - \epsilon_{n,\mathbf{k}}(N_g+1) - \mu + i\eta}\\[.2cm] &\quad {} + {} \hbar V \sum_{n} \frac{\mel{\psi_H^0}{\hat{\psi}_{\beta}^\dagger(0)}{N_g-1,n,-\mathbf{k}}\mel{N_g-1,n,-\vb{k}}{\hat{\psi}_{\alpha}(0)}{\psi_H^0}.}{\hbar\omega + \epsilon_{n,-\vb{k}}(N_g-1) -\mu - i\eta}, \end{split} \label{lehmann representation for G} \end{equation}\]where $A_{\alpha\beta}$ and $B_{\alpha\beta}$ are defined in $\eqref{weight function A}$ and $\eqref{weight function B}$.
1.2. Analytic properties
Now we will discuss the analytic properties of the Green’s function. The crucial observation is that the function $G_{\alpha\beta}(\vb{k},\omega)$ is a meromorphic function of $\hbar\omega$, with simple poles at the exact excitation energies of the interacting system corresponding to a momentum $\hbar\vb{k}$. For frequencies below $\mu/\hbar$, these singularities lie slightly above the real axis, and for frequencies above $\mu/\hbar$, these singularities lie slightly below the real axis.
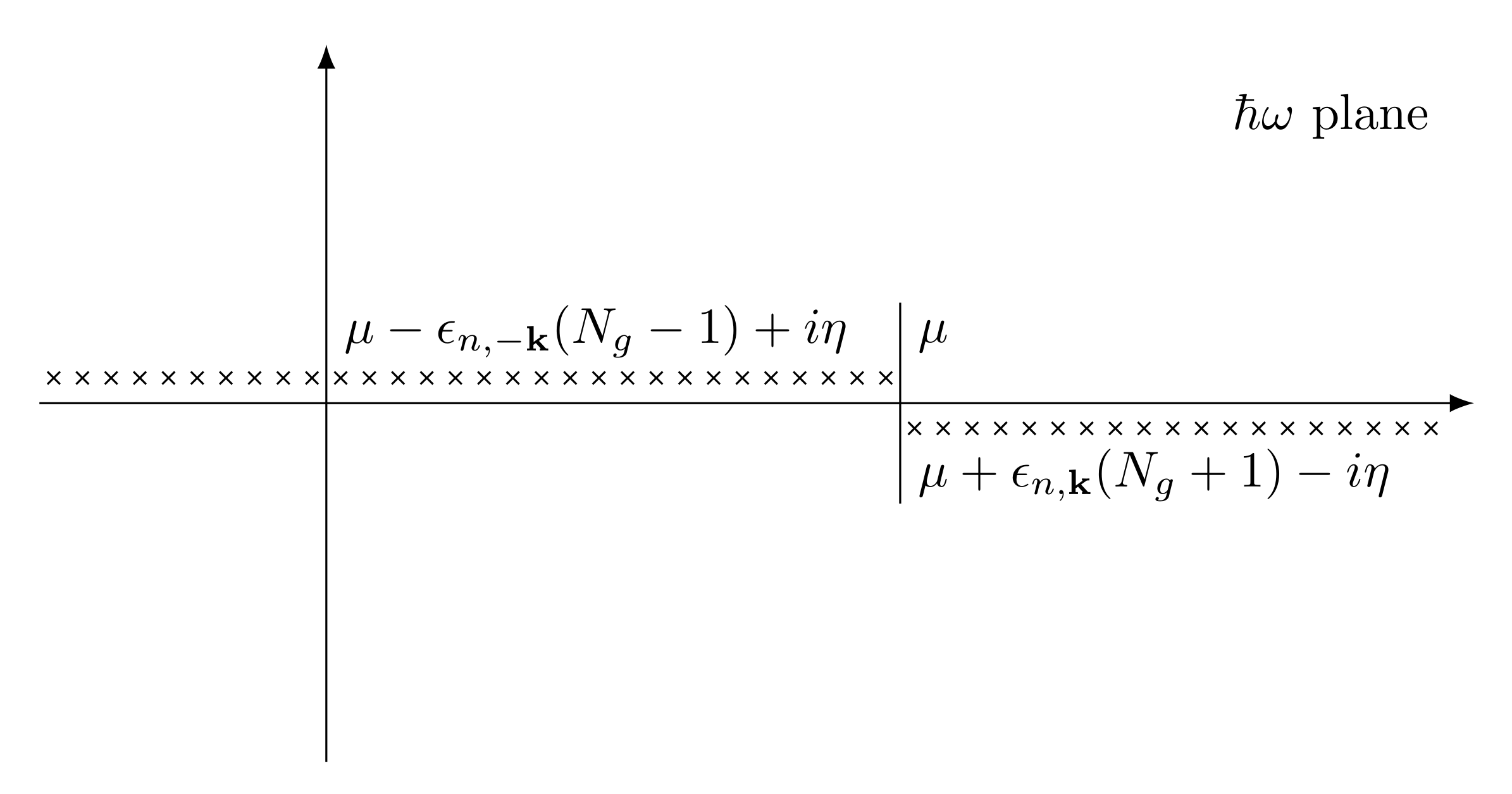
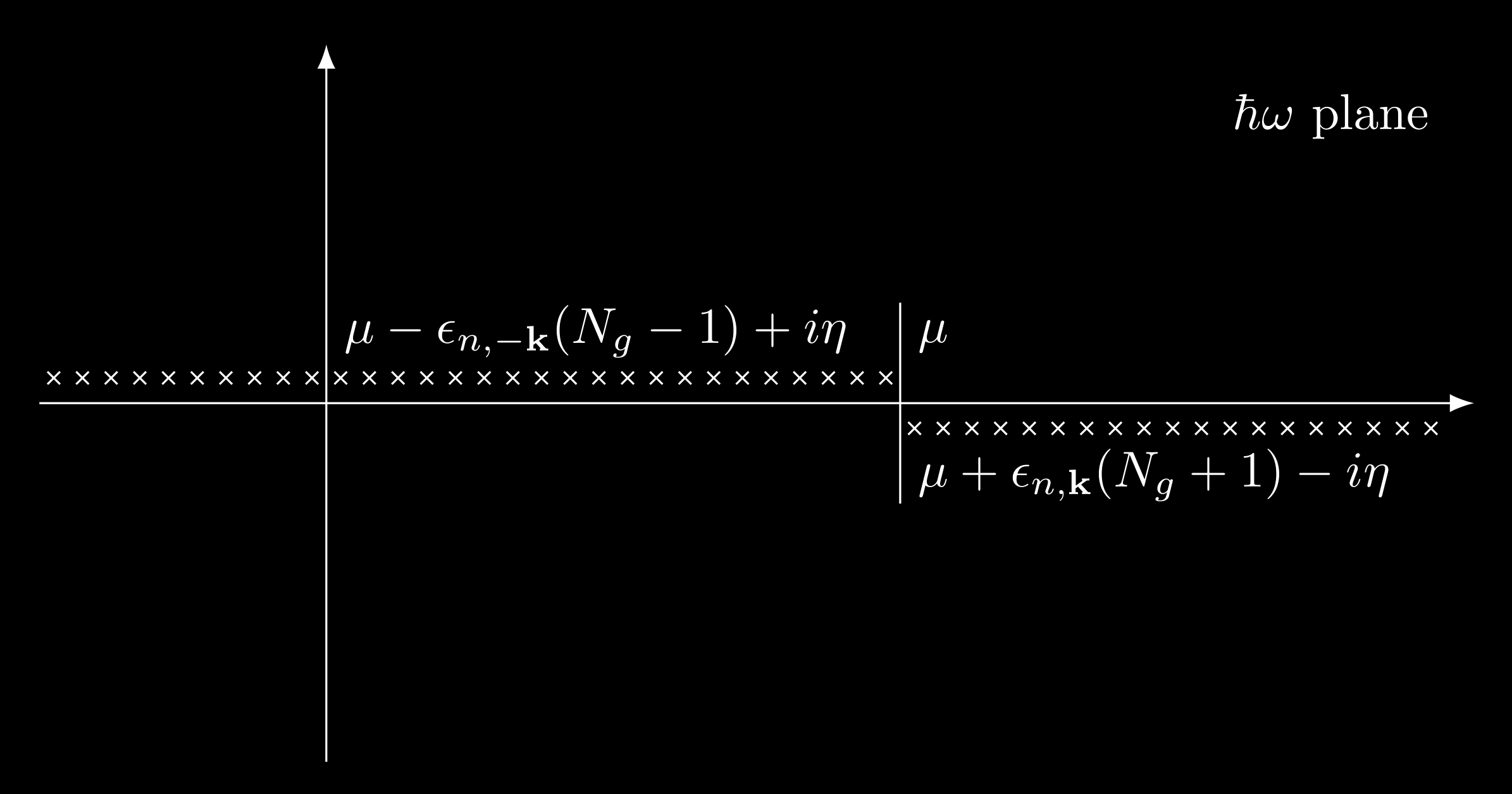
TikZ code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
\documentclass[border=10pt]{standalone}
\usepackage{tikz}
\usetikzlibrary{arrows.meta}
\usetikzlibrary{decorations.shapes}
\begin{document}
\begin{tikzpicture}
\draw[-Latex] (-2,0) -- (8,0);
\draw[-Latex] (0,-2.5) -- (0,2.5);
\draw (4,-0.7) -- (4,0.7) node[below right]{$\mu$};
\draw[yshift=5pt,decorate,decoration={crosses,segment length=0.2cm}] (-1.9,0) - - (3.9,0);
\draw[yshift=-5pt,decorate,decoration={crosses,segment length=0.2cm}] (4.1,0) - - (7.8,0);
\node at (0,0.5) [right]{$\mu - \epsilon_{n,-\mathbf{k}}(N_g-1)+i\eta$};
\node at (4,-0.5)[right]{$\mu + \epsilon_{n,\mathbf{k}}(N_g+1)-i\eta$};
\node at (7,2){$\hbar\omega$ plane};
\end{tikzpicture}
\end{document}
- For an interacting system, the field operator connects the ground state with very many excited states of the system containing $N_g\pm 1$ particles.
- For the noninteracting system, however, the field operator connects only one state to the ground state.
So $G^0(\vb{k},\omega)$ has only a single pole, slightly below the real axis at $\hbar\omega =\hbar^2k^2/2m$ if $k>k_F$ and slightly above the real axis at the same value of $\hbar\omega = \hbar^2k^2/2m$ if $k<k_F$.
So the Green’s function $G$ is analytic in neither the upper nor the lower $\omega$ plane.
2. Retard and advanced Green’s functions
2.1. Definition of retarded and advanced Green’s functions
For contour integrations, it is useful to consider functions that are analytic in one half plane or the other. We therefore define a new pair of functions, known as retarded and advanced Green’s functions.
Retarded Green’s function:
\[\begin{equation} G_{\alpha\beta}^{R}(\vb{x},t;\vb{x}',t') =-i \theta(t-t') \ev{\qty[\hat{\psi}_{H\alpha}(\vb{x},t),\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')]_+}{\psi_H^0}, \label{lehmann representation for G R} \end{equation}\]Advanced Green’ function:
\[\begin{equation} G_{\alpha\beta}^{A}(\vb{x},t;\vb{x}',t') =i \theta(t'-t) \ev{\qty[\hat{\psi}_{H\alpha}(\vb{x},t),\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')]_+}{\psi_H^0}, \label{lehmann representation for G A} \end{equation}\]
where the plus signs denote anticommutator for fermions.
In the same way we derived $\eqref{lehmann representation for G}$, we can also get the Lehmann representation of retarded and advanced Green’s functions:
In a homogeneous system, we find the Lehmann representation of $G^{R,A}$:
\[\begin{equation} \begin{split} G_{\alpha\beta}^{R,A}(\vb{k},\omega) ={}&\hbar V \sum_{n} \frac{\mel{\psi_H^0}{\hat{\psi}_\alpha(0)}{N_{g}+1,n,\mathbf{k}}\mel{N_{g}+1,n,\mathbf{k}}{\hat{\psi}_{\beta}^\dagger(0)}{\psi_H^0}}{\hbar \omega - \epsilon_{n,\mathbf{k}}(N_g+1) - \mu \pm i\eta}\\[.2cm] &\quad {} + {} \hbar V \sum_{n} \frac{\mel{\psi_H^0}{\hat{\psi}_{\beta}^\dagger(0)}{N_g-1,n,-\mathbf{k}}\mel{N_g-1,n,-\vb{k}}{\hat{\psi}_{\alpha}(0)}{\psi_H^0}.}{\hbar\omega + \epsilon_{n,-\vb{k}}(N_g-1) -\mu \pm i\eta}, \end{split} \end{equation}\]Note that $G^{R}_{\alpha\beta}(\vb{k},\omega)$ and $G^{A}_{\alpha\beta}(\vb{k},\omega)$ are again meromorphic functions of $\omega$. All the poles of $G^{R}_{\alpha\beta}(\vb{k},\omega)$ lie in the lower half plane, so that $G^{R}_{\alpha\beta}(\vb{k},\omega)$ is analytic for $\mathrm{Im}\ \omega >0$; in contrast, all the poles of $G^{A}_{\alpha\beta}(\vb{k},\omega)$ lie in the upper half plane, so that $G^{A}_{\alpha\beta}(\vb{k},\omega)$ is analytic for $\mathrm{Im}\ \omega<0$.
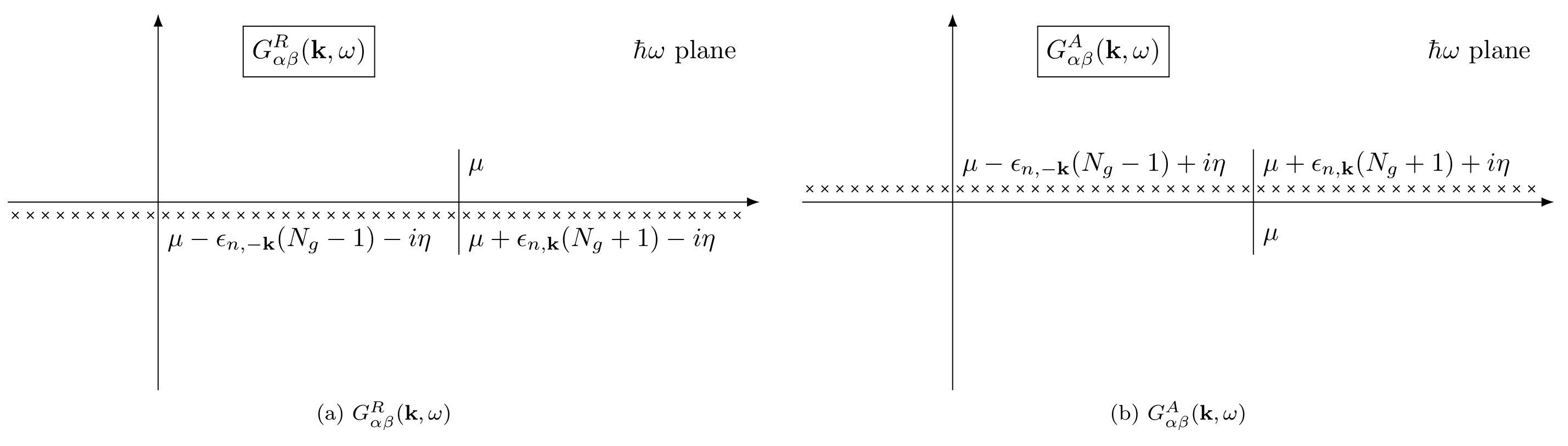
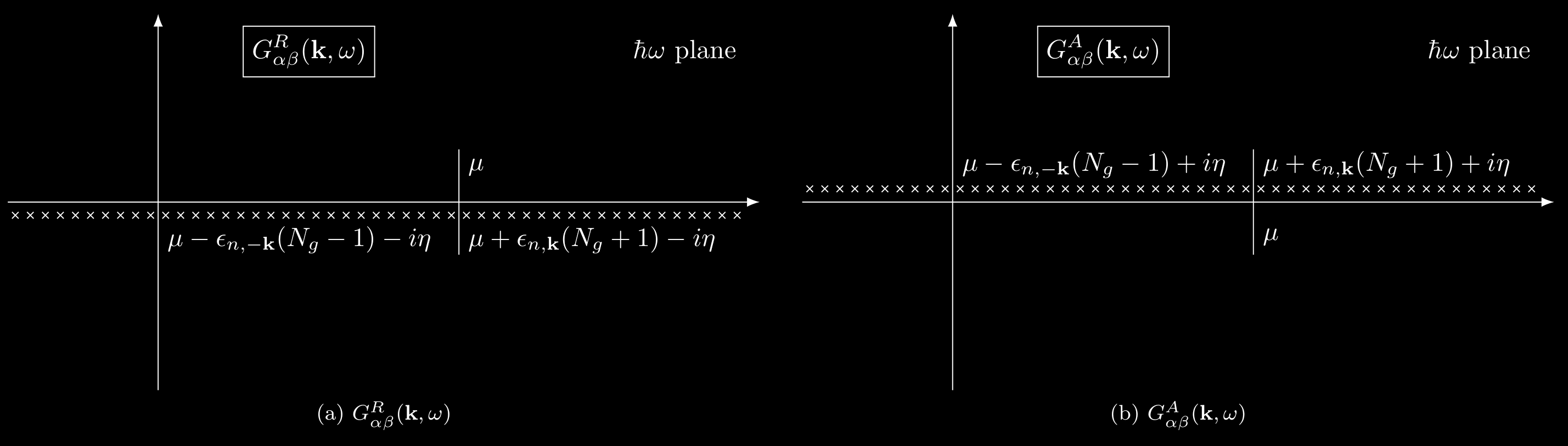
2.2. The relation between $G^{R,A}$ and $G$
For real $\omega$, we have
\[\begin{equation} [G^{R}_{\alpha\beta}(\vb{k},\omega)]^* = G_{\beta\alpha}^{A}(\vb{k},\omega). \label{relation 1} \end{equation}\]Proof
\[\begin{align*} G_{\alpha\beta}^{R*}(\vb{k},\omega) & = \hbar V \sum_{n} \frac{\mel{\psi_{H}^0}{\hat{\psi}_{\alpha}(0)}{N_g+1,n,\vb{k}}^* \mel{N_g+1,n,\vb{k}}{\hat{\psi}_{\beta}^\dagger(0)}{\psi_H^0}^*}{\hbar\omega - \mu - \epsilon_{n,\vb{k}}(N_g+1) - i\eta}\\[.2cm] &\quad {}+{} \hbar V \sum_n \frac{\mel{\psi_H^0}{\hat{\psi}_{\beta}^\dagger(0)}{N_g-1,n,-\vb{k}}^* \mel{N_g-1,n,-\vb{k}}{\hat{\psi_{\alpha}}(0)}{\psi_H^0}^*}{\hbar\omega - \mu + \epsilon_{n,-\vb{k}}(N_g-1)-i\eta}\\[.2cm] &= \hbar V \sum_{n} \frac{\mel{N_g+1,n,\vb{k}}{\hat{\psi}_{\alpha}^\dagger(0)}{\psi_H^0} \mel{\psi_H^0}{\hat{\psi}_{\beta}(0)}{N_g+1,n,\vb{k}}}{\hbar\omega-\mu - \epsilon_{n,\vb{k}}(N_g+1)-i\eta}\\[.2cm] &\quad {}+\hbar V \sum_n \frac{\mel{N_g-1,n,-\vb{k}}{\hat{\psi}_{\beta}(0)}{\psi_H^0}\mel{\psi_H^0}{\hat{\psi}_{\alpha}^\dagger(0)}{N_g-1,n,-\vb{k}}}{\hbar\omega - \mu + \epsilon_{n,-\vb{k}}(N_g-1)-i\eta}\\[.2cm] &= G_{\beta\alpha}^A (\vb{k},\omega). \end{align*}\]∎
The retarded and advanced Green’s functions differ from each other and from the time-ordered Green’s function only in the convergence factors $\pm i\eta$, which are important near the singularities. If $\omega$ is real and greater than $\hbar^{-1}\mu$, then the infinitesimal imaginary parts $\pm i\eta$ in the second term of $\eqref{lehmann representation for G}$ and $\eqref{lehmann representation for G R}$, $\eqref{lehmann representation for G A}$ play no role. And $\omega < \hbar^{-1}\mu$ is similar.
If we already know $G^{R}$ and want to get $G$, then
\[\begin{equation} \begin{cases} G_{\alpha\beta}(\vb{k},\omega) = G_{\alpha\beta}^{R}(\vb{k},\omega) , \quad &\omega> \mu,\\[.2cm] G_{\alpha\beta}(\vb{k},\omega) = [G^{R}_{\beta\alpha}(\vb{k},\omega)]^*, & \omega <\mu. \end{cases} \end{equation}\]$G^{A}\longrightarrow G$,
\[\begin{equation} \begin{cases} G_{\alpha\beta}(\vb{k},\omega) = [G_{\beta\alpha}^{A}(\vb{k},\omega)]^* , \quad &\omega> \mu,\\[.2cm] G_{\alpha\beta}(\vb{k},\omega) = G^{A}_{\alpha\beta}(\vb{k},\omega), & \omega <\mu. \end{cases} \end{equation}\]$G\longrightarrow G^R$,
\[\begin{equation} \begin{cases} G^R_{\alpha\beta}(\vb{k},\omega) = G_{\alpha\beta}(\vb{k},\omega) , \quad &\omega> \mu,\\[.2cm] G^R_{\alpha\beta}(\vb{k},\omega) = G^*_{\beta\alpha}(\vb{k},\omega), & \omega <\mu. \end{cases} \end{equation}\]$G\longrightarrow G^{A}$,
\[\begin{equation} \begin{cases} G^A_{\alpha\beta}(\vb{k},\omega) = G_{\beta\alpha}^*(\vb{k},\omega) , \quad &\omega> \mu,\\[.2cm] G^A_{\alpha\beta}(\vb{k},\omega) = G_{\alpha\beta}(\vb{k},\omega), & \omega <\mu. \end{cases} \end{equation}\]
3. Interaction independent of spin
3.1. Spectral functions
If the interaction is independent of particle’s spin, then
\[\begin{gather} G_{\alpha\beta} = G \delta_{\alpha\beta},\quad G = \frac{1}{2s+1} \sum_{\alpha}G_{\alpha\alpha},\\[.2cm] G_{\alpha\beta}^{R,A} = G^{R,A} \delta_{\alpha\beta},\quad G^{R,A} = \frac{1}{2s+1} \sum_{\alpha}G^{R,A}_{\alpha\alpha} , \end{gather}\]which have been shown in previous post. So the Lehmann representation of the single-particle Green’s function $\eqref{lehmann representation for G}$ becomes
\[\begin{equation} \begin{split} G(\vb{k},\omega) = \frac{\hbar V}{2s+1}\sum_{\alpha}\sum_{n} \Bigg[ &\frac{\abs{\mel{N_g+1,E_n(N_g+1),\vb{k}}{\hat{\psi}_{\alpha}^\dagger(0)}{\psi_H^0}}^2}{\hbar \omega - \mu - \epsilon_{n,\vb{k}}(N_g+1)+i\eta} \\[.2cm] &\quad {}+ \frac{\abs{\mel{N_g-1,E_n(N_g-1),\vb{k}}{\hat{\psi}_{\alpha}(0)}{\psi_H^0}}^2}{\hbar \omega - \mu + \epsilon_{n,-\vb{k}}(N_g-1)-i\eta} \Bigg] \end{split} \end{equation}\]And we introduce two positive-definite weight functions $A(\vb{k},\omega)$ and $B(\vb{k},\omega)$ called the spectral functions:
So $G(\vb{k},\omega)$ becomes
\[\begin{equation} G(\vb{k},\omega) = \int_0^{\infty} \dd{\omega'} \qty[\frac{A(\vb{k},\omega')}{\omega - \hbar^{-1}\mu - \omega ' +i\eta} + \frac{B(\vb{k},\omega')}{\omega -\mu +\omega' -i\eta} ]. \end{equation}\]A similar analysis for the retarded and advanced Green’s functions yields
\[\begin{equation} G^{R,A}(\vb{k},\omega) = \int_0^{\infty}\dd{\omega'} \qty[\frac{A(\vb{k},\omega')}{\omega - \hbar^{-1}\mu - \omega' \pm i\eta} + \frac{B(\vb{k},\omega')}{\omega - \hbar^{-1}\mu +\omega' \pm i\eta}]. \end{equation}\]So all three Green’s functions can be constructed if $A$ and $B$ are known.
Exercise
Prove the following equation:
\[\begin{equation} \int_0^{\infty} \dd{\omega} [A(\vb{k},\omega) + B(\vb{k},\omega)]=1. \end{equation}\]For $\abs{\omega}\to\infty$, we find
\[\begin{equation} \lim_{\abs{\omega}\to\infty} G(\vb{k},\omega) = \lim_{\abs{\omega}\to\infty}G^{R,A}(\vb{k},\omega) =\frac{1}{\omega} \int_0^{\infty} \dd{\omega'} \qty[A(\vb{k},\omega') + B(\vb{k},\omega')] = \frac{1}{\omega}. \label{green function for large omega} \end{equation}\]In addition, the symbolic identity (Sokhotski-Plemelj theorem) valid for real $\omega$
\[\begin{equation} \frac{1}{\omega \pm i\eta} = \mathcal{P}\frac{1}{\omega} \mp i\pi \delta(\omega), \label{Sokhotski-Plemelj theorem} \end{equation}\]where $\mathcal{P}$ denotes the Cauchy principle value. Then
\[\begin{align} & \mathrm{Re}\ G(\vb{k},\omega) = \mathrm{Re} \ G^{R}(\vb{k},\omega) = \mathrm{Re}\ G^{A}(\vb{k},\omega),\\[.2cm] & \mathrm{Im}\ G^R(\vb{k},\omega) = \mathrm{sign}(\omega -\mu) \mathrm{Im}\ G(\vb{k},\omega),\\[.2cm] &\mathrm{Im}\ G^A(\vb{k},\omega) = -\mathrm{sign}(\omega-\mu) \mathrm{Im}\ G(\vb{k},\omega). \end{align}\]Through it we can also get the relations $\eqref{relation 1}$, $\eqref{relation 2}$ and $\eqref{relation 3}$.
3.2. Dispersion relations
This can be proved with $\eqref{Sokhotski-Plemelj theorem}$ directly. However, we will use another method, namely the contour integration to prove it.
Proof of $G^{R,A}$
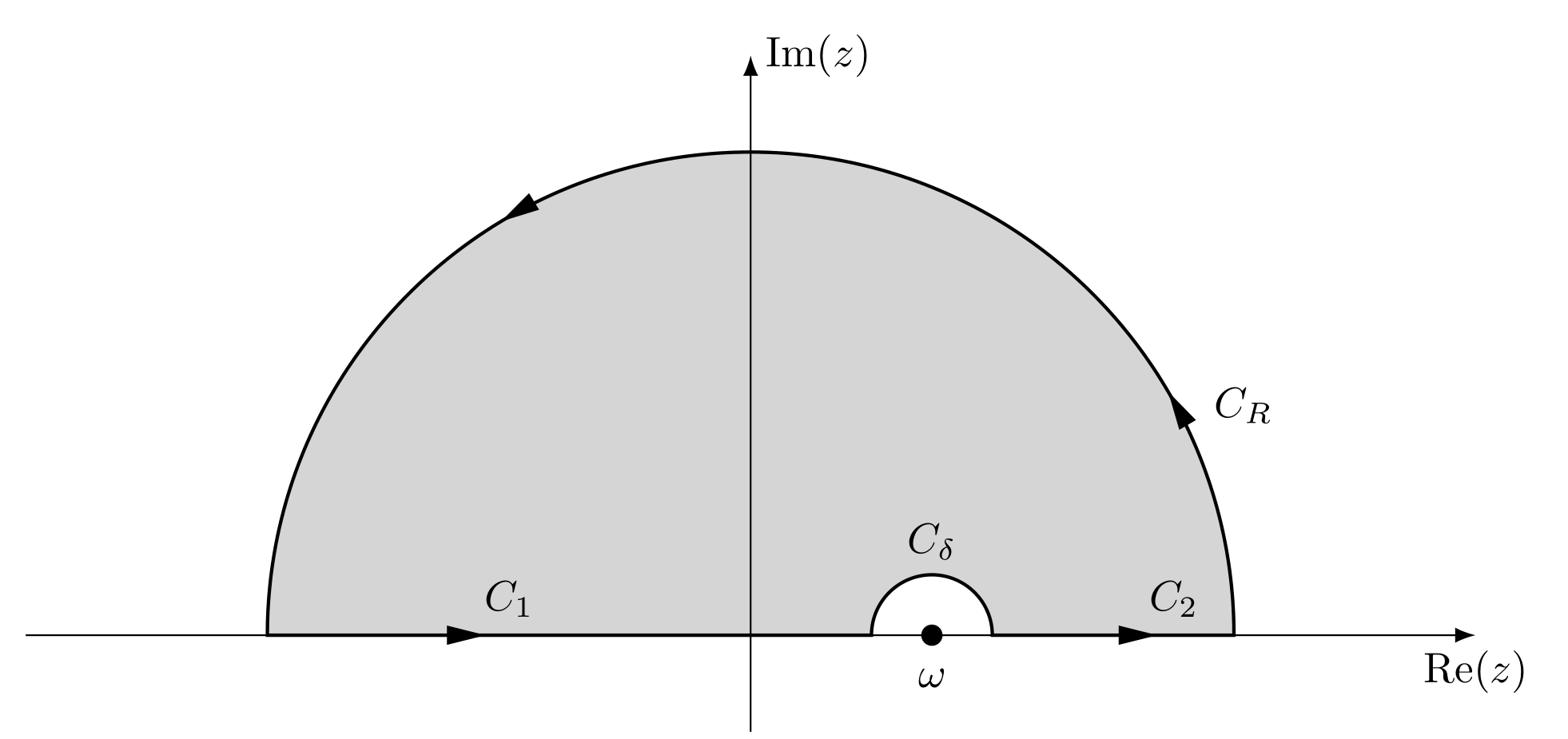
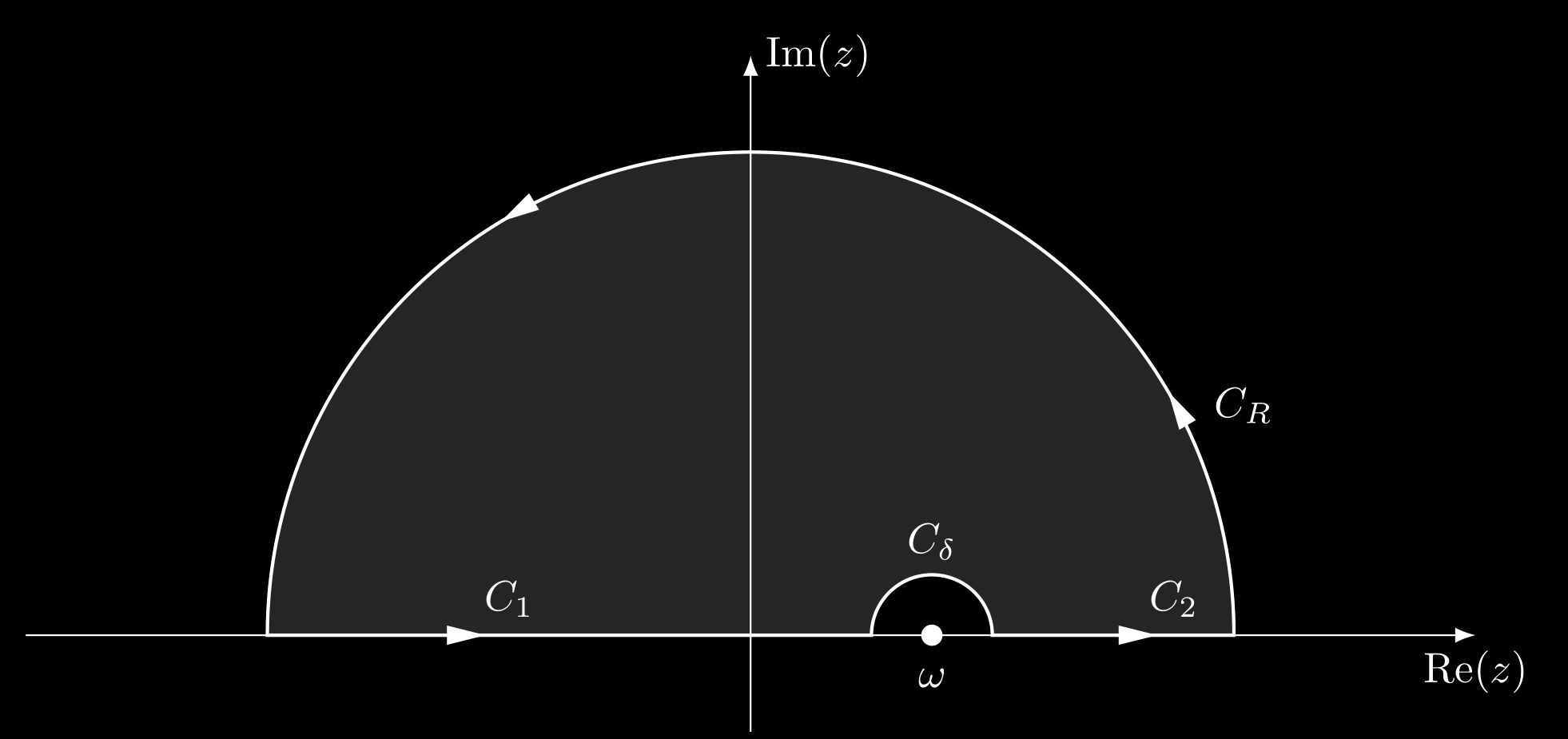
Consider the following contour integration
\[I_C = \oint_{C} \frac{G^{R}(\vb{k},z)}{z-\omega} \dd{z} = \left(\int_{C_R} + \int_{C_{\delta}} + \int_{C_1}+\int_{C_2}\right)\frac{G^{R}(\mathbf{k},z)}{z-\omega}\dd{z},\]where the contour $C$ is the upper half circle in $z$ plane.
Tikz code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
\documentclass[border=10pt]{standalone}
\usepackage{tikz}
\usetikzlibrary{arrows.meta,decorations.markings,calc,bending,shadows}
\begin{document}
\begin{tikzpicture}[>={Kite[inset=0pt,length=0.32cm,bend]},
decoration={markings,
mark= at position .1 with {\arrow{>}},
mark= at position .4 with {\arrow{>}},
mark= at position 0.68 with {\arrow{>}},
mark= at position 0.97 with {\arrow{>}},
}]
\def\radius{4}
\def\littleradius{0.5}
% contour
\filldraw[postaction = {decorate}, thick ,fill=gray!40]
(0:\radius) arc (0:180:\radius) --
(1,0) arc (180:0:\littleradius) -- cycle;
% pole
\fill (1.5,0)node[yshift=22pt]{$C_{\delta}$} node[yshift=-10pt]{$\omega$} circle(2.5pt);
\node at (25:\radius+0.5){$C_R$};
\node at (-2,0.3){$C_1$};
\node at (3.5,0.3){$C_2$};
% axes
\draw[-Latex] (-1.5*\radius,0) -- (1.5*\radius,0) node[below]{$\mathrm{Re}(z)$} ;
\draw[-Latex] (0,-0.2*\radius) -- (0,1.2*\radius) node[right]{$\mathrm{Im}(z)$};
\end{tikzpicture}
\end{document}
Because we know $\eqref{green function for large omega}$, so the integral over $C_{R}$ is zero. And the retarded Green’s function is analytic on the upper half $z$ plane, the whole contour integral is equal to zero too. For integral over $C_{\delta}$, we can use the estimation lemma to get
\[\int_{C_\delta} \frac{G^{R}(\vb{k},z)}{z-\omega}\dd{z} = -i\pi G^{R}(\vb{k},\omega).\]Thus,
\[\begin{gather*} I_{C_1} + I_{C_2} = \mathcal{P} \int_{-\infty}^{\infty}\frac{G^{R}(\vb{k},\omega')}{\omega'-\omega} \dd{\omega'} = -I_{C_\delta} = i\pi G^{R}(\vb{k},\omega), \\[.2cm] \Rightarrow \quad \mathcal{P}\int_{-\infty}^{\infty}\frac{\mathrm{Re}\ G^{R}(\vb{k},\omega') + i\ \mathrm{Im}\ G^{R}(\vb{k},\omega')}{\omega'-\omega}\dd{\omega'} = i \pi \qty[\mathrm{Re}\ G^{R}(\vb{k},\omega') + i\ \mathrm{Im}\ G^{R}(\vb{k},\omega') ]. \end{gather*}\]Comparing the real part and image part respectively, we can get desired results:
\[\begin{align*} &\mathrm{Re}\ G^{R}(\vb{k},\omega) = \mathcal{P}\frac{1}{\pi} \int_{-\infty}^{\infty}\dd{\omega'} \frac{\mathrm{Im}\ G^{R}(\vb{k},\omega')}{\omega'-\omega},\\[.2cm] &\mathrm{Im}\ G^{R}(\vb{k},\omega) =-\mathcal{P}\frac{1}{\pi} \int_{-\infty}^{\infty}\dd{\omega'} \frac{\mathrm{Im}\ G^{R}(\vb{k},\omega')}{\omega'-\omega}. \end{align*}\]The same method can be used to prove dispersion relations of $G^{A}$, but we need to choose the lower half $z$ plane since $G^A$ is analytic on the lower half $z$ plane. So
\[\begin{align*} &\mathrm{Re}\ G^{A}(\vb{k},\omega) = - \mathcal{P}\frac{1}{\pi} \int_{-\infty}^{\infty}\dd{\omega'} \frac{\mathrm{Im}\ G^{A}(\vb{k},\omega')}{\omega'-\omega},\\[.2cm] &\mathrm{Im}\ G^{A}(\vb{k},\omega) = \mathcal{P}\frac{1}{\pi} \int_{-\infty}^{\infty}\dd{\omega'} \frac{\mathrm{Im}\ G^{A}(\vb{k},\omega')}{\omega'-\omega}. \end{align*}\]∎
Proof of $G$
For single-particle Green’s function, we have
\[\begin{align*} \mathrm{Re}\ G(\vb{k},\omega)& = \mathrm{Re}\ G^{R}(\vb{k},\omega) = \mathcal{P}\frac{1}{\pi} \int_{-\infty}^{\infty}\dd{\omega'} \frac{\mathrm{Im}\ G^{R}(\vb{k},\omega')}{\omega'-\omega}\\[.2cm] &= \mathcal{P}\frac{1}{\pi} \int_{-\infty}^{\hbar^{-1}\mu}\dd{\omega'} \frac{\mathrm{Im}\ G^{R}(\vb{k},\omega')}{\omega'-\omega} + \mathcal{P}\frac{1}{\pi} \int_{\hbar^{-1}\mu}^{\infty}\dd{\omega'} \frac{\mathrm{Im}\ G^{R}(\vb{k},\omega')}{\omega'-\omega}\\[.2cm] &=-\mathcal{P}\frac{1}{\pi} \int_{-\infty}^{\hbar^{-1}\mu}\dd{\omega'} \frac{\mathrm{Im}\ G^{A}(\vb{k},\omega')}{\omega'-\omega} + \mathcal{P}\frac{1}{\pi} \int_{\hbar^{-1}\mu}^{\infty}\dd{\omega'} \frac{\mathrm{Im}\ G^{R}(\vb{k},\omega')}{\omega'-\omega}\\[.2cm] &=\mathcal{P}\frac{1}{\pi} \int_{-\infty}^{\hbar^{-1}\mu}\dd{\omega'} \frac{\mathrm{sign}(\omega'-\hbar^{-1}\mu)\mathrm{Im}\ G(\vb{k},\omega')}{\omega'-\omega} + \mathcal{P}\frac{1}{\pi} \int_{\hbar^{-1}\mu}^{\infty}\dd{\omega'} \frac{\mathrm{sign}(\omega'-\hbar^{-1}\mu)\mathrm{Im}\ G^{R}(\vb{k},\omega')}{\omega'-\omega}\\[.2cm] &=\mathcal{P}\frac{1}{\pi}\int_{-\infty}^{\infty}\dd{\omega'} \frac{\mathrm{Im}\ G(\vb{k},\omega')}{\omega'-\omega}\mathrm{sign}(\omega'-\hbar^{-1}\mu). \end{align*}\]A similar analysis for $\mathrm{Im}\ G(\vb{k},\omega)$ yields
\[\begin{align*} \mathrm{Im}\ G(\vb{k},\omega) &=\theta(\omega - \hbar^{-1}\mu) \mathrm{Im}\ G^{R}(\vb{k},\omega) + \theta(\mu - \hbar^{-1}\omega) \mathrm{Im}\ G^{A}(\vb{k},\omega)\\[.2cm] &=\theta(\omega-\hbar^{-1}\mu)\qty(-\mathcal{P}\frac{1}{\pi} \int_{-\infty}^{\infty}\frac{\mathrm{Re}\ G(\vb{k},\omega')}{\omega'-\omega}\dd{\omega'}) + \theta(\hbar^{-1}\mu-\omega) \qty(\mathcal{P}\frac{1}{\pi}\int_{-\infty}^{\infty}\frac{\mathrm{Re}\ G(\vb{k},\omega')}{\omega'-\omega}\dd{\omega'})\\[.2cm] &= - \mathcal{P} \frac{1}{\pi}\mathrm{sign} (\omega-\hbar^{-1}\mu) \int_{-\infty}^{\infty}\dd{\omega'} \frac{\mathrm{Re}\ G(\vb{k},\omega')}{\omega'-\omega}. \end{align*}\]∎
4. References
- Fetter, A. L., Walecka, J. D., Quantum Theory of Many-Particle Systems. Courier Corporation. (2002)
- Mahan, G. D., Many-Particle Physics. Springer Science+Business Media, LLC. (2000).
- Altland, A., Simons, B. D., Condensed Matter Field Theory. Cambridge University Press. (2010)
- 金彪. 量子多体理论. 2024年春