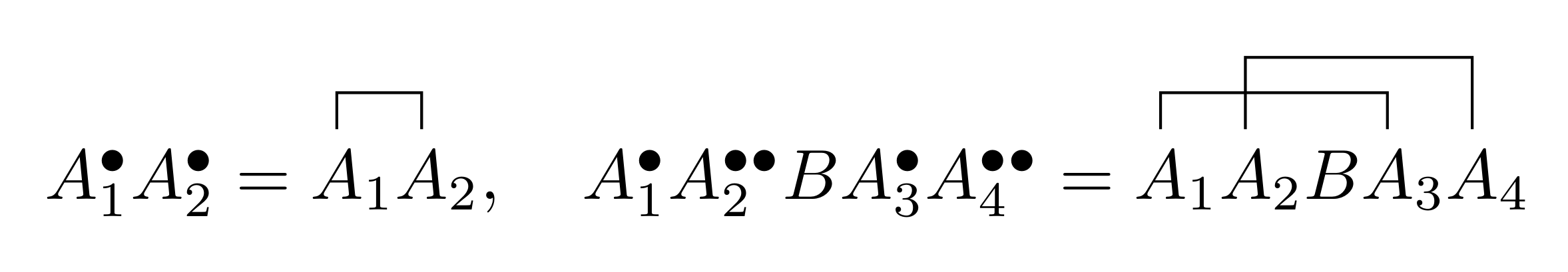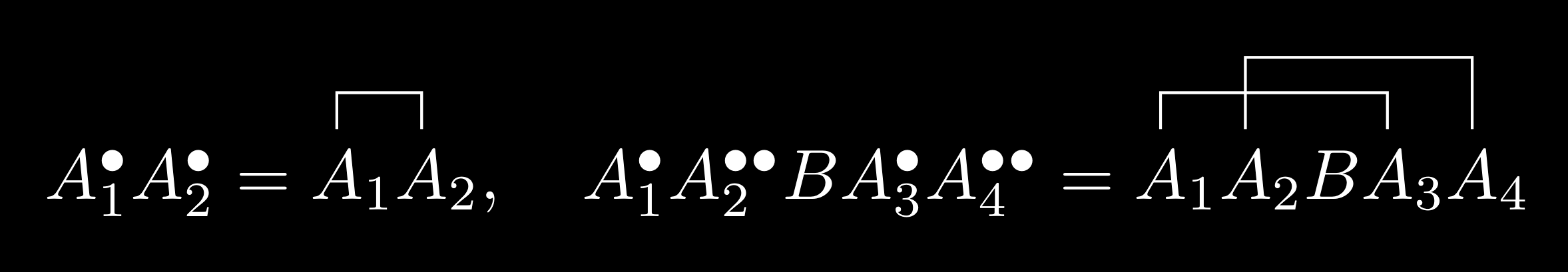§2.3 Wick's Theorem (Fermions)
Preceding posts defined the single-particle Green’s function and exhibited its relation to observable properties. However, we still do not know how to calculate $G$ for nontrivial physical system. As our general method of attack, we shall evaluate the Green’s function with perturbation theory. This procedure is most easily carried out in the interaction picture, where the various terms can be enumerated with a theorem of Wick. We will derive Wick’s theorem in this post which is very useful with Feynman diagram in perturbation theory.
1. Green’s function in the interaction picture
In previous post, we defined the single-particle Green’s function in Heisenberg picture,
\[i G_{\alpha\beta}(\vb{x},t;\vb{x}',t') := \bra{\psi_{H}^{0}} \hat{\mathsf{T}}\qty[\hat{\psi}_{H\alpha}(\vb{x},t)\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')]\ket{\psi_H^{0}},\]but it is not convenient for perturbation theory with Hamiltonian $\hat{H} = \hat{H}_0 + \hat{V}$. We must switch it to the interaction picture.
where $\hat{S}(t,t_0)$ is the time evolution operator in the interaction picture and $\ket{\psi_H^0} = \ket{\psi_I(t_0)} = \ket{\psi_S(t_0)}$.
Proof
Switch $\hat{\mathsf{T}}\qty[\hat{\psi}_{H\alpha}(\vb{x},t)\hat{\psi}_{H\beta}^\dagger(\vb{x}’,t’)]$ to the interaction picture:
\[\begin{align*} \hat{\mathsf{T}}\qty[\hat{\psi}_{H\alpha}(\vb{x},t)\hat{\psi}_{H\beta}^\dagger(\vb{x}',t')] & = \theta(t-t')\hat{\psi}_{H\alpha}(\vb{x},t) \hat{\psi}_{H\beta}^\dagger(\vb{x}',t') - \theta(t'-t) \hat{\psi}_{H\beta}^\dagger(\vb{x}',t')\hat{\psi}_{H\alpha}(\vb{x},t)\\[.2cm] &= \theta(t-t')\hat{S}^\dagger(t,t_0)\hat{\psi}_{I\alpha}(\vb{x},t)\hat{S}(t,t_0)\hat{S}^\dagger(t',t_0)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(t',t_0)\\[.2cm] &\quad {}-\theta(t'-t)\hat{S}^\dagger(t',t_0)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(t',t_0)\hat{S}^\dagger(t,t_0)\hat{\psi}_{I\alpha}(\vb{x},t)\hat{S}(t,t_0)\\[.2cm] &= \theta(t-t')\hat{S}(t_0,t)\textcolor{crimson}{\mathbb{1}}\hat{\psi}_{I\alpha}(\vb{x},t)\hat{S}(t,t')\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(t',t_0)\\[.2cm] &\quad {} -\theta(t'-t)\hat{S}(t_0,t')\textcolor{crimson}{\mathbb{1}}\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(t',t)\hat{\psi}_{I\alpha}(\vb{x},t)\hat{S}(t,t_0)\\[.2cm] &= \theta(t-t')\hat{S}(t_0,t)\textcolor{crimson}{\hat{S}(t,\infty)\hat{S}(\infty,t)}\hat{\psi}_{I\alpha}(\vb{x},t)\hat{S}(t,t')\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(t',t_0)\\[.2cm] &\quad {} -\theta(t'-t)\hat{S}(t_0,t')\textcolor{crimson}{\hat{S}(t',\infty)\hat{S}(\infty,t')}\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(t',t)\hat{\psi}_{I\alpha}(\vb{x},t)\hat{S}(t,t_0)\\[.2cm] &=\theta(t-t')\hat{S}(t_0,\infty)\hat{\mathsf{T}}\qty[\hat{S}(\infty,t)\hat{\psi}_{I\alpha}(\vb{x},t)\hat{S}(t,t')\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(t',t_0)]\\[.2cm] &\quad {} -\theta(t'-t)\hat{S}(t_0,\infty)\hat{\mathsf{T}}\qty[\hat{S}(\infty,t')\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(t',t)\hat{\psi}_{I\alpha}(\vb{x},t)\hat{S}(t,t_0)]\\[.2cm] &= \theta(t-t')\hat{S}(t_0,\infty)\hat{\mathsf{T}}\qty[\hat{\psi}_{I\alpha}(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(\infty,t_0)]\\[.2cm] &\quad {} - \theta(t'-t) \hat{S}(t_0,\infty) \hat{\mathsf{T}}\qty[\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{\psi}_{I\alpha}(\vb{x},t)\hat{S}(\infty,t_0)]\\[.2cm] &=\qty[\theta(t-t') + \theta(t'-t)]\hat{S}(t_0,\infty) \hat{\mathsf{T}} \qty[\hat{\psi}_{I\alpha}(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(\infty,t_0)]\\[.2cm] &=\hat{S}(t_0,\infty) \hat{\mathsf{T}} \qty[\hat{\psi}_{I\alpha}(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(\infty,t_0)]. \end{align*}\]Note that we only discuss the case of fermions. Substituting the above results into the definition of $G$, we reach the desire result:
\[iG_{\alpha\beta}(\vb{x},t;\vb{x}',t')=\ev{\hat{S}(t_0,\infty)\hat{\mathsf{T}}\qty[\hat{\psi}_{I\alpha}(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x',t'})\hat{S}(\infty,t_0)]}{\psi_H^0},\]∎
One more thing to note, $\ket{\psi_H^0}$ is the exact ground state which satisfies $\hat{H}\ket{\psi_H^0} = E_g \ket{\psi_H^0}$. We can not solve $\ket{\psi_H^0}$ exactly because of $\hat{V}$, however, we can solve the ground state $\ket{\Phi_H^0}$ exactly without interaction $\hat{V}$. Namely, we have $\hat{H}_0 \ket{\Phi_H^0} = E_g^0 \ket{\Phi_H^0}$. So to take this one step further, we need to switch $\ket{\psi_H^0}$ to $\ket{\Phi_H^0}$.
where $\hat{S}(\infty,-\infty) = \hat{S}$ is the $S$-matrix and
\[\begin{equation} \hat{S}(-\infty,\infty) = \hat{\mathsf{T}} \exp\qty[-\frac{i}{\hbar} \int_{-\infty}^{\infty}\dd{t}'\hat{V}_I(t')],\quad \hat{V}_I(t) = \e^{i\hat{H}_0(t-t_0)/\hbar}\hat{V}\e^{-i\hat{H}_0(t-t_0)}. \end{equation}\]Proof
The original Hamiltonian is $\hat{H} = \hat{H}_0 + \hat{V}$. We define a new Hamiltonian $\hat{H}_{\epsilon}(t) = \hat{H}_0 + \hat{V}\e^{-\epsilon\abs{t-t_0}}$ and
\[\begin{gather*} \lim_{\epsilon\to 0^+}\hat{H}_{\epsilon} (t) = \lim_{\epsilon\to 0^+}\qty( \hat{H}_0 + \hat{V}\e^{-\epsilon\abs{t-t_0}}) = \hat{H}_0 + \hat{V} = \hat{H},\\[.2cm] \hat{H}_{\epsilon}(\pm \infty) = \hat{H}_{\epsilon}(t_0) = \hat{H}_0. \end{gather*}\]If $\epsilon$ is small enough, $\hat{H}_{\epsilon}(t)$ evolves very slowly with time, equivalent to an adiabatic process.
According to the adiabatic theorem in quantum mechanics, a quantum system that begins in the nondegenerate ground state of a time-dependent Hamiltonian will remain in the instantaneous ground state provided the Hamiltonian changes sufficiently slowly.
For the eigenstate $\ket{\psi_I(t)}$ of $\hat{H}_{\epsilon I}(t)$, we have $\ket{\psi_I(t_0)} = \hat{S}_{\epsilon}(t_0,-\infty)\ket{\psi_I(-\infty)}$ and
\[\begin{gather*} \hat{H}_{\epsilon I}(-\infty)\ket{\psi_I(-\infty)} = E_g^0\ket{\psi_I(-\infty)}, \quad \hat{H}_{\epsilon I}(-\infty) = \e^{i\hat{H_0}(t-t_0)/\hbar} \hat{H}_{\epsilon}(-\infty)\e^{-i\hat{H}_0(t-t_0)/\hbar} = \hat{H}_0,\\[.2cm] \Rightarrow\quad \hat{H}_0 \ket{\psi_I(-\infty)} = E_g^0\ket{\psi_I(-\infty)}. \end{gather*}\]We can choose $\ket{\psi_I(-\infty)} = \ket{\Phi_0}$, then $\ket{\psi_H^0}$ can be expressed via $\ket{\Phi^0}$:
\[\begin{equation*} \ket{\psi_H^0} = \ket{\psi_I(t_0)} = \hat{S}_{\epsilon}(t_0,-\infty)\ket{\psi_I(-\infty)} = \hat{S}_{\epsilon}(t_0,-\infty) \ket{\Phi^0}. \end{equation*}\]On the other hand,
\[\begin{gather*} \hat{H}_{\epsilon I}(\infty)\ket{\psi_I(\infty)} = E_g^0 \ket{\psi_I(\infty)}, \quad \hat{H}_{\epsilon I} = \hat{H}_0\\[.2cm] \Rightarrow \quad \hat{H}_0 \ket{\psi _I(\infty)} = E_g^0 \ket{\psi_I(\infty)}. \end{gather*}\]Because we let $\ket{\psi_I(-\infty)} = \ket{\Phi^0}$, $\ket{\psi_I(\infty)}$ is not always equal to $\ket{\Phi^0}$, they differ by at most a phase,
\[\begin{equation*} \ket{\psi_I(\infty)}= \hat{S}_{\epsilon}(\infty,t_0) \ket{\psi_I(t_0)} = \hat{S}_{\epsilon}(\infty,t_0)\ket{\psi_H^0} =\mathrm{e}^{iL}\ket{\Phi^0}. \end{equation*}\]The Green’s function therefore becomes
\[\begin{align*} i G_{\alpha\beta}(\vb{x},t;\vb{x}',t') &= \ev{\hat{S}_{\epsilon}(t_0,\infty)\hat{\mathsf{T}}\qty[\hat{\psi}_{I\alpha}(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(\infty,t_0)]}{\psi_H^0}\\[.2cm] &=\mel{\psi_H^0}{\hat{S}_{\epsilon}(t_0,\infty)\hat{\mathsf{T}}\qty[\hat{\psi}_{I\alpha}(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}(\infty,t_0)]\hat{S}_{\epsilon}(t_0,-\infty)}{\Phi^0}\\[.2cm] &=\mel{\psi_H^0}{\hat{S}_{\epsilon}(t_0,\infty)\hat{\mathsf{T}}\qty[\hat{\psi}_{I\alpha}(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}_{\epsilon}(\infty,-\infty)]}{\Phi^0}\\[.2cm] &=\e^{-iL}\ev{\hat{\mathsf{T}}\qty[\hat{\psi}_{I\alpha}(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}_{\epsilon}(\infty,-\infty)]}{\Phi^0}. \end{align*}\]We still do not know what is $L$. Considering the normalization of $\ket{\psi_H^0}$, we have
\[\begin{align*} &\ket{\psi_H^0} = \e^{iL}\hat{S}_{\epsilon}(t_0,\infty)\ket{\Phi^0},\quad \ket{\psi_H^0} = \hat{S}_{\epsilon}(t_0,-\infty)\ket{\Phi^0},\\[.2cm] \Rightarrow \quad& 1 = \braket{\psi_H^0} = \e^{-iL}\bra{\Phi^0}\hat{S}_{\epsilon}(\infty,t_0)\hat{S}_{\epsilon}(t_0,-\infty)\ket{\Phi^0} = \e^{-iL}\ev{\hat{S}_{\epsilon}(\infty,-\infty)}{\Phi^0}\\[.2cm] \Rightarrow \quad& \e^{-iL} = \frac{1}{\ev{\hat{S}_\epsilon(\infty,-\infty)}{\Phi^0}}. \end{align*}\]Finally, let $\epsilon\to 0^+$, the exact Green’s function may be written as
\[iG_{\alpha\beta}(\vb{x},t;\vb{x}',t') = \frac{\ev{\hat{\mathsf{T}}\qty[\hat{\psi}_{I\alpha}(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{S}_{\epsilon}(\infty,-\infty)]}{\Phi^0}}{\ev{\hat{S}(\infty,-\infty)}{\Phi^0}}.\]∎
In perturbation theory, it is very useful to expand the $S$-matrix into a series:
\[\begin{equation} \hat{S}(\infty,-\infty) = \sum_{n=0}^{\infty}\frac{1}{n!} \qty(\frac{-i}{\hbar})^n \int_{-\infty}^{\infty}\dd{t_1}\int_{-\infty}^{\infty}\dd{t_2} \cdots \int_{-\infty}^{\infty}\dd{t_n} \hat{\mathsf{T}}\qty[\hat{V}_I(t_1)\hat{V}_I(t_2)\cdots\hat{V}_I(t_n)]. \end{equation}\]And the Green’s function becomes
\[\begin{equation} \begin{split} iG_{\alpha\beta}(\vb{x},t;\vb{x}',t') = \sum_{n=0}^{\infty}\frac{1}{n!}&\qty(\frac{-i}{\hbar})^n \int_{-\infty}^{\infty}\dd{t_1} \cdots \int_{-\infty}^{\infty}\dd{t_n}\\[.2cm] &{}\times \frac{\ev{\hat{\mathsf{T}}\qty[\hat{\psi}_{I\alpha}(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')V_I(t_1)\cdots V_I(t_n)]}{\Phi^0}}{\ev{\hat{S}(\infty,-\infty)}{\Phi^0}}. \end{split} \label{green-function} \end{equation}\]If the interaction is independent of particle’s spin which means
\[\begin{equation} \begin{split} \hat{V}_I(t) &= \e^{i\hat{H}_0(t-t_0)/\hbar}\hat{V}\e^{-i\hat{H}_0(t-t_0)/\hbar}\\[.2cm] &=\frac{1}{2}\sum_{\alpha}\sum_{\beta} \int\dd[3]{x}\int\dd[3]{x'} \hat{\psi}_{I\alpha}^\dagger(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t)\hat{V}(\vb{x},\vb{x}')\hat{\psi}_{I\beta}(\vb{x}',t)\hat{\psi}_{I\alpha}(\vb{x},t). \end{split} \label{interaction} \end{equation}\]It is convenient to rewrite the interparticle potential $\hat{V}$ as
\[\begin{equation} \hat{U}(\vb{x},t;\vb{x}',t') = \hat{V}(\vb{x},\vb{x}')\delta(t-t'). \end{equation}\]And
\[\begin{equation} \int_{-\infty}^{\infty}\hat{U}(\vb{x},t;\vb{x}',t')\dd{t'} = \int_{-\infty}^{\infty}\dd{t'}\hat{V}(\vb{x},\vb{x}')\delta(t-t') = \hat{V}(\vb{x},\vb{x}'). \end{equation}\]So $\eqref{interaction}$ can be rewritten as
\[\begin{equation} \hat{V}_I(t) = \frac{1}{2}\sum_{\alpha\beta}\int_{-\infty}^{\infty}\dd{t}' \iint \dd[3]{x}\dd[3]{x'} \hat{\psi}_{I\alpha}^\dagger(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{U}(\vb{x},t;\vb{x}',t') \hat{\psi}_{I\beta}(\vb{x}',t') \hat{\psi}_{I\alpha}(\vb{x},t). \end{equation}\]Integrate both sides over time $t$,
\[\begin{equation} \int_{-\infty}^{\infty}\dd{t}\hat{V}_I(t) = \frac{1}{2} \sum_{\alpha\beta}\iint\dd[3]{x}\dd{t} \iint \dd[3]{x'}\dd{t'} \hat{\psi}_{I\alpha}^\dagger(\vb{x},t)\hat{\psi}_{I\beta}^\dagger(\vb{x}',t')\hat{U}(\vb{x},t;\vb{x}',t') \hat{\psi}_{I\beta}(\vb{x}',t') \hat{\psi}_{I\alpha}(\vb{x},t). \end{equation}\]It is also convenient to introduce the $4$-dimensional coordinates $x \to \qty{\vb{x},t}$, then
\[\begin{equation} \int_{-\infty}^{\infty} \hat{V}_I(t')\dd{t}' = \frac{1}{2}\sum_{\alpha\beta}\int\dd[4]{x}\int\dd[4]{x'} \hat{\psi}_{I\alpha}^\dagger(x)\hat{\psi}_{I\beta}^\dagger(x')\hat{U}(x,x') \hat{\psi}_{I\beta}(x') \hat{\psi}_{I\alpha}(x). \end{equation}\]Then the Green’s function in $\eqref{green-function}$ becomes (just show two leading terms):
\[\begin{equation} \begin{split} iG_{\alpha\beta}(x,x') =&\frac{1}{\ev{\hat{S}}{\Phi^0}}\Bigg[ i G_{\alpha\beta}^{0}(x,x') + \qty(\frac{-i}{\hbar}) \sum_{\lambda\lambda'\mu\mu'} \frac{1}{2} \iint\dd[4]{x_1}\dd[4]{x_1'} \hat{U}(x_1,x_1')\quad \\[.2cm] &{}\times \ev{\hat{\mathsf{T}}\qty[\psi_{I\alpha}(x)\hat{\psi}_{I\beta}(x')\hat{\psi}_{I\lambda}^\dagger(x_1)\hat{\psi}^\dagger_{I\lambda'}(x_1')\hat{\psi}_{I\lambda'}(x_1')\hat{\psi}_{I\lambda}(x_1)]}{\Psi^0} + \cdots \Bigg], \end{split} \label{green-function-expansion} \end{equation}\]where $iG_{\alpha\beta}^0(x,x’) = \ev{\hat{\mathsf{T}}\qty[\hat{\psi}_{I\alpha}(x)\hat{\psi}_{I\beta}(x’)]}{\Phi^0}$ refers to the noninteracting system. This expression shows that we must evaluate the expectation value in the nonintearcting ground state of $\hat{\mathsf{T}}$ products of creation and destruction operators of the form
\[\ev{\hat{\mathsf{T}}[\hat{\psi}_{I\alpha}(x)\hat{\psi}_{I\beta}^\dagger(y)\hat{\psi}^\dagger\cdots \hat{\psi}]}{\Phi^0}.\]This is quite complicate if we use commutation or anticommutation relations. However, we shall rely on Wick’s theorem, which provides a general procedure for evaluating such matrix elements.
2. Wick’s theorem
The essential idea is to move all destruction operators to the right, where they annihilate the noninteracting ground state. This lead to the concept of the normal ordering
2.1. Normal ordering
In quantum mechanics, if an operator $A$ acts on the vacuum state $\ket{0}$, the result is zero, i.e. $\hat{A}\ket{0} = 0$, we will call $\hat{A}$ an annihilation operator. Otherwise, $\hat{A}\ket{0} \neq 0$, we will call $\hat{A}$ a creation operator. But what we are dealing with here is not the vacuum state $\ket{0}$ but the noninteracting ground state $\ket{\Phi^0}$. For any operator $\hat{\psi}$,
\[\begin{align} & \hat{\psi}\ket{\Phi^0} = 0 \quad \Rightarrow \quad \text{$\hat{\psi}$ is an annihilation like operator}.\\[.2cm] & \hat{\psi}\ket{\Phi^0} \neq 0 \quad \Rightarrow \quad \text{$\hat{\psi}$ is a creation like operator}. \end{align}\]Consider the free fermion field where the Hamiltonian is $\displaystyle{\hat{H} = \hat{H}_0 = \sum_{\vb{k},\alpha}\epsilon_{\vb{k}}^0 \hat{C}_{\vb{k}\alpha}^\dagger \hat{C}_{\vb{k}\alpha}}$ and the ground state is $\displaystyle{\ket{\Phi_H^0} = \prod_{\vb{k}\leq k_F}\prod_{\alpha}\hat{C}_{\vb{k}\alpha}\ket{0}}$. For an operator $\hat{C}_{\vb{k}\alpha}$,
- In case of $\abs{\vb{k}}>k_F$, $\hat{C}_{\vb{k}\alpha}\ket{\Phi_H^0} = 0$, so $\hat{C}_{\vb{k}\alpha}$ is an annihilation like operator.
- In case of $\abs{\vb{k}}<k_F$, $\hat{C}_{\vb{k}\alpha}\ket{\Phi_H^0} \neq 0$, so $\hat{C}_{\vb{k}\alpha}$ is a creation like operator.
For an operator $\hat{C}_{\vb{k}\alpha}^\dagger$,
- In case of $\abs{\vb{k}}>k_F$, $\hat{C}_{\vb{k}\alpha}^\dagger\ket{\Phi_H^0} \neq 0$, so $\hat{C}_{\vb{k}\alpha}^\dagger$ is a creation like operator.
- In case of $\abs{\vb{k}}<k_F$, $\hat{C}_{\vb{k}\alpha}^\dagger\ket{\Phi_H^0} = 0$, so $\hat{C}_{\vb{k}\alpha}^\dagger$ is an annihilation like operator.
For most purposes, it is more convenient to use the field operators directly rather than the operators $\qty{\hat{C}_{\vb{k}\alpha}}$ referring to a single mode. In most systems of interest, field operators can be uniquely separated into a destruction part and a creation part. In plane wave representation, a field operator can be written as
\[\begin{align} \hat{\psi}_{I\alpha}(x) &= \e^{i\hat{H}_0(t-t_0)/\hbar} \hat{\psi}_{\alpha}(\vb{x})\e^{-i\hat{H}_0(t-t_0)/\hbar}\notag\\[.2cm] &= \frac{1}{\sqrt{V}} \sum_{\vb{k}} \e^{i\vb{k}\cdot\vb{x}} \e^{i\hat{H}_0(t-t_0)/\hbar} \hat{C}_{\vb{k}\alpha} \e^{-i\hat{H}_0(t-t_0)/\hbar}\notag \\[.2cm] &=\frac{1}{\sqrt{V}} \sum_{\vb{k}}\e^{i\vb{k}\cdot\vb{x}} \hat{C}_{\vb{k}\alpha}\e^{-i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}\notag\\[.2cm] &=\underbrace{\frac{1}{\sqrt{V}} \sum_{\abs{\vb{k}}>k_F} \hat{C}_{\vb{k}\alpha }\e^{i\vb{k}\cdot\vb{x} - i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}}_{\hat{\psi}^{(1)}_{I\alpha}(x)} + \underbrace{\frac{1}{\sqrt{V}} \sum_{\abs{\vb{k}}<k_F} \hat{C}_{\vb{k}\alpha }\e^{i\vb{k}\cdot\vb{x} - i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}}_{\hat{\psi}^{(2)}_{I\alpha}(x)}\notag \\[.2cm] &=\hat{\psi}^{(1)}_{I\alpha}(x) + \hat{\psi}^{(2)\dagger}_{I\alpha}(x). \end{align}\]So $\hat{\psi}^{(1)}_{I\alpha}(x)$ is a destruction part of $\hat{\psi}_{I\alpha}(x)$ (i.e. annihilation like operator) while $\hat{\psi}^{(2)\dagger}_{I\alpha}(x)$ is a creation parts of $\hat{\psi}_{I\alpha}(x)$ (i.e. creation like operator). Correspondingly, the adjoint operator becomes
\[\begin{equation} \hat{\psi}_{I\alpha}^\dagger(x) = \hat{\psi}^{(1)\dagger}_{I\alpha}(x) + \hat{\psi}^{(2)}_{I\alpha}(x). \end{equation}\]So $\hat{\psi}^{(1)\dagger}_{I\alpha}(x)$ is a creation part of $\hat{\psi}_{I\alpha}(x)$ while $\hat{\psi}^{(2)}_{I\alpha}(x)$ is a destruction parts of $\hat{\psi}_{I\alpha}(x)$ (i.e. creation like operator).
where
\[\begin{equation} \begin{cases} \displaystyle{\hat{\psi}^{(1)}_{I\alpha}(x) = \frac{1}{\sqrt{V}} \sum_{\abs{\vb{k}}>k_F} \hat{C}_{\vb{k}\alpha }\e^{i\vb{k}\cdot\vb{x} - i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}},\\[.2cm] \displaystyle{\hat{\psi}^{(2)}_{I\alpha}(x) = \frac{1}{\sqrt{V}} \sum_{\abs{\vb{k}}<k_F} \hat{C}_{\vb{k}\alpha}^\dagger\e^{-i\vb{k}\cdot\vb{x} + i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}}. \end{cases} \quad \begin{cases} \displaystyle{\hat{\psi}^{(1)\dagger}_{I\alpha}(x) = \frac{1}{\sqrt{V}} \sum_{\abs{\vb{k}}>k_F} \hat{C}_{\vb{k}\alpha }^\dagger\e^{-i\vb{k}\cdot\vb{x} + i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}},\\[.2cm] \displaystyle{\hat{\psi}^{(2)\dagger}_{I\alpha}(x) = \frac{1}{\sqrt{V}} \sum_{\abs{\vb{k}}<k_F} \hat{C}_{\vb{k}\alpha}\e^{i\vb{k}\cdot\vb{x} - i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}}. \end{cases} \end{equation}\]$\hat{\psi}_{I\alpha}^{(1)}$ and $\hat{\psi}_{I\alpha}^{(2)}$ are annihilation like operators, while $\hat{\psi}_{I\alpha}^{(1)\dagger}$ and $\hat{\psi}_{I\alpha}^{(2)\dagger}$ are creation like operators.
Normal ordering represents a different ordering of a product of field operators, in which all the annihilation like operators are placed to the right of all the creation like operators, again including a factor of $-1$ for every interchange of fermion operators.
By definition, we have following corollaries:
\[\begin{align} & \hat{\mathsf{N}}\qty[\hat{\psi}^{(1)\dagger}\hat{\psi}^{(2)\dagger}\hat{\psi}^{(1)}\hat{\psi}^{(2)}] = \hat{\psi}^{(1)\dagger}\hat{\psi}^{(2)\dagger}\hat{\psi}^{(1)}\hat{\psi}^{(2)},\\[.2cm] & \hat{\mathsf{N}}\qty[\hat{\psi}^{(1)}\hat{\psi}^{(2)}\hat{\psi}^{(1)\dagger}\hat{\psi}^{(2)\dagger}] = (-1)^4 \hat{\psi}^{(1)\dagger}\hat{\psi}^{(2)\dagger}\hat{\psi}^{(1)}\hat{\psi}^{(2)} = (-1)^{5}\hat{\psi}^{(1)\dagger}\hat{\psi}^{(2)\dagger}\hat{\psi}^{(2)}\hat{\psi}^{(1)},\\[.2cm] & \hat{\mathsf{N}}\qty[\hat{A}\hat{B}\hat{C}] = - \hat{\mathsf{N}}\qty[\hat{B}\hat{A}\hat{C}] = \hat{\mathsf{N}}[\hat{C}\hat{A}\hat{B}],\\[.2cm] & \hat{\mathsf{N}}\qty[\hat{A}\hat{B}\hat{C}] = \hat{A}\, \hat{\mathsf{N}}\qty[\hat{B}\hat{C}] \quad \text{if $\hat{A}$ is creation-like,}\\[.2cm] & \hat{\mathsf{N}}\qty[\hat{A}\hat{B}\hat{C}] = \hat{\mathsf{N}}\qty[\hat{A}\hat{B}]\hat{C}\quad \text{if $\hat{C}$ is annihilation-like,}\\[.2cm] & \hat{\mathsf{N}}\qty[\hat{A}\hat{B}\hat{C}] = - \hat{B}\, \hat{\mathsf{N}}\qty[\hat{A}\hat{C}] \quad \text{if $\hat{B}$ is creation-like,}\\[.2cm] & \hat{\mathsf{N}}\qty[\hat{A}\hat{B}\hat{C}] = - \hat{\mathsf{N}}\qty[\hat{A}\hat{C}]\hat{B}\quad \text{if $\hat{B}$ is annihilation-like,} \end{align}\]where $\hat{\mathsf{N}}$ is the normal-ordering operator.
A normal-ordered product of field operators is especially convenient because its expectation value in the unperturbed ground state $\ket{\Phi^0}$ vanishes identically.
Thus the ground state expectation value of a $\hat{\mathsf{T}}$ product of operators may be evaluated by reducing it to the corresponding $\hat{\mathsf{N}}$ product. NOte that both the $\hat{\mathsf{T}}$ product and the $\hat{\mathsf{N}}$ product are distributive. It is therefore sufficient to prove the theorem separately for creation or destruction parts.
2.2. Contractions
The contraction of two operators $\hat{A}$ and $\hat{B}$ is denoted $\hat{A}^{\bullet} \hat{B}^\bullet$ and is equal to the difference between the $\hat{\mathsf{T}}$ product and the $\hat{\mathsf{N}}$ product.
\[\begin{equation} \hat{A}^{\bullet} \hat{B}^\bullet : = \hat{\mathsf{T}}\qty[\hat{A}\hat{B}] - \hat{\mathsf{N}}\qty[\hat{A}\hat{B}]. \end{equation}\]Actually, this way of writing is just an alternative (just like Wick’s theorem in Wikipedia), I can’t draw a line joining $\hat{A}$ and $\hat{B}$ in MathJax. The reader should keep in mind that it can be converted to the traditional wick contraction notation.
The contraction represents the additional term introduced by rearranging a time-ordered product into a normal-ordered product and is therefore different for different time orderings of the operators. By definition, we have
$\displaystyle{\hat{A}^{\bullet}\hat{B}^{\bullet} = - \hat{B}^\bullet\hat{A}^\bullet.}$
Proof
\(\begin{align*} \hat{B}^\bullet(t_B)\hat{A}^\bullet(t_A) &= \hat{\mathsf{T}}\qty[\hat{B}(t_B)\hat{A}(t_A)] - \hat{\mathsf{N}}\qty[\hat{B}(t_B)\hat{A}(t_A)]\\[.2cm] &=-\hat{\mathsf{T}}\qty[\hat{A}(t_A)\hat{B}(t_B)] + \hat{\mathsf{N}}\qty[\hat{A}(t_A)\hat{B}(t_B)] = - \hat{B}^\bullet(t_B)\hat{A}(t_A). \end{align*}\)
∎
$\displaystyle{\hat{A}^{\bullet}\hat{B}^{\bullet} =0 }$, if $\displaystyle{\qty[\hat{A},\hat{B}]_+ = 0}$.
Proof
\[\begin{align*} \hat{A}^\bullet(t_A)\hat{B}^{\bullet}(t_B) &= \hat{\mathsf{T}} \qty[\hat{A}(t_A)\hat{B}(t_B)] - \hat{\mathsf{N}}\qty[\hat{A}(t_A)\hat{B}(t_B)]\\[.2cm] &=\theta(t_A-t_B)\hat{A}(t_A)\hat{B}(t_B) - \theta(t_B-t_A) \hat{B}(t_B)\hat{A}(t_A) - \hat{\mathsf{N}}\qty[\hat{A}(t_A)\hat{B}(t_B)]\\[.2cm] &=\theta(t_A-t_B)\hat{A}(t_A)\hat{B}(t_B) + \theta(t_B-t_A) \hat{A}(t_A)\hat{B}(t_B) - \hat{\mathsf{N}}\qty[\hat{A}(t_A)\hat{B}(t_B)]\\[.2cm] &=\hat{A}(t_A)\hat{B}(t_B) - \hat{\mathsf{N}}\qty[\hat{A}(t_A)\hat{B}(t_B)]\\[.2cm] \end{align*}\]Note that
\[\begin{equation*} \hat{\mathsf{N}}\qty[\hat{A}(t_A)\hat{B}(t_B)] = \begin{cases} \hat{A}(t_A)\hat{B}(t_B),\quad & \text{if $\hat{A}$ is creation-like,}\\[.2cm] -\hat{B}(t_B)\hat{A}(t_A) = \hat{A}(t_A)\hat{B}(t_B), &\text{if $\hat{A}$ is annihilation-like.} \end{cases} \end{equation*}\]So $\hat{A}^\bullet(t_A)\hat{B}^{\bullet}(t_B) = 0$.
∎
For the creation and destruction parts of the field operators we discussed earlier, they have the following anti-commutation relations:
\[\begin{align} & \qty[\hat{\psi}_{I\alpha}^{(1)}(x),\hat{\psi}_{I\beta}^{(2)}(x')]_+ = \qty[\hat{\psi}_{I\alpha}^{(1)\dagger}(x),\hat{\psi}_{I\beta}^{(2)\dagger}(x')]_+ = 0,\\[.2cm] & \qty[\hat{\psi}_{I\alpha}^{(1)\dagger}(x),\hat{\psi}_{I\beta}^{(2)}(x')]_+ = \qty[\hat{\psi}_{I\alpha}^{(1)}(x),\hat{\psi}_{I\beta}^{(2)\dagger}(x')]_+ =0,\\[.2cm] & \qty[\hat{\psi}_{I\alpha}^{(1)}(x),\hat{\psi}_{I\beta}^{(1)}(x')]_+ = \qty[\hat{\psi}_{I\alpha}^{(1)\dagger}(x),\hat{\psi}_{I\beta}^{(1)\dagger}(x')]_+ = 0, \\[.2cm] & \qty[\hat{\psi}_{I\alpha}^{(2)}(x),\hat{\psi}_{I\beta}^{(2)}(x')]_+ = \qty[\hat{\psi}_{I\alpha}^{(2)\dagger}(x),\hat{\psi}_{I\beta}^{(2)\dagger}(x')]_+ =0, \\[,2cm] & \qty[\hat{\psi}_{I\alpha}^{(1)}(x),\hat{\psi}_{I\beta}^{(1)\dagger}(x')]_+ = \frac{\delta_{\alpha\beta}}{V}\sum_{\vb{k}}\theta(\abs{\vb{k}}-k_F)\e^{i\vb{k}\cdot(\vb{x}-\vb{x}')- i\epsilon_{\vb{k}}^0(t-t')/\hbar}., \\[.2cm] & \qty[\hat{\psi}_{I\alpha}^{(2)}(x),\hat{\psi}_{I\beta}^{(2)\dagger}(x')]_+ = \frac{\delta_{\alpha\beta}}{V}\sum_{\vb{k}}\theta(k_F- \abs{\vb{k}})\e^{-i\vb{k}\cdot(\vb{x}-\vb{x}')+ i\epsilon_{\vb{k}}^0(t-t')/\hbar}. \end{align}\]Proof
We only prove the first and the fifth relations here. Others can be proved in the same way.
\[\begin{align*} \qty[\hat{\psi}_{I\alpha}^{(1)}(x),\hat{\psi}_{I\beta}^{(2)}(x')]_+ &= \frac{1}{V} \qty[\sum_{\abs{\vb{k}}>k_F} \hat{C}_{\vb{k}\alpha}\e^{i\vb{k}\cdot\vb{x}- i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}, \sum_{\abs{\vb{k}'}<k_F}\hat{C}_{\vb{k}'\beta}^\dagger\e^{-i\vb{k}'\cdot\vb{x}'+i\epsilon_{\vb{k}'}^0(t'-t_0)/\hbar}]_+\\[.2cm] & = \frac{1}{V} \sum_{\abs{\vb{k}}>k_F}\sum_{\abs{\vb{k}'}<k_F}\e^{i\vb{k}\cdot\vb{x}- i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}\e^{-i\vb{k}'\cdot\vb{x}'+i\epsilon_{\vb{k}'}^0(t'-t_0)/\hbar} \qty[\hat{C}_{\vb{k}\alpha},\hat{C}_{\vb{k}'\beta}^\dagger]_+\\[.2cm] & =0 . \end{align*}\]And
\[\begin{align*} \qty[\hat{\psi}_{I\alpha}^{(1)}(x),\hat{\psi}_{I\beta}^{(1)\dagger}(x')]_+ & = \frac{1}{V} \qty[\sum_{\abs{\vb{k}}>k_F} \hat{C}_{\vb{k}\alpha}\e^{i\vb{k}\cdot\vb{x}- i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}, \sum_{\abs{\vb{k}'}>k_F}\hat{C}_{\vb{k}'\beta}^\dagger\e^{-i\vb{k}'\cdot\vb{x}'+i\epsilon_{\vb{k}'}^0(t'-t_0)/\hbar}]_+ \\[.2cm] & = \frac{1}{V} \sum_{\abs{\vb{k}}>k_F}\sum_{\abs{\vb{k}'}> k_F} \e^{i\vb{k}\cdot\vb{x}- i\epsilon_{\vb{k}}^0(t-t_0)/\hbar}\e^{-i\vb{k}'\cdot\vb{x}'+i\epsilon_{\vb{k}'}^0(t'-t_0)/\hbar}\qty[\hat{C}_{\vb{k}\alpha},\hat{C}_{\vb{k}'\beta}^\dagger]_+ \\[.2cm] &=\frac{1}{V} \sum_{\abs{\vb{k}}>k_F}\e^{i\vb{k}\cdot(\vb{x}-\vb{x}')- i\epsilon_{\vb{k}}^0(t-t'/\hbar} \delta_{\alpha\beta} \\[.2cm] &= \frac{1}{V}\sum_{\vb{k}}\theta(\abs{k}-k_F)\e^{i\vb{k}\cdot(\vb{x}-\vb{x}')- i\epsilon_{\vb{k}}^0(t-t'/\hbar}\delta_{\alpha\beta}. \end{align*}\]∎
And their contractions are
\[\begin{align} &\hat{\psi}_{I\alpha}^{(1)\bullet}(x) \hat{\psi}_{I\beta}^{(2)\bullet}(x') =\hat{\psi}_{I\alpha}^{(1)\dagger\bullet}(x) \hat{\psi}_{I\beta}^{(2)\dagger\bullet}(x')= 0,\\[.2cm] & \hat{\psi}_{I\alpha}^{(1)\dagger\bullet}(x)\hat{\psi}_{I\beta}^{(2)\bullet}(x') = \hat{\psi}_{I\alpha}^{(1)\bullet}(x)\hat{\psi}_{I\beta}^{(2)\dagger\bullet}(x') =0,\\[.2cm] & \hat{\psi}_{I\alpha}^{(1)\bullet}(x)\hat{\psi}_{I\beta}^{(1)\bullet}(x') = \hat{\psi}_{I\alpha}^{(1)\dagger\bullet}(x)\hat{\psi}_{I\beta}^{(1)\dagger\bullet}(x') = 0, \\[.2cm] & \hat{\psi}_{I\alpha}^{(2)\bullet}(x)\hat{\psi}_{I\beta}^{(2)\bullet}(x') = \hat{\psi}_{I\alpha}^{(2)\dagger\bullet}(x)\hat{\psi}_{I\beta}^{(2)\dagger\bullet}(x') =0, \\[,2cm] &\hat{\psi}_{I\alpha}^{(1)\bullet}(x)\hat{\psi}_{I\beta}^{(1)\dagger\bullet}(x') = \theta(t - t') \frac{1}{V} \sum_{\vb{k}} \theta(\abs{\vb{k}}-k_F) \e^{i\vb{k}(\vb{x}-\vb{x}')-i\epsilon_{\vb{k}}^0(t - t')/\hbar},\\[.2cm] &\hat{\psi}_{I\alpha}^{(2)\bullet}(x)\hat{\psi}_{I\beta}^{(2)\dagger\bullet}(x') = \theta(t' - t) \frac{1}{V} \sum_{\vb{k}} \theta(k_F- \abs{\vb{k}}) \e^{-i\vb{k}(\vb{x}-\vb{x}')+i\epsilon_{\vb{k}}^0(t - t')/\hbar}. \end{align}\]Proof
The first four equations are trivial. We only prove the fifth equation here.
\[\begin{align*} \hat{\psi}^{(1)\bullet}_{I\alpha}(x) \hat{\psi}_{I\beta}^{(1)\dagger\bullet}(x') &= \hat{\mathsf{T}} \qty[\hat{\psi}^{(1)}_{I\alpha}(x) \hat{\psi}_{I\beta}^{(1)\dagger}(x')] - \hat{\mathsf{N}}\qty[\hat{\psi}^{(1)}_{I\alpha}(x) \hat{\psi}_{I\beta}^{(1)\dagger}(x')] \\[.2cm] & = \theta(t-t') \hat{\psi}^{(1)}_{I\alpha}(x) \hat{\psi}_{I\beta}^{(1)\dagger}(x') - \theta(t'-t)\hat{\psi}_{I\beta}^{(1)\dagger}(x') \hat{\psi}^{(1)}_{I\alpha}(x) + \hat{\psi}_{I\beta}^{(1)\dagger}(x') \hat{\psi}^{(1)}_{I\alpha}(x) \\[.2cm] & = \theta(t-t')\hat{\psi}^{(1)}_{I\alpha}(x) \hat{\psi}_{I\beta}^{(1)\dagger}(x') + \theta(t-t') \hat{\psi}_{I\beta}^{(1)\dagger}(x') \hat{\psi}^{(1)}_{I\alpha}(x)\\[.2cm] & = \theta(t-t') \qty[\hat{\psi}^{(1)}_{I\alpha}(x),\hat{\psi}_{I\beta}^{(1)\dagger}(x')]_+\\[.2cm] & = \theta(t-t')\frac{1}{V}\sum_{\vb{k}}\theta(\abs{k}-k_F)\e^{i\vb{k}\cdot(\vb{x}-\vb{x}')- i\epsilon_{\vb{k}}^0(t-t')/\hbar}\delta_{\alpha\beta} \end{align*}\]∎
So the contractions of field operators are
\[\begin{align} &\hat{\psi}_{I\alpha}^{\bullet}(x) \hat{\psi}^{\dagger\bullet}_{I\beta}(x') = -\hat{\psi}_{I\beta}^{\dagger\bullet}(x')\hat{\psi}_{I\alpha}^{\bullet}(x)= i G_{\alpha\beta}^0 (\vb{x},t;\vb{x}',t') := iG_{\alpha\beta}^0(x,x') \label{contraction}\\[.2cm] &\hat{\psi}_{I\alpha}^{\bullet}(x) \hat{\psi}_{I\beta}^\bullet(x') = \hat{\psi}_{I\alpha}^{\dagger\bullet}(x) \hat{\psi}_{I\beta}^{\dagger\bullet}(x') = 0. \end{align}\]Proof
We only proof the first equation.
\[\begin{align*} \hat{\psi}_{I\alpha}^{\bullet}(x) \hat{\psi}^{\dagger\bullet}_{I\beta}(x') & = \qty[\hat{\psi}_{I\alpha}^{(1)}(x) + \hat{\psi}_{I\alpha}^{(2)\dagger}(x)]^\bullet\qty[\hat{\psi}_{I\beta}^{(1)\dagger}(x') + \hat{\psi}_{I\beta}^{(2)}(x')]^\bullet\\[.2cm] & = \hat{\psi}_{I\alpha}^{(1)\bullet}(x)\hat{\psi}_{I\beta}^{(1)\dagger\bullet}(x') + \cancelto{0}{\hat{\psi}_{I\alpha}^{(1)\bullet}(x) \hat{\psi}_{I\beta}^{(2)\bullet}(x')} + \cancelto{0}{\hat{\psi}_{I\alpha}^{(2)\dagger\bullet}(x)\hat{\psi}_{I\beta}^{(1)\dagger\bullet}(x')} + \hat{\psi}_{I\alpha}^{(2)\dagger\bullet}(x)\hat{\psi}_{I\beta}^{(2)\bullet}(x')\\[.2cm] &= \theta(t - t') \frac{\delta_{\alpha\beta}}{V} \sum_{\vb{k}} \theta(\abs{\vb{k}}-k_F) \e^{i\vb{k}(\vb{x}-\vb{x}')-i\epsilon_{\vb{k}}^0(t_t')/\hbar} - \theta(t'-t) \frac{\delta_{\alpha\beta}}{V}\sum_{\vb{k}}\theta(k_F- \abs{k})\e^{i\vb{k}\cdot(\vb{x}-\vb{x}')- i\epsilon_{\vb{k}}^0(t-t')/\hbar}\\[.2cm] &=\frac{\delta_{\alpha\beta}}{V} \qty[\theta(t-t')\theta(\abs{\vb{k}}-k_F) - \theta(t'-t)\theta(k_F-\abs{\vb{k}})] \e^{i\vb{k}\cdot(\vb{x}-\vb{x}')- i\epsilon_{\vb{k}}^0(t-t')/\hbar}\\[.2cm] &=iG_{\alpha\beta}^0(\vb{x},t;\vb{x}',t'). \end{align*}\]∎
Note that the contractions are c numbers in the occupation-number Hilbert space, not operators. And $\eqref{contraction}$ can be simply derived with observation (another method)
\[\begin{align*} i G_{\alpha\beta}^0(x,x') &= \ev{\hat{\mathsf{T}}\qty[\hat{\psi}_{I\alpha}(x)\hat{\psi}_{I\beta}(x')]}{\Phi^0} \\[.2cm] &= \ev{ \hat{\psi}_{I\alpha}^{\bullet}(x) \hat{\psi}^{\dagger\bullet}_{I\beta}(x')}{\Phi^0} + \ev{\hat{\mathsf{N}}\qty[\hat{\psi}_{I\alpha}(x)\hat{\psi}_{I\beta}^\dagger(x')]}{\Phi^0}\\[.2cm] &= \hat{\psi}_{I\alpha}^{\bullet}(x) \hat{\psi}^{\dagger\bullet}_{I\beta}(x'). \end{align*}\]2.3. Wick’s theorem
Before our proof of the Wick’s theorem, we will introduce a basic lemma.
If $\hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots\hat{A}_n]$ is a normal-ordered product and $\hat{B}$ is a factor labeled with a time earlier than the times for $\hat{A}_1,\hat{A}_2,\cdots,\hat{A}_n$, i.e. $t_B < t_{A_1},t_{A_2},\dots, t_{A_n}$, then
\[\begin{equation} \begin{split} \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots \hat{A}_n] \hat{B} &=\hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots\hat{A}_{n-1}]\hat{A}_n^{\bullet}\hat{B}^{\bullet} - \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots \hat{A}_{n-2}\hat{A}_n]\hat{A}_{n-1}^{\bullet}\hat{B}^{\bullet} \\[.2cm] &+ \cdots+ (-1)^{n-1}\hat{\mathsf{N}}\qty[\hat{A}_2\cdots \hat{A}_{n-1}\hat{A}_n]\hat{A}_1^\bullet \hat{B}^\bullet + \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots\hat{A}_n\hat{B}]. \end{split} \label{lemma} \end{equation}\]Proof
If $\hat{B}$ is an annihilation like operator, then all the contractions vanish since $\hat{\mathsf{T}}\qty[\hat{A}_i\hat{B}] = \hat{\mathsf{N}}\qty[\hat{A}_i \hat{B}] = \hat{A}_i \hat{B}$. Thus, only the last term in $\eqref{lemma}$ contributes and the lemma is proved.
Then we just need to prove the case where $\hat{B}$ is a creation like operator. Without loss of generality, the operator product $\hat{A}_1\hat{A}_2\cdots \hat{A}_n$ can be assumed to be normal ordered, since otherwise the operators can be reordered on both sides of the equation. And we can further assume that $\hat{A}_n$ is a creation operator, and other operators $\hat{A}_i,(i\neq n)$ are all annihilation like operators. If the lemma is proved in this form, creation operators may be included by multiplyting on the left; the additional contractions so introduced vanish identically and can therefore be added to the right side of $\eqref{lemma}$ without changing the result.
The proof follows by induction. If $n=2$, the result is trivial:
\[\begin{align*} \mathrm{L.H.S} = \hat{\mathsf{N}}\qty[\hat{A}_1] \hat{B} = \hat{A}_1 \hat{B} = \hat{\mathsf{T}}\qty[\hat{A}_1\hat{B}] = \hat{A}_1^{\bullet}\hat{B}^{\bullet} - \hat{\mathsf{N}}\qty[\hat{A}_1 \hat{B}] = \mathrm{R.H.S}. \end{align*}\]We assume it is true for $n=m$, then we have
\[\begin{align*} \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots \hat{A}_m] \hat{B} &=\hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots\hat{A}_{m-1}]\hat{A}_m^{\bullet}\hat{B}^{\bullet} - \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots \hat{A}_{m-2}\hat{A}_m]\hat{A}_{m-1}^{\bullet}\hat{B}^{\bullet} \\[.2cm] &+ \cdots+ (-1)^{m-1}\, \hat{\mathsf{N}}\qty[\hat{A}_2\cdots \hat{A}_{m-1}\hat{A}_m]\hat{A}_1^\bullet \hat{B} + \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots\hat{A}_m\hat{B}]. \end{align*}\]For $n=m+1$, we have
\[\begin{align*} \hat{\mathsf{N}}\qty[\hat{A}\hat{A}_1\hat{A}_2\cdots \hat{A}_m]\hat{B} & = \hat{A} \, \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots \hat{A}_m] \hat{B}\\[.2cm] &=\textcolor{crimson}{\hat{\mathsf{N}}\qty[\hat{A}\hat{A}_1\hat{A}_2\cdots \hat{A}_{m-1}]\hat{A}_m^\bullet\hat{B}^\bullet - \hat{\mathsf{N}}\qty[\hat A\hat{A}_1\hat{A}_2 \cdots \hat{A}_{m-2}\hat{A}_m] \hat{A}_{m-1}^\bullet \hat{B}^\bullet} \\[.2cm] &\textcolor{crimson}{+ \cdots + (-1)^{m-1}\, \hat{\mathsf{N}}\qty[\hat{A}\hat{A}_2\cdots \hat{A}_m]\hat{A}_1^\bullet \hat{B}^{\bullet}} + \hat{A}\,\hat{\mathsf{N}}\qty[\hat{A}_1 \hat{A}_2 \cdots \hat{A}_m\hat{B}]. \end{align*}\]We want to reach the result
\[\begin{align*} \hat{\mathsf{N}}\qty[\hat{A}\hat{A}_1\hat{A}_2\cdots \hat{A}_m]\hat{B} &\overset{?}{=} \textcolor{crimson}{\hat{\mathsf{N}}\qty[\hat{A}\hat{A}_1\hat{A}_2\cdots \hat{A}_{m-1}]\hat{A}_m^{\bullet}\hat{B}^{\bullet} - \hat{\mathsf{N}}\qty[\hat{A}\hat{A}_1\hat{A}_2\cdots \hat{A}_{m-2}\hat{A}_m]\hat{A}_{m-1}^{\bullet}\hat{B}^{\bullet}}\\[.2cm] &\textcolor{crimson}{+\cdots + (-1)^{m-1}\, \hat{\mathsf{N}}\qty[\hat{A}\hat{A}_2\cdots \hat{A}_m] \hat{A}_1^\bullet \hat{B}^\bullet} + (-1)^m\, \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots \hat{A}_m] \hat{A}^{\bullet}\hat{B}^{\bullet}\\[.2cm] & + \hat{\mathsf{N}}\qty[\hat{A}\hat{A}_1\hat{A}_2\cdots \hat{A}_m\hat{B}]. \end{align*}\]The red parts in these two equations are the same. So we only need to prove
\[\begin{align*} \hat{A}\,\hat{\mathsf{N}}\qty[\hat{A}_1 \hat{A}_2 \cdots \hat{A}_m\hat{B}] \overset{?}{=}(-1)^m \, \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\cdots \hat{A}_m] \hat{A}^{\bullet}\hat{B}^{\bullet}+ \hat{\mathsf{N}}\qty[\hat{A}\hat{A}_1\hat{A}_2\cdots \hat{A}_m\hat{B}]. \end{align*}\]This can be proved directly
\[\begin{align*} \mathrm{L.H.S} &= (-1)^m \hat{A}\hat{B}\, \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2 \cdots \hat{A}_m]\\[.2cm] &= (-1)^m \hat{A}\hat{B}\hat{A}_1\hat{A}_2 \cdots \hat{A}_m\\[.2cm] &= (-1)^m\, \hat{\mathsf{T}}\qty[\hat{A}\hat{B}] \hat{A}_1\hat{A}_2 \cdots \hat{A}_m \\[.2cm] &= (-1)^m \qty(\hat{A}^\bullet\hat{B}^{\bullet} + \hat{\mathsf{N}}\qty[\hat{A}\hat{B}]) \hat{A}_1\hat{A}_2 \cdots \hat{A}_m\\[.2cm] &= (-1)^m \hat{A}_1 \hat{A}_2 \cdots \hat{A}_m \hat{A}^\bullet\hat{B}^{\bullet} + (-1)^m\, \hat{\mathsf{N}}\qty[\hat{A}\hat{B}]\hat{A}_1\hat{A}_2 \cdots \hat{A}_m \\[.2cm] &=(-1)^m\, \hat{\mathsf{N}}\qty[\hat{A}_1 \hat{A}_2 \cdots \hat{A}_m]\hat{A}^\bullet\hat{B}^{\bullet} + (-1)^{m+1}\, \hat{\mathsf{N}}\qty[\hat{B}\hat{A}]\hat{A}_1\hat{A}_2 \cdots \hat{A}_m \\[.2cm] &=(-1)^m\, \hat{\mathsf{N}}\qty[\hat{A}_1 \hat{A}_2 \cdots \hat{A}_m]\hat{A}^\bullet\hat{B}^{\bullet} + (-1)^{m+1}\, \hat{\mathsf{N}}\qty[\hat{B}\hat{A}\hat{A}_1 \cdots \hat{A}_m]\\[.2cm] &= (-1)^m\, \hat{\mathsf{N}}\qty[\hat{A}_1 \hat{A}_2 \cdots \hat{A}_m]\hat{A}^\bullet\hat{B}^{\bullet} + (-1)^{m+1}(-1)^{m+1}\, \hat{\mathsf{N}}\qty[\hat{A}\hat{A}_1 +\cdots \hat{A}_m \hat{B}]\\[.2cm] &=(-1)^m\, \hat{\mathsf{N}}\qty[\hat{A}_1 \hat{A}_2 \cdots \hat{A}_m]\hat{A}^\bullet\hat{B}^{\bullet} + \hat{\mathsf{N}}\qty[\hat{A}\hat{A}_1 +\cdots \hat{A}_m \hat{B}]\\[.2cm] &=\mathrm{R.H.S.} \end{align*}\]So this lemma is indeed true for $n=m+1$. Then we have proved this basic lemma.
∎
Thus if a normal-ordered product is multiplied on the right with any operator at an earlier time, we obtain a sum of normal-ordered products containing the extra operator contracted in turn with all the operators standing in the original product, along with a term where the extra operator is included within the normal-ordered product.
As an example, we write a case of $n=4$ explicitly:
\[\begin{align*} \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\hat{A}_3\hat{A}_4]\hat{B} & = \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2\hat{A}_3]\hat{A}_4^\bullet\hat{B}^{\bullet} - \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2 \hat{A}_4]\hat{A}_3^\bullet\hat{B}^{\bullet} + \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_3 \hat{A}_4]\hat{A}_2^\bullet\hat{B}^{\bullet} \\[.2cm] & \quad - \hat{\mathsf{N}}\qty[\hat{A}_2\hat{A}_3 \hat{A}_4]\hat{A}_1^\bullet\hat{B}^{\bullet} + \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2 \hat{A}_3\hat{A}_4\hat{B}] \end{align*}\]The time ordering of $\hat{A}_1\hat{A}_2\cdots \hat{A}_n$ can be expressed through contractions of some pair operators, while the remaining operators yield the normal-ordered product, and then take sum of all the possible choices.
\[\begin{equation} \begin{split} &\hat{\mathsf{T}}\qty[\hat{A}_1\hat{A}_2 \cdots \hat{A}_n]\\[.2cm] ={}& \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2 \cdots\hat{A}_n] \\[.2cm] &{}+ \sum_{i<j}(-1)^P \hat{A}_i^\bullet\hat{A}_j^\bullet\, \hat{\mathsf{N}}\qty[\hat{A}_1 \cdots i \cdots j\cdots \hat{A}_n]\\[.2cm] & {}+ \sum_{i<j}\sum_{k<l} (-1)^P \hat{A}_i^\bullet\hat{A}_j^\bullet \hat{A}_k^{\bullet\bullet}\hat{A}_l^{\bullet\bullet}\, \hat{\mathsf{N}}\qty[\hat{A}_1 \cdots i \cdots j \cdots k \cdots l\cdots \hat{A}_n ]\\[.2cm] & + \cdots + \sum _{i<j}\sum_{k<l} \cdots \sum \hat{A}_i^\bullet\hat{A}_j^\bullet \hat{A}_k^{\bullet\bullet}\hat{A}_l^{\bullet\bullet} \cdots \\[.2cm] ={}& \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2 \cdots\hat{A}_n] + \hat{\mathsf{N}}\qty[\text{sum over all possible pairs of contractions}]. \end{split} \end{equation}\]where $P$ is the number of interchanges of fermion operators from the original given order.
Proof
Again the theorem will be proved by induction. It is obviously true for $n=2$,
\[\hat{\mathsf{T}}\qty[\hat{A}_1\hat{A}_2] = \hat{\mathsf{N}}\qty[\hat{N}_1\hat{N}_2] + \hat{A}_1^\bullet\hat{A}_2^\bullet.\]Assume it is true for $n=m$, and multiply on the right by an operator $\hat{B}$ with a time earlier than that of any other operators (i.e., $t_B < t_{A_1},t_{A_2},\dots, t_{A_m}$).
\[\begin{align*} \hat{\mathsf{T}}\qty[\hat{A}_1\cdots \hat{A}_m \hat{B}]& =\hat{\mathsf{T}}\qty[\hat{A}_1\cdots\hat{A}_{m-1}\hat{A}_m]\hat{B} \\[.2cm] &=\hat{\mathsf{N}}\qty[\hat{A}_1\cdots \hat{A}_{m-1}\hat{A}_m]\hat{B} + \hat{\mathsf{N}}\qty[\hat{A}_1^\bullet\hat{A}_2^\bullet\hat{A}_3\cdots \hat{A}_{m-1}\hat{A}_m]\hat{B} + \cdots\\[.2cm] &=\hat{\mathsf{N}}\qty[\hat{A}_1\cdots\hat{A}_{m-1}\hat{A}_m \hat{B}] + \hat{\mathsf{N}}\qty[\text{sum over all possible pairs of contractions}]. \end{align*}\]Note that on the right side, we use the basic lemma $\eqref{lemma}$ to introduce the operator $\hat{B}$ into the normal-ordered products. The restriction on the time of the operator $\hat{B}$ can now be removed by simultaneously reordering the operators in each term of the above equation. Then we have proved the Wick’s theorem.
∎
Maybe Wick’s theorem looks a little complicated, but let’s write down the case where $n=4$ explicitly.
\[\begin{align*} \hat{\mathsf{T}}\qty[\hat{A}_1\hat{A}_2\hat{A}_3\hat{A}_4] & = \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2 \hat{A}_3 \hat{A}_4] + \hat{A}_1^\bullet\hat{A}_2^\bullet\, \hat{\mathsf{N}}\qty[\hat{A}_3\hat{A}_4] - \hat{A}_1^\bullet\hat{A}_3^\bullet\, \hat{\mathsf{N}}\qty[\hat{A}_2\hat{A}_4]\\[.2cm] &\quad + \hat{A}_1^\bullet\hat{A}_4^\bullet\, \hat{\mathsf{N}}\qty[\hat{A}_2\hat{A}_3] + \hat{A}_2^\bullet\hat{A}_3^\bullet\, \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_4] - \hat{A}_2^\bullet\hat{A}_4^\bullet\, \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_3]\\[.2cm] &\quad + \hat{A}_3^\bullet\hat{A}_4^\bullet\, \hat{\mathsf{N}}\qty[\hat{A}_1\hat{A}_2] + \hat{A}_1^\bullet\hat{A}_2^\bullet \hat{A}_3^{\bullet\bullet}\hat{A}_4^{\bullet\bullet} - \hat{A}_1^\bullet\hat{A}_3^\bullet \hat{A}_2^{\bullet\bullet}\hat{A}_4^{\bullet\bullet}\\[.2cm] & \quad+ \hat{A}_1^\bullet\hat{A}_4^\bullet \hat{A}_2^{\bullet\bullet}\hat{A}_3^{\bullet\bullet}. \end{align*}\]Note that we only discuss the case where all operators are either creation or destruction parts of the field. The $\hat{\mathsf{T}}$ product and the $\hat{\mathsf{N}}$ product are both distributive, however, and Wick’s theorem thus applies to the fields themselves.
By Wick’s theorem, the time-ordered product can transformed to sum of all possible contractions and normal-ordered product. Only the expectation value in the noninteracting ground state of full contractions not equal to zero. So $\eqref{green-function-expansion}$ can be expressed in a series containing $U$ and $G^0$ that can be solved exactly.
3. References
- Fetter, A. L., Walecka, J. D., Quantum Theory of Many-Particle Systems. Courier Corporation. (2002)
- Mahan, G. D., Many-Particle Physics. Springer Science+Business Media, LLC. (2000).
- Altland, A., Simons, B. D., Condensed Matter Field Theory. Cambridge University Press. (2010)
- 金彪. 量子多体理论. 2024年春